本质
贝塞尔函数的本质就是通过一种数学的方式来抽象某些运动模式，比如 先快后慢，先慢后快，中间快两边慢，也可以用来描述匀速运动。
因为其曲线变化的特性，如果将横轴看作时间，纵轴看作路程，将上面每点的切线斜率作为 速度，那么随着时间的推移，其速度变化是很均匀的，不管是增加或者减少都会有一个平稳的过渡，这也是为什么很多领域用贝塞尔曲线来拟合动效表现，给人感官上的舒适。
H5 应用
如果用 css 做不太复杂的动效，那么一般定义首尾两帧，中间加个动效函数就绰绰有余了。
也就是两帧用 transition，多帧用 animation，整个动画的延迟，持续时间等等都可以快速定义，其中最精髓的就数 transition-timing-function 了，用不同的缓动函数，动效表现上可能出现很大区别，这些细节直接影响到产品的整体表现。
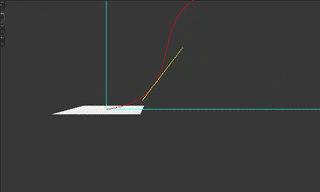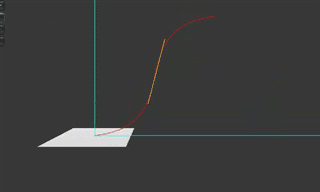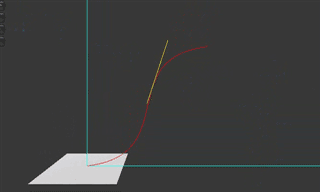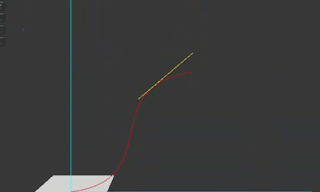
transition 中提供了 cubic-bezier 函数用来快速定义一个贝塞尔函数，即类似 cubic-bezier(x1,y1,x2,y2) 的写法，其中 (x1,y1) ，（x2,y2) 分别表示两个二维向量的终点坐标，借用动图表示如下：
图中 O 表示原点 (0,0), E 表示单位坐标系中的 (1,1), A 的坐标即为 (x1,y1), B 的坐标即为 (x2,y2)。
向量 OA 和 EB 定义了这条贝塞尔曲线的起点和终点的切线方向，即开始的发射方向和结束的进入方向，上面这条曲线描述了一个简单的运动过程：先快后慢。
我们可以从切线的斜率变化上感受到：
上面说的运动过程其实是个比较抽象的概念，一个人跑步可以是运动过程，动画变化也是运动过程，比如一个动画有开始帧和结束帧，在中间均匀插入过渡的帧，那么就是前面的帧放的速度比较快，后面的帧播放速度比较慢，人的感官可以很容易捕捉到这种差异。
在 transition 中如果每次都要精准定义两个向量来表示这一过程，其实是麻烦的，所以 css 提供了 ease-out 来粗略表示上面一个由快到慢的过程，但是发现好的 cubic-bezier 函数肯定是要收藏的，因为和 ease-out 的表现在各种动效表现上差异还是很大的。
由此我们可以顺理成章描述一个先慢后快的过程：
上述过程其实用一阶贝塞尔函数也能描述，即中间两个向量其实是一个位置：(x1,y1) 和 (x2,y2) 表示同一个点。
也就是说高阶的贝塞尔函数一定能表示低阶贝塞尔函数，所有低阶的贝塞尔函数都是高阶贝塞尔函数的特例，首尾中间有几个点就是几阶贝塞尔函数，因此理论上任何平滑的非封闭曲线都可以用贝塞尔函数表示，这也是为什么 PS 的钢笔工具可以用来抠图的原因。
下面是一二阶贝塞尔函数的计算公式：
一阶：B(t) = (1-t) * P0 + tP1 , 0 <= t <= 1;
二阶：B(t) = (1-t)^2*P0 + 2 *(1-t) *t*P1 + t^2*P2 , 0 <= t <= 1;
css 中还有一种特别常用的写在 transition 中的缓动函数：ease-in-out。
根据上面命名规律的特点很容易知道是表示先慢到快，由快到慢，即两边慢，中间快。这个缓动函数比较常用，很容易制造一种 Q弹 的效果。
基本上只要让定义的第一个坐标在右下方第四象限，第二个坐标在左上方第二象限，就可以自定义一个这种类型的缓动函数：
