DS博客作业—栈和队列
0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
·栈只能从表的一端存取数据,另一端是封闭的。
·在栈中,无论是存数据还是取数据,都必须遵循"先进后出"的原则,即最先进栈的
元素最后出栈。
定义:
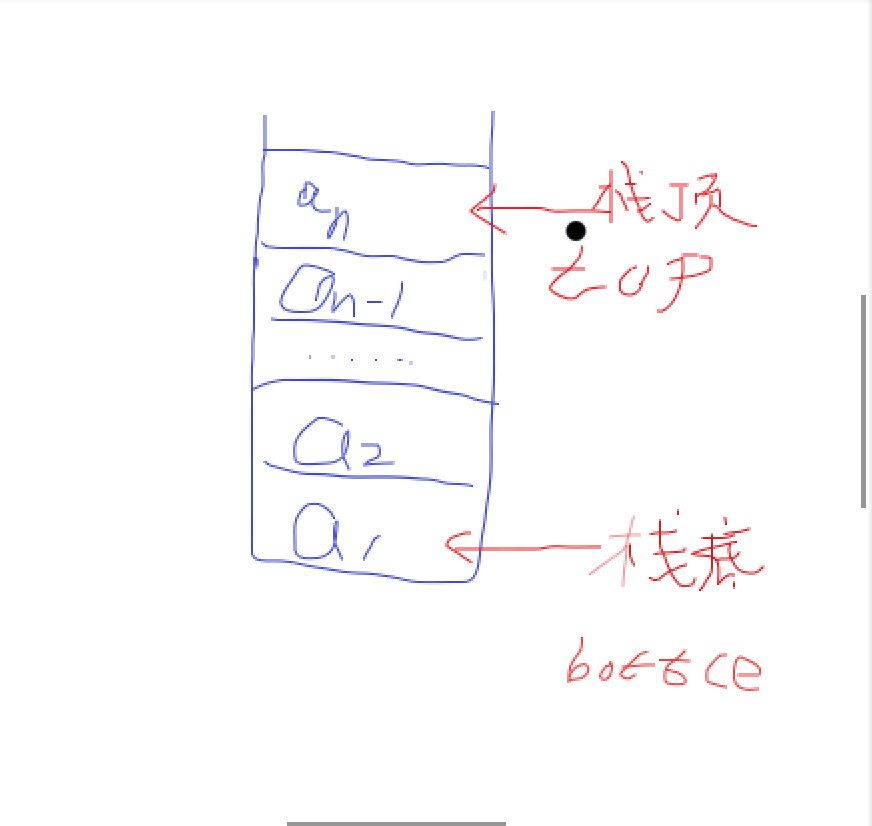
栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。
通常,栈的开口端被称为栈顶;相应地,封口端被称为栈底。因此,栈顶元素指的
就是距离栈顶最近的元素。
栈的实现
栈的具体实现有以下两种方式:
·顺序栈:采用顺序存储结构可以模拟栈存储数据的特点,从而实现栈存储构;
·链栈:采用链式存储结构实现栈结构;
区别:
·两种实现方式的区别,仅限于数据元素在实际物理空间上存放的相对位置,顺序栈
底层采用的是数组,链栈底层采用的是链表。有关顺序栈和链栈的具体实现会在
后续章节中作详细讲解。
对于一个栈,栈的长度为5,则:
普通栈
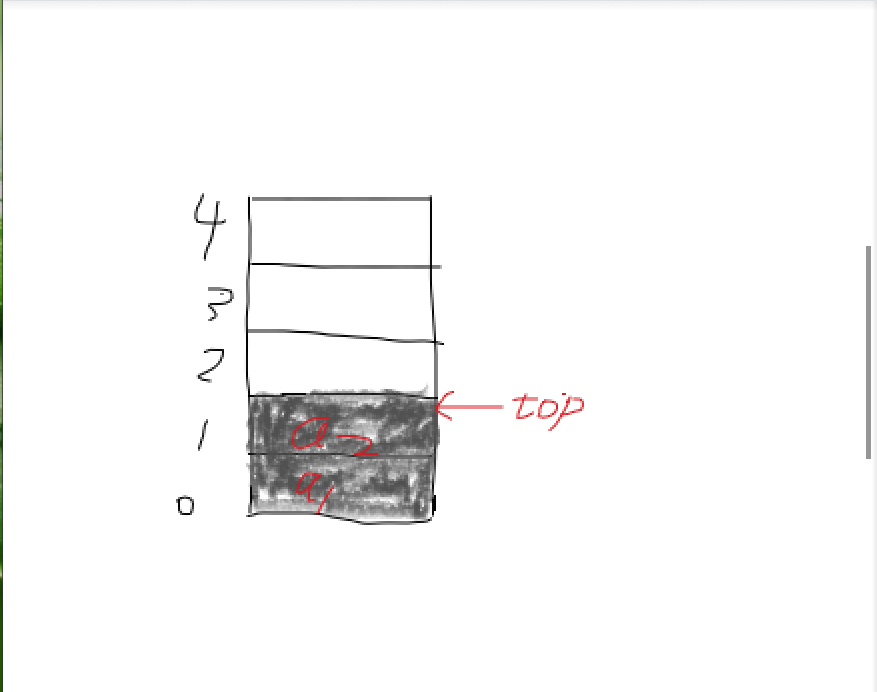
栈有两个元素,top=1
栈满
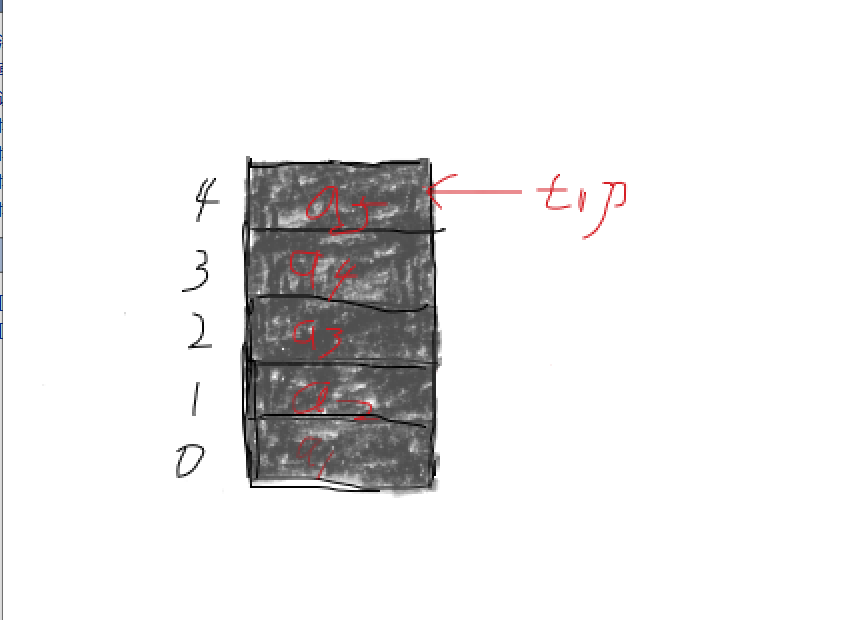
栈中有5个元素,top=4;
栈空
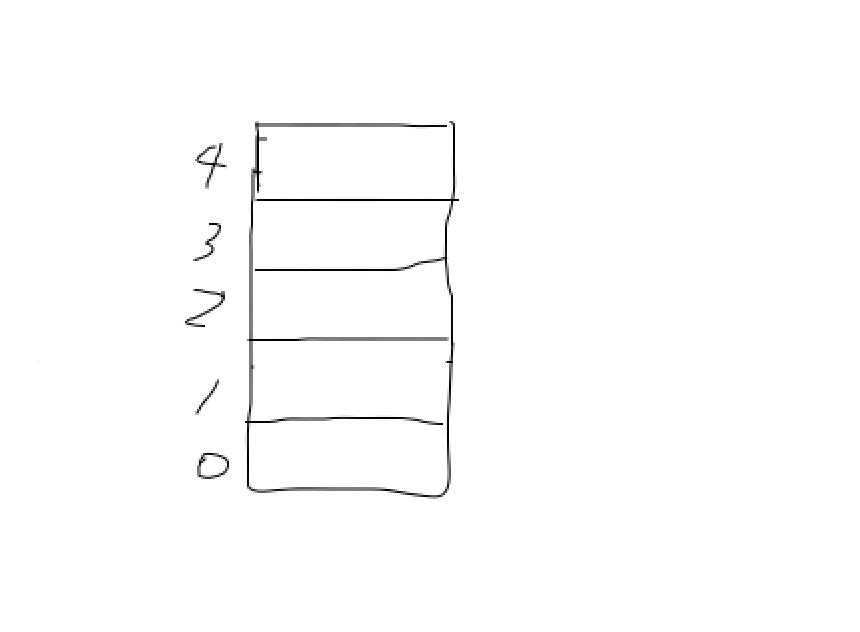
栈中为空,top=-1
栈的应用
·基于栈结构对数据存取采用 "先进后出" 原则的特点,它可以用于实现很多功能。
·例如,我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A,然后关
闭了页面 A 跳转到页面 B,随后又关闭页面 B 跳转到了页面 C。而此时,我们
如果想重新回到页面 A,有两个选择:
·重新搜索找到页面 A;
·使用浏览器的"回退"功能。浏览器会先回退到页面 B,而后再回退到页面 A。
·浏览器 "回退" 功能的实现,底层使用的就是栈存储结构。当你关闭页面 A 时,浏
览器会将页面 A 入栈;同样,当你关闭页面 B 时,浏览器也会将 B入栈。因此,当
你执行回退操作时,才会首先看到的是页面 B,然后是页面 A,这是栈中数据依次出
栈的效果。
·不仅如此,栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用
到括号(小括号、中括号和大括号),括号的错误使用(通常是丢右括号)会导致程序
编译错误,而很多开发工具中都有检测代码是否有编辑错误的功能,其中就包含检测代
码中的括号匹配问题,此功能的底层实现使用的就是栈结构。
顺序栈

·栈分为顺序栈和链栈。
·顺序栈用数组存数据,整型指向栈顶。
·特点就是先入先出原则。
·栈在逻辑上是线性结构。
链式储存结构(链栈)
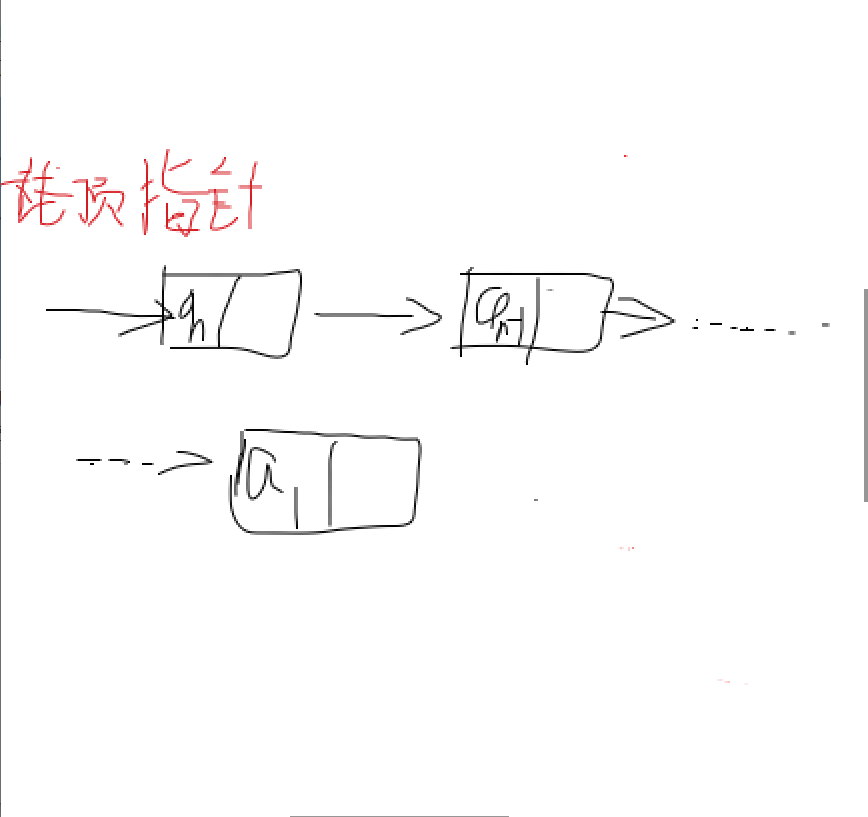
栈的链式存储结构,简称链栈。
由于栈只是栈顶在做插入和删除操作,所以栈顶应该放在单链表的头部。另外,都有了栈顶
在头部了,单链表中的头结点也就失去了意义,通常对于链栈来说,是不需要头结点的。
对于链栈来说,基本不存在栈满的情况,除非内存已经没有使用空间了。
对于空栈来说,链表原来的定义是头指针指向空,那么链栈的空其实就是top=NULL
栈的结构体定义
typedef struct StackNode
{
int data;//结点数据域
struct StackNode* next;//结点指针域
}StackNode,* Linktop; //链栈的数据结构
typedef struct LinkStack
{
Linktop top; //栈顶结点,定义了一个指向上个结构体的指针
int count;//元素个数
}LinkStack;
进栈操作
int push(LinkStack& stack,int e)
{
if (!stack)
{
return 0;
}
LinkStack node = new StackNode;
node->next = stack->top;//将元素加入链表中
node->data = e;
stack->top = node;//栈顶元素指向压入元素
stack->count++;
return ture;
}
出栈操作
int pop(LinkStack& stack,int e)
{
if (!stack && stack->count)
{
return 0;
}
StackNode node = stack->top;
e = node->data;
stack->top = node->next; //栈顶指针指向新的栈顶元素
stack->count;
cout--;
}
队列
队列的定义:
·队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,
而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进
行插入操作的端称为队尾,进行删除操作的端称为队头。
·队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除
一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以只有最早进
入队列的元素才能最先从队列中删除,故队列又称为先进先出线性表。
队列的分类
·顺序队列
·循环队列
队列的链式存储结构及实现
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾进头出而已
,称之为链队列。
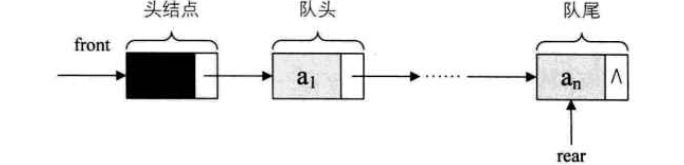
队头指针指向链队列的头结点,将队尾指针指向终端结点
当队列为空时,头指针指向尾指针

链队列的结构体:
typedef struct QNode //结点结构
{
QElemType data;
struct QNode *next;
}QNode, *QueuePtr;
typedef struct//队列的链表结构
{
QueuePtr front,rear; //队头队尾指针
}LinkQueue;
链队列的入队操作:

int EnQueue (LinkQueue &Q, QElemType e)
{
QueuePtr s =new QNode;//申请空间
s->data = e;
s->next = NULL;
Q->rear->next = s;// 把新结点s赋值给原队尾结点的后继
Q->rear = s;// 把当前的s设为队尾结点,rear指向s
return OK;
}
链队列的出队:
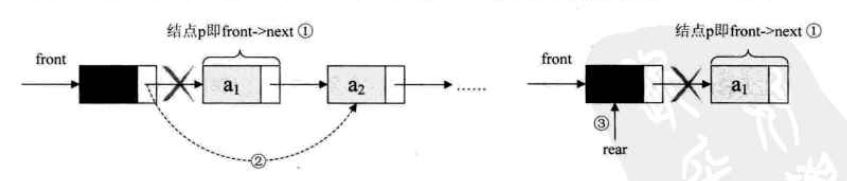
int DeQueue(LinkQueue &Q, QElemType e)
{
QueuePtr p;
if(Q->front == Q->rear)
{
return ERROR;
}
p = Q->front->next; //将欲删除的队头结点暂存给p
e = p->data; //将欲删除的队头结点的值赋给e
Q->front->next = p->next; //将原结点后继赋给头结点后继
if(Q->rear == p) //若队头是队尾,则删除后将rear指向头结点
{
Q->rear = Q->front;
}
return OK;
}
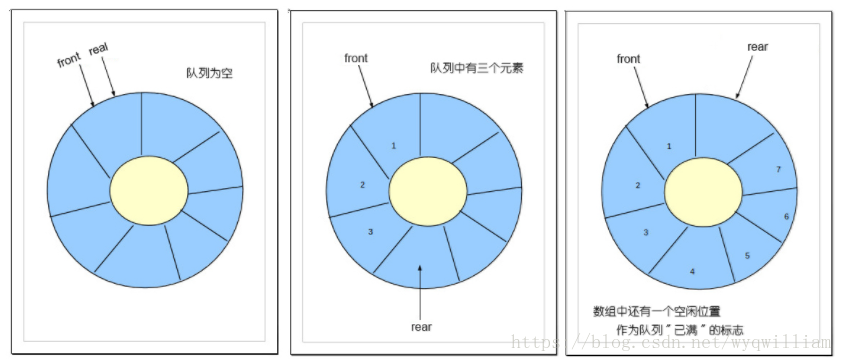
循环队列
假设是长度为5的数组,初始状态,空队列如所示,front与 rear指针均指向下标为0的位置。
然后入队a1、a2、a3、a4, front指针依然指向下标为0位置,而rear指针指向下标为4的位置。

假设是长度为5的数组,初始状态,空队列如所示,front与 rear指针均指向下标为0的位置。然后入队a1、a2、a3、a4, front指针依然指向下标为0位置,而rear指针指向下标为4的位置。
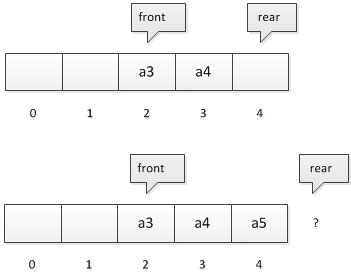
为了解决这个问题,引入了循环队列的概念
为了方便起见,初始化建空队时,
令:front=rear=0,
当队空时:front=rear
当队满时:front=rear 亦成立
因此只凭等式front=rear无法判断队空还是队满。 有两种方法处理上述问题:
(1)增加一个标识flag ,初始的时置为false,每当有元素入队时让flag = true,每当有元
素出队时,让flag = false,在触发rear = front 的上一个操作决定了是空还是满。这
样在判断空的时候 ,要判断 front == rear 和 flag 为假要同时成立,即( front ==
rear ) && !front 整体为真时,队列空。( front == rear ) && front 时 队列满
(2)增加一个引用计数count;
(3)少用一个元素空间,约定以“队列头指针front在队尾指针rear的下一个位置上”作为队列“满”状态的标志。即:
队空时: front=rear
队满时: (rear+1)%maxsize=front
循环队列的结构体定义
typedef struct
{
ElemType *base; //存储内存分配基地址
int front; //队列头索引
int rear; //队列尾索引
}circularQueue;
循环队列的入队列操作
int InsertQueue(circularQueue &q, ElemType e)
{
if ((q->rear + 1) % MAXSIZE == q->front) return; //队列已满时,不执行入队操作
q->base[q->rear] = e; //将元素放入队列尾部
q->rear = (q->rear + 1) % MAXSIZE; //尾部元素指向下一个空间位置,取模运算保证了索引不越界(余数一定小于除数)
}
循环队列的出队操作
DeleteQueue(circularQueue &q, ElemType &e)
{
if (q->front == q->rear) return; //空队列,直接返回
e = q->base[q->front]; //头部元素出队
q->front = (q->front + 1) % MAXSIZE;
}
2.PTA实验作业
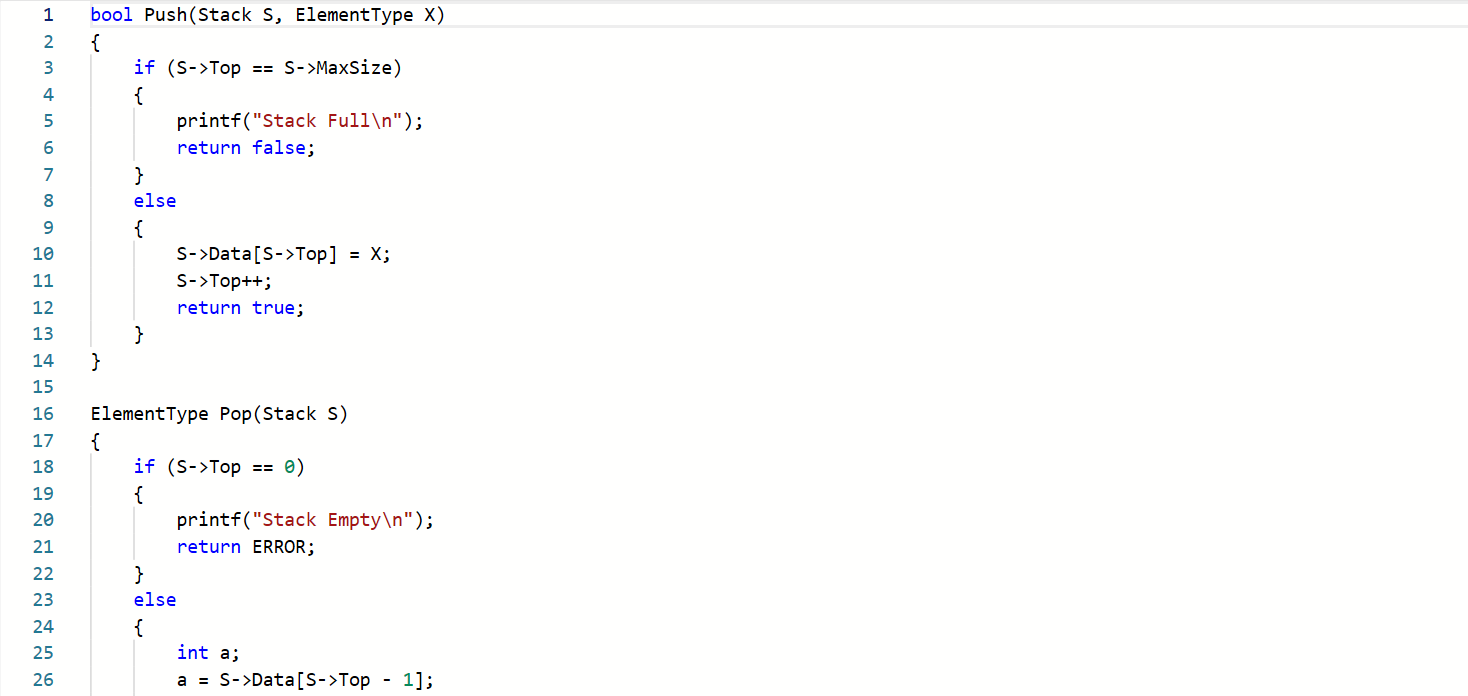
2.6-1 另类堆栈
伪代码简要介绍设计思路
进栈
判断栈是否满
if(满)then 返回错误
else
将数字赋给data的top位置
top++
返回正确
出栈
判断栈是否为空
if(空)then 返回错误
else
将数值赋给data的top位置
top--
返回数值

提交列表

·一开始top为0,所以进栈时,应该先赋值在自增,然后出栈时,因为进栈时,自增了一次,所以
出栈的元素应该是top-1,而不是出栈top所在的元素,然后再那top自减,这样就可以正确了
·出现了部分正确,错的测试点是格式错误
·忘记加\n了!!
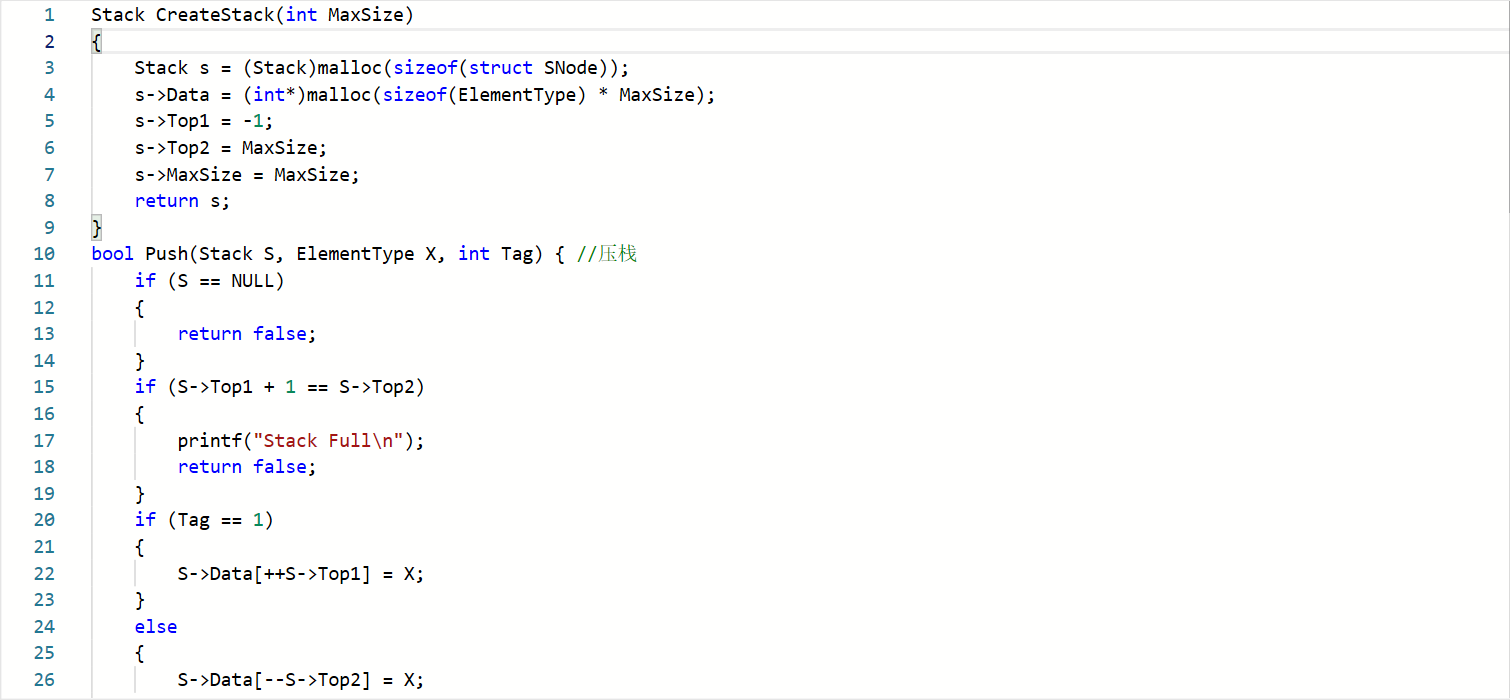
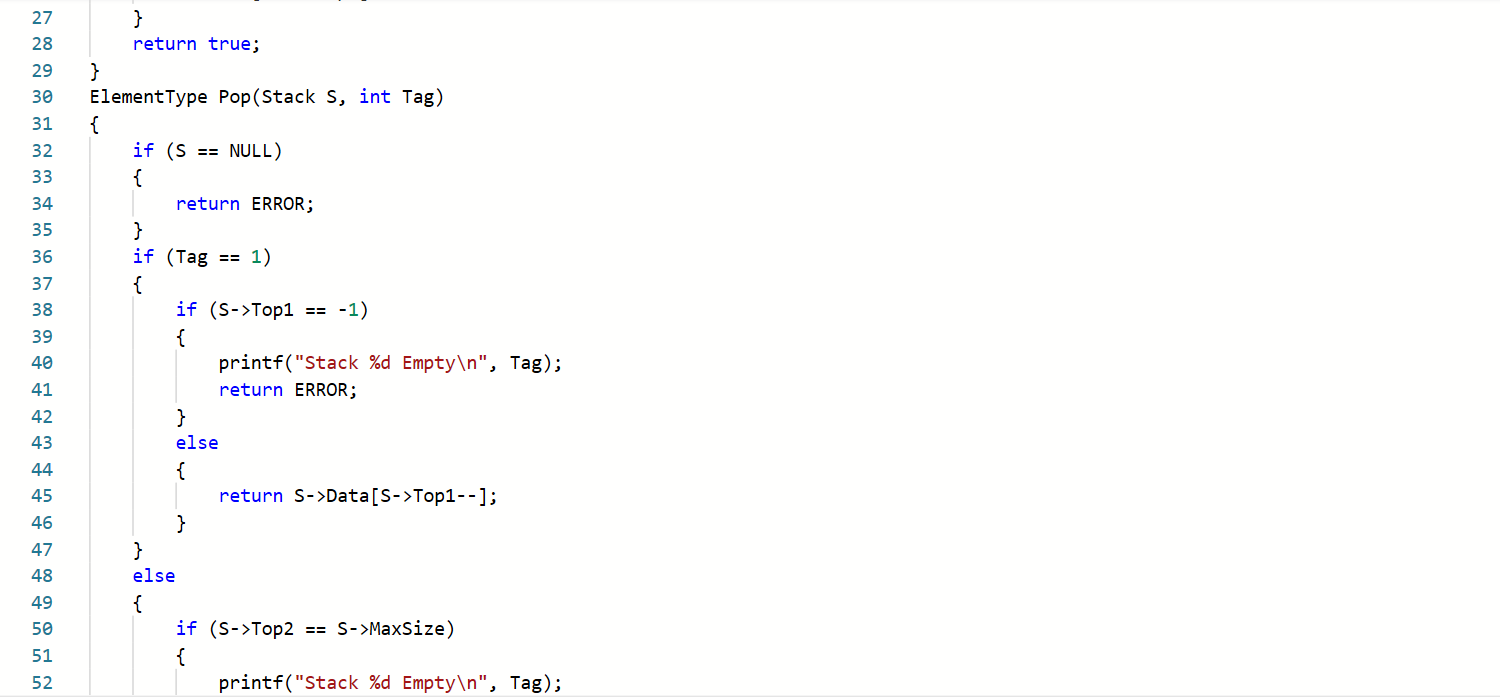
在一个数组中实现两个堆栈
伪代码简要介绍设计思路
动态申请空间
进栈
判断栈是否为空
If(空)
Return false
判断栈是否为满
If(满)
Return false
将元素储存到栈1或栈2中
出栈
判断栈是否为空
If(空)
Return ERROR
If(栈1)
If(空)
输出 Tag Empty Tag Empty
Else
出栈
If(栈2)
If(空)
输出 Tag Empty Tag Empty
Else
出栈

提交列表

·刚开始代码申请空间错误
·将Top1指向数组头,将Top2数组的尾
·在入栈操作后要进行S++操作
代码阅读
验证栈序列

思路
将入栈序列的每个元素入栈,如果栈顶元素等于出栈序列当前poped[i]元素,
则弹出栈元素并移动出栈序列(++i),最后如果栈为空,则有效。
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true

输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false

代码

该题的伪代码
定义两个iterator访问pushed和popped容器,用于读取元素,并且判断匹配成功标准
auto pushIt=pushed.begin();
循环(popped没有访问完时)
{
入栈操作: data为空或者data.top!=*popIt时:
{
1.1 有数可以入:pushIt!=pushed.end() :
{
data.push(*pushIt);
pushIt++;
}
1.2 否则无数可入: break;
}
否则出栈:
{
data.pop();
popIt++:
}
}
匹配成功条件:stack为空,且popIt访问到了popped.end()
运行

时间复杂度:O(n)
空间复杂度:O(n)
最小栈

思路
·两个栈,左边栈接受元素,右边栈存最小的元素
·入栈时,先入左边栈,随后进行比较,左边和右边栈顶元素进行比较,如果新元素小,就把新
元素放在右边的栈顶位置,如果新元素大,则还是把右边栈顶元素放在栈顶的位置
·出栈时,出的是最后一个入栈元素,所以就是左边的栈出栈
·出最小值时,就是右边的栈顶元素出栈
·出栈时两个都得出
代码





 浙公网安备 33010602011771号
浙公网安备 33010602011771号