MIT自然语言处理第五讲：最大熵和对数线性模型（第四部分）

自然语言处理：最大熵和对数线性模型
Natural Language Processing: Maximum Entropy and Log-linear Models 
作者：Regina Barzilay（MIT,EECS Department, October 1, 2004)
译者：我爱自然语言处理（www.52nlp.cn ，2009年5月9日）

三、 最大熵模型详述
c) 相对熵（Kullback-Liebler距离）（Relative Entropy (Kullback-Liebler Distance)）
　i. 定义（Definition）：两个概率分布p和q的相对熵D由下式给出（The relative entropy D between two probability distributions p and q is given by）
　　　　　　
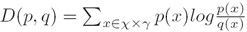
　ii. 引理1（Lemma 1）：对于任意两个概率分布p和q，D(p, q)≥0 且 D(p, q)=0 当且仅当p=q（For any two probability distributions p and q, D(p, q)≥ 0, and D(p, q)=0 if and only if p =q）
　iii. 引理2（毕达哥拉斯性质）（Lemma 2 (Pythagorean Property)）：若p∈P，q∈Q，p*∈P∩Q，则D(p, q) = D(p, p*) + D(p*, q) （If p ∈P and q ∈ Q, and p*∈P∩Q, then D(p, q) = D(p, p*) + D(p*, q)）
　注：证明请参看MIT NLP 的lec5.pdf英文讲稿；
d) 最大熵解（The Maximum Entropy Solution）
　i. 定理1(Theorem 1)：若p*∈P∩Q，则p* =  ,且p*唯一(If p∗∈P ∩Q then p* = . Furthermore, p* is unique)
注：证明请参看min nlp原讲稿，主要运用引理1和引理2得出。
e) 最大似然解（The Maximum Likelihood Solution）
　i. 定理2(Theorem 2)：若p*∈P∩Q，则p* =  ,且p*唯一(If p∗∈P ∩Q then p* = . Furthermore, p* is unique)
注：证明请参看min nlp原讲稿，主要运用引理1和引理2得出。
f) 对偶定理（Duality Theorem）
　i. 存在一个唯一分布p*(There is a unique distribution p*）
　　1. p*∈ P ∩ Q
　　2. p* =  (最大熵解（Max-ent solution）)
　　3. p* =  (最大似然解（Max-likelihood solution）)
　ii. 结论（Implications）：
　　1. 最大熵解可以写成对数线性形式（The maximum entropy solution can be written in log-linear form）
　　2. 求出最大似然解同样给出了最大熵解（Finding the maximum-likelihood solution also gives the maximum entropy solution）

未完待续…

附：课程及课件pdf下载MIT英文网页地址：
　　　http://people.csail.mit.edu/regina/6881/

注：本文遵照麻省理工学院开放式课程创作共享规范翻译发布，转载请注明出处“我爱自然语言处理”：www.52nlp.cn

本文链接地址：http://www.52nlp.cn/mit-nlp-fifth-lesson-maximum-entropy-and-log-linear-models-fourth-part/