MIT自然语言处理第五讲：最大熵和对数线性模型（第三部分）

自然语言处理：最大熵和对数线性模型
Natural Language Processing: Maximum Entropy and Log-linear Models 
作者：Regina Barzilay（MIT,EECS Department, October 1, 2004)
译者：我爱自然语言处理（www.52nlp.cn ，2009年5月5日）

二、 最大熵（Maximum Entropy）：
b) 最大熵模型(Maximum Entropy Modeling)
　iii. 约束条件（Constraint）：
　　每个特征的观察样本期望值与特征模型期望值相一致（observed expectation of each feature has to be the same as the model’s expectation of the feature）：
　　
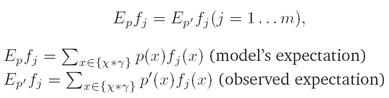
　iv. 最大熵原理(Principle of Maximum Entropy)：
　　将已知事实作为制约条件，求得可使熵最大化的概率分布作为正确的概率分布：
　　　　　
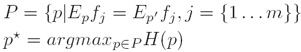
　v. 补充：
　　自然语言处理中很多问题都可以归结为统计分类问题，很多机器学习方法在这里都能找到应用，在自然语言处理中，统计分类表现在要估计类a 和某上下文b 共现的概率P(a,b) ，不同的问题，类a 和上下文b 的内容和含义也不相同。在词性标注中是类的含义是词性标注集中的词类标记，而上下文指的是当前被处理的词前面一个词及词类，后面一个词及词类或前后若干个词和词类。通常上下文有时是词，有时是词类标记，有时是历史决策等等。大规模语料库中通常包含a 和b 的共现信息，但b 在语料库中的出现常常是稀疏的，要对所有可能的(a,b)计算出可靠的P(a,b) ，语料库规模往往总是不够的。问题是要发现一个方法，利用这个方法在数据稀疏的条件下可靠的估计P(a,b) 。不同的方法可能采用不同的估计方法。
　　最大熵模型的优点是：在建模时，试验者只需要集中精力选择特征，而不需要花费精力考虑如何使用这些特征。而且可以很灵活地选择特征，使用各种不同类型的特征，特征容易更换。利用最大熵建模，一般也不需要做在其它方法建模中常常使用的独立性假设，参数平滑可以通过特征选择的方式加以考虑，无需专门使用常规平滑算法单独考虑，当然也不排除使用经典平滑算法进行平滑。每个特征对概率分布的贡献则由参数α决定，该参数可以通过一定的算法迭代训练得到。
（注：以上两段转自北大常宝宝老师的《自然语言处理的最大熵模型》）

三、 最大熵模型详述
a) 概要（Outline）
　i. 我们将首先证明（We will first show that）满足上述条件的概率分布p*具有如下的形式：
　　　　　
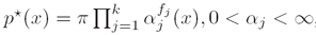
　其中是一个归一化常数，α是模型参数（where  is a normalization constant and the α’s are the model parameters）
　ii. 然后我们将考虑搜寻α的参数估计过程（Then, we will consider an estimation procedure for finding the α’s）
b) 数学符号表示（Notations）
　i. χ是可能的“历史”集（χis the set of possible histories）
　ii. γ是所有可能的标记集（γ is the set of all possible tags）
　iii. S是事件训练样本集（S finite training sample of events）
　iv. p’(x)是S中x的观察概率（p’(x)observed probability of x in S）
　v. p(x)是x的模型概率（p(x) the model’s probability of x）
　vi. 其它符号公式定义如下：
　　　　

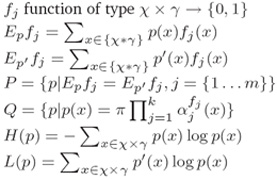
附：课程及课件pdf下载MIT英文网页地址：
　　　http://people.csail.mit.edu/regina/6881/

注：本文遵照麻省理工学院开放式课程创作共享规范翻译发布，转载请注明出处“我爱自然语言处理”：www.52nlp.cn

本文链接地址：http://www.52nlp.cn/mit-nlp-fifth-lesson-maximum-entropy-and-log-linear-models-third-part/