MIT自然语言处理第五讲：最大熵和对数线性模型（第一部分）

自然语言处理：最大熵和对数线性模型
Natural Language Processing: Maximum Entropy and Log-linear Models 
作者：Regina Barzilay（MIT,EECS Department, October 1, 2004)
译者：我爱自然语言处理（www.52nlp.cn ，2009年4月25日）

上一讲主要内容回顾（Last time）：
* 基于转换的标注器（Transformation-based tagger）
* 基于隐马尔科夫模型的标注器（HMM-based tagger）

遗留的内容（Leftovers）: 
a) 词性分布（POS distribution）
　i. 在Brown语料库中按歧义程度排列的词型数目（The number of word types in Brown corpus by degree of ambiguity）：
　　无歧义（Unambiguous）只有1个标记： 35,340
　　　　歧义（Ambiguous） 有2-7个标记： 4,100
　　　　　　　　　　　　　　　　2个标记：3,764
　　　　　　　　　　　　　　　　3个标记：264
　　　　　　　　　　　　　　　　4个标记：61
　　　　　　　　　　　　　　　　5个标记：12
　　　　　　　　　　　　　　　　6个标记：2
　　　　　　　　　　　　　　　　7个标记：1
b) 无监督的TBL（Unsupervised TBL）
　i. 初始化（Initialization）：允许的词性列表（a list of allowable part of speech tags）
　ii. 转换（Transformations）： 在上下文C中将一个单词的标记从χ变为Y (Change the tag of a word from χ to Y in context C, where γ ∈ χ).
　　例子（Example）: “From NN VBP to VBP if previous tag is NNS”
　iii. 评分标准(Scoring criterion):
　　

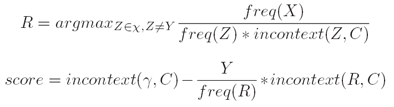
这一讲主要内容（Today）：
* 最大熵模型(Maximum entropy models)
* 与对数线性模型的联系(Connection to log-linear models)
* 优化方法(Optimization methods)

一般问题描述(The General Problem)：
a) 给定输入域χ（We have some input domain χ）；
b) 给定标记集γ（We have some label set γ）；
c) 目标（Goal）：对于任何x ∈ χ 及 y ∈γ学习一个条件概率P(y|x) （learn a conditional probability P(y|x)for any x ∈ χ and y ∈ γ ）。

一、 词性标注（POS tagging）：
a) 例子：Our/PRP$ enemies/NNS are/VBP innovative/JJ and/CC resourceful/JJ ,/, and/CC so/RB are/VB we/PRP ?/?.
　i. 输入域（Input domain）：χ是可能的“历史”（χ is the set of possible histories）；
　ii. 标记集（Label set）：γ是所有可能的标注标记（γ is the set of all possible tags）；
　iii. 目标（Goal）：学习一个条件概率P(tag|history)（learn a conditional probability P(tag|history)）。
b) 表现形式（Representation）：
　i. “历史”是一个4元组(t1,t2,w[1:n],i) （History is a 4-tuples (t1,t2,w[1:n],i)；
　ii. t1,t2是前两个标记（t1,t2 are the previous two tags）
　iii. w[1:n]是输入句子中的n个单词（w[1:n]are the n words in the input sentence）
　iv. i 是将要被标注的单词的位置索引（i is the index of the word being tagged）
　χ是所有可能的“历史”集合（χis the set of all possible histories）

附：课程及课件pdf下载MIT英文网页地址：
　　　http://people.csail.mit.edu/regina/6881/

注：本文遵照麻省理工学院开放式课程创作共享规范翻译发布，转载请注明出处“我爱自然语言处理”：www.52nlp.cn

本文链接地址：http://www.52nlp.cn/mit-nlp-fifth-lesson-maximum-entropy-and-log-linear-models-first-part/