P2260 [清华集训2012]模积和

题目背景

数学题，无背景。

题目描述

求

 

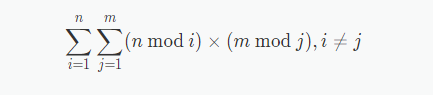
输入输出格式

输入格式：

 

两个整数n m

 

输出格式：

 

答案 mod 19940417

 

输入输出样例

输入样例#1： 复制

3 4

输出样例#1： 复制

1

输入样例#2： 复制

123456 654321

输出样例#2： 复制

116430

说明

30%: n,m <= 1000

60%: n,m <= 10^6

100% n,m <= 10^9

 

 

 

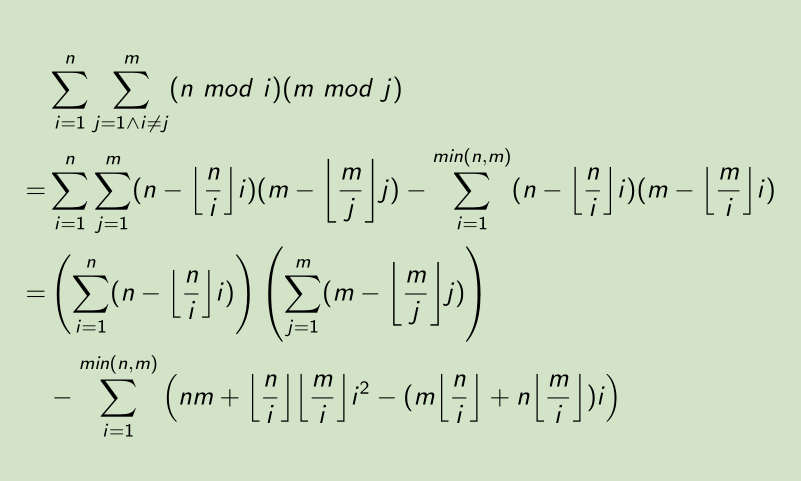
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

const int mod=19940417;

void exgcd(int a,int b,int &x,int &y)
{
    if(!b)
    {
        x=1,y=0;
        return;
    }
    exgcd(b,a%b,y,x);
    y-=a/b*x;
}

int getinv(int num)
{
    int x,y;
    exgcd(num,mod,x,y);
    return (x%mod+mod)%mod;
}

long long n,m;
long long ans;
long long inv6=getinv(6);
long long inv2=getinv(2);

long long sum1(long long a)
{
    return ((a*(a+1)%mod)*(2*a+1)%mod)*inv6%mod;
}

long long sum2(long long l,long long r)
{
    return ((r-l+1)*(l+r)%mod)*inv2%mod;
}

long long calc(long long bound)
{
    long long res=bound*bound%mod;
    for(long long l=1,r;l<=bound;l=r+1)
    {
        if(bound/l)
            r=min(bound,bound/(bound/l));
        else
            r=bound;
        res-=sum2(l,r)*(bound/l);
    }
    return (res+mod)%mod;
}

void work()
{
    ans=calc(n)*calc(m);
    ans%=mod;
    ans-=n*n%mod*m%mod;
    for(long long l=1,r;l<=n;l=r+1)
    {
        if(n/l==0&&m/l==0)
            r=n;
        else
        {
            if(n/l)
                r=min(n,n/(n/l)); 
            if(m/l)
                r=min(r,m/(m/l));
        }
        ans-=(n/l)*(m/l)%mod*(sum1(r)-sum1(l-1))%mod;
        ans+=sum2(l,r)*(m*(n/l)%mod+n*(m/l)%mod)%mod;
        ans%=mod;
    }
    printf("%lld",(ans+mod)%mod);
}

int main()
{
    scanf("%lld%lld",&n,&m);
    if(n>m)
        swap(n,m);
    work();
    return 0;
}