P1457 城堡 The Castle
题目描述
我们憨厚的USACO主人公农夫约翰(Farmer John)以无法想象的运气,在他生日那天收到了一份特别的礼物:一张“幸运爱尔兰”(一种彩票)。结果这张彩票让他获得了这次比赛唯一的奖品——坐落于爱尔兰郊外的一座梦幻般的城堡!
喜欢吹嘘的农夫约翰立刻回到有着吹嘘传统的威斯康辛老家开始吹嘘了, 农夫约翰想要告诉他的奶牛们关于他城堡的一切。他需要做一些吹嘘前的准备工作:比如说知道城堡有多少个房间,每个房间有多大。另外,农夫约翰想要把一面单独的墙(指两个单位间的墙)拆掉以形成一个更大的房间。 你的工作就是帮农夫约翰做以上的准备,算出房间数与房间的大小。
城堡的平面图被划分成M*N(1 <=M,N<=50)个正方形的单位,一个这样的单位可以有0到4面墙环绕。城堡周围一定有外墙环绕以遮风挡雨。(就是说平面图的四周一定是墙。)
请仔细研究下面这个有注解的城堡平面图:
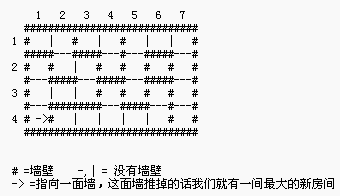
友情提示,这个城堡的平面图是7×4个单位的。一个“房间”的是平面图中一个由“#”、“-”、“|”围成的格子(就是图里面的那一个个的格子)。比如说这个样例就有5个房间。(大小分别为9、7、3、1、8个单位(排名不分先后))
移去箭头所指的那面墙,可以使2个房间合为一个新房间,且比移去其他墙所形成的房间都大。(原文为:Removing the wall marked by the arrow merges a pair of rooms to make the largest possible room that can be made by removing a single wall. )
城堡保证至少有2个房间,而且一定有一面墙可以被移走。
输入输出格式
输入格式:
第一行有两个整数:M和N 城堡的平面图用一个由数字组成的矩阵表示,一个数字表示一个单位,矩阵有N行M列。输入与样例的图一致。
每一个单位的数字告诉我们这个单位的东西南北是否有墙存在。每个数字是由以下四个整数的某个或某几个或一个都没有加起来的。
1: 在西面有墙
2: 在北面有墙
4: 在东面有墙
8: 在南面有墙
城堡内部的墙会被规定两次。比如说(1,1)南面的墙,亦会被标记为(2,1)北面的墙。
输出格式:
输出包含如下4行:
第 1 行: 城堡的房间数目。
第 2 行: 最大的房间的大小
第 3 行: 移除一面墙能得到的最大的房间的大小
第 4 行: 移除哪面墙可以得到面积最大的新房间。
选择最佳的墙来推倒。有多解时选最靠西的,仍然有多解时选最靠南的。同一格子北边的墙比东边的墙更优先。
用该墙的南邻单位的北墙或西邻单位的东墙来表示这面墙,方法是输出邻近单位的行数、列数和墙的方位("N"(北)或者"E"(东))。
输入输出样例
7 4 11 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13
5 9 16 4 1 E
说明
USACO 2.1
翻译来自NOCOW
。。。。luogu拒了我的题解,理由是排版不合理。。。。
/* 个人感觉是一道不错的模拟+搜索的题,做了一上午,做两小时,调一小时,有一些细节需要注意。 ans_sum:房间数量 ans_max:最大的房间的面积 ans_area:把墙推倒后最大的房间的面积 ans_x:推墙的格子的横坐标 ans_y:推墙的格子的纵坐标 ans_dir:推墙的方向 按题目的意思建一个图,每个房间格占一格,墙占一格。 画出来是这个样子: # #O# # 四个角上不用标记为墙,因为拆墙的方向都是平行于x、y轴的。 前两问: ①把图建起来以后跑dfs,把各个房间格连成联通块,变成一个房间。 ②for循环寻找那些没有被连成房间的块,然后从这个点dfs,同时让房间数++。 ③dfs的时候记录当前联通块的面积cnt,以及当前格子属于哪个联通块 ④for循环一遍,dfs的次数就是房间的数量,最大面积ans_max在每次dfs后取max,这样前两问就解决了。 后两问: ①因为题目要求尽量靠西靠南,所以让行i从大到小循环,让列j从小到大循环。 ②将墙推倒能对答案产生贡献的情况当且仅当墙两边的格子不属于同一个房间。 ③如果ans_area小于将当前的墙打穿后两个房间的面积的和,那么直接更新答案。 ④如果ans_area等于将当前的墙打穿后两个房间的面积的和,那么就让ans_y尽量小。 */ #include<iostream> #include<cstdio> #include<cstring> #include<iomanip> #include<algorithm> using namespace std; int n,m,a,cnt,ans_sum,ans_max,ans_area,ans_x,ans_y; char ans_dir; int area[2505]; bool flag[200][200],visited[200][200]; int x_to[4]={0,-2,0,2},y_to[4]={-2,0,2,0}; int xx_to[4]={0,-1,0,1},yy_to[4]={-1,0,1,0}; struct BLO { int area,belong; }blo[200][200]; int read() { char c=getchar();int num=0; for(;!isdigit(c);c=getchar()); for(;isdigit(c);c=getchar()) num=num*10+c-'0'; return num; } void west(int x,int y) //西边有墙 { flag[x][y-1]=0; } void north(int x,int y) //北边有强 { flag[x-1][y]=0; } void east(int x,int y) //东边有墙 { flag[x][y+1]=0; } void south(int x,int y) //南边有墙 { flag[x+1][y]==0; } void work(int a,int x,int y) //当前格子四周墙的位置 { //每个方向的墙设置完后让a减去其对应的值,方便设置其他方向的墙 if(a>=8) //和大于等于8的南边一定有墙 south(x,y),a-=8; if(a>=4) //和大于等于4的东边一定有墙 east(x,y),a-=4; if(a>=2) //和大于2的北边一定有墙 north(x,y),a-=2; if(a==1) //和等于1的西边一定有墙 west(x,y),a-=1; } bool judge(int x,int y) //判断能不能联通 { if(x<1||x>m||y<1||y>n||visited[x][y]) return false; return true; } void dfs(int x,int y) { ++cnt; //当前联通块的面积 blo[x][y].belong=ans_sum; //当前格子属于哪个联通块 visited[x][y]=1; //标记为已联通 for(int i=0;i<4;++i) //向其他四个方向扩展 { int xx=x+x_to[i],yy=y+y_to[i]; if(judge(xx,yy)) if(flag[x+xx_to[i]][y+yy_to[i]]) //要扩展的方向没有墙隔着 dfs(xx,yy); } } int main() { memset(flag,1,sizeof(flag)); n=read(),m=read(); n=n*2-1,m=m*2-1; //矩形的大小,因为房间和墙都占格子,所以*2 for(int i=1;i<=m;++++i) for(int j=1;j<=n;++++j) { a=read(); work(a,i,j); //设置当前格子四周的墙的位置 } for(int i=1;i<=m;++++i) for(int j=1;j<=n;++++j) { if(!visited[i][j]) //不在别的联通块里,找到一个新的房间 { ++ans_sum; //第一问:房间数量++ cnt=0; //房间面积清零 dfs(i,j); area[ans_sum]=cnt; //新的房间的面积 ans_max=max(ans_max,cnt); //第二问:最大房间的面积 } } for(int i=1;i<=m;++++i) //让每一个格子的面积等于它属于的房间的面积 for(int j=1;j<=n;++++j) { blo[i][j].area=area[blo[i][j].belong]; } ans_y=999999999; for(int i=m;i>=1;----i) for(int j=1;j<=n;++++j) { //北面的墙优先 if(blo[i][j].belong!=blo[i-2][j].belong) //要对答案产生贡献,必须两个格子不是同一个房间的 { if(ans_area<blo[i][j].area+blo[i-2][j].area) //能更新推完墙后最大房间的面积ans_area { ans_x=i,ans_y=j,ans_dir='N'; ans_area=blo[i][j].area+blo[i-2][j].area; } else if(ans_area==blo[i][j].area+blo[i-2][j].area) //不能跟新面积,判断是否能更新位置 { if(ans_y>j) //让位置尽量靠西 { ans_x=i,ans_y=j,ans_dir='N'; ans_area=blo[i][j].area+blo[i-2][j].area; } } } if(blo[i][j].belong!=blo[i][j+2].belong) { if(ans_area<blo[i][j].area+blo[i][j+2].area) { ans_area=blo[i][j].area+blo[i][j+2].area; ans_x=i,ans_y=j,ans_dir='E'; } else if(ans_area==blo[i][j].area+blo[i][j+2].area) { if(ans_y>j) { ans_area=blo[i][j].area+blo[i][j+2].area; ans_x=i,ans_y=j,ans_dir='E'; } } } } printf("%d\n",ans_sum); printf("%d\n",ans_max); printf("%d\n",ans_area); printf("%d %d %c\n",(ans_x+1)>>1,(ans_y+1)>>1,ans_dir); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号