【题解】LIS

题意

---

\(n\in\mathbb{N}^*\) ，求长度为 \(n\) 的 \(01\) 序列的最长不下降子序列的长度之和。

思路

---

\(\mathcal O(n^3)\) 做法

直接DP即可

\(\mathcal O(n)\) 做法

其实这不是我的赛时做法，但是有一些奆佬在赛时找规律找出了一个线性做法，因此我想着来证明一下。

如果没有找出的规律，我大概也证明不出这个结论，因为我不会想到这和 \(catlan\) 数有关。

注：以下 \(cat_i\) 均表示卡塔兰数的第 \(i\) 项。

由于已经知道答案和卡塔兰数有关，因此我们考虑把这个01序列表达成一个网格图上的折线。
(注：实际上解法并不依赖于网格图上折线，表达成网格图仅仅为了便于理解，其本身含义只是用坐标表示前缀的 \(1\) 和 \(0\) 的数量，可视化后便于理解）

考虑序列每一项，如果是 \(1\) 就向上一条边，如果是 \(0\) 就向右一条边。
比如序列 \(10010110\)，我们可以把它表示成这样一个折线。
我们要求一个最长不下降子序列，那么我们肯定要找到一个分割点 \((x_0,y_0)\) ，把这个点之前的所有 \(0\) 和这个点之后的 \(1\) 作为最终的最长不下降子序列。
比如在这个序列中，我们会选取分割点 \((2,1)\) 或者 \((3,2)\) ，最终形成的最长不下降子序列分别为 \(1\color{red}{001}0\color{red}{11}0\) 与 \(1\color{red}{00}1\color{red}{011}0\) 。

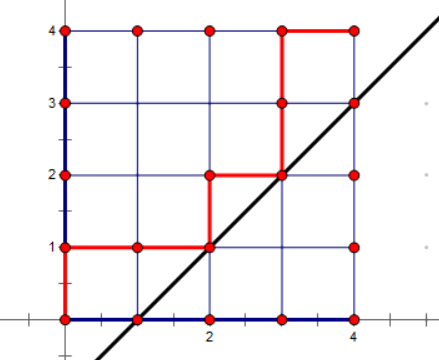
而这个点和 \(LIS\) 的数学上的关系就是：我们假设序列中 \(1\) 有 \(h\) 个，那么最终 \(LIS\) 中 \(0\) 的数量就是 \(x_0\) ， \(1\) 的数量就是 \(h-y_0\) ,也就是 \(LIS\) 的长度为 \(h+x_0-y_0\) 。
设 \(x_0-y_0=k\) ，那么就有 \(y=x-k\) 。我们希望 \(k\) 最大，同时显然有这条线与折线有交点，因此我们可以很容易画出 \(k\) 取到的最大的时候的 \(y=x-k\)。（即图中黑线）

现在我们考虑来递推答案。记答案为 \(f_n\) 那么当一个长度为 \(n\) 的序列后面加上一个 \(1\) 那么无论如何 \(LIS\) 都会增加 \(1\) ，这一部分对 \(f_{n+1}\) 的贡献为 \(f_n+2^n\)。

下面考虑序列后加 \(0\) 的情况。

我们会发现 \(h\) 是不变的，我们只需要考虑这条黑线是否变化即可。
显然黑线变化当且仅当长度为 \(n\) 的序列所代表折线中最后一个点在黑线上。

我们记这样的线有 \(g_n\) 条，而这依然需要递推。

考虑在长度为 \(n\) 的序列前加一个 \(1\) 或者 \(0\) ，如果加 \(0\) ，那么原来最后一点在黑线上，现在依然在黑线上，这一部分的贡献是 \(g_n\)。
而如果加 \(1\) ，那么只有黑线变化的时候是不对 \(g_{n+1}\) 做贡献的，而黑线变化当且仅当原来的起始点也在黑线上。（如图）
此时如果从起始点向下画一条线，那么黑线的位置会发现变化。

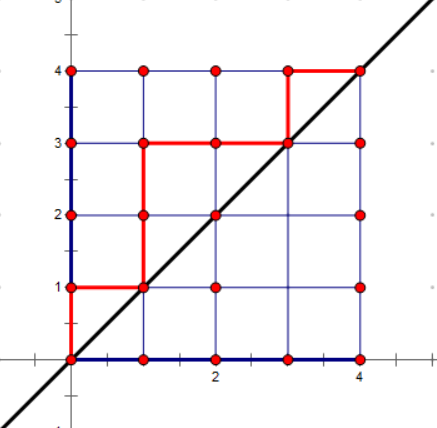
从而这样的黑线一定经过 \((0,0)\)，因此最后黑线必然为 \(y=x\) ，且折线一定在 \(y=x\) 上方，折线终点也必然在 \(\left(\dfrac{n}{2},\dfrac{n}{2}\right)\) ，这显然是卡塔兰数的经典套路，需要 \(n\) 为偶数，且总数为 \(cat_{\frac{n}{2}}\)。

从而我们有 \(g_n\) 的递推式为：\(g_{2n}=2g_{2n-1},g_{2n+1}=2g_{2n}-cat_n\)
\(f_n\) 的递推式则为: \(f_{n+1}=(f_n+2^n)+(f_n+g_n)=2f_n+2^n+g_n\)
卡塔兰数和组合数都可以通过预处理阶乘、逆元以及阶乘逆元计算，\(f_n\) 和 \(g_n\) 的递推都是 \(\mathcal O(n)\) 的，因此最后复杂度为 \(\mathcal O(n)\)。