博弈-三个枪手决斗

三人决斗问题（枪手博弈）

题目是这样的：

A、B、C三人进行决斗。A 的射击命中率是三分之一，也就是说如果他努力的话，他平均每三枪可以击中一次；B 的射击命中率是二分之一；C 的射击命中率是一（也就是百分之百）。由于 A 的命中率最低，为公平起见，他们让 A 先射，然后是 B（如果他还活着的话），然后是 C（如果他还活着的话）。再然后是 A，B，C，如此循环下去，直到只有一人活着。每次射击时只能开一枪，但可以选择朝哪里开，也可以选择放空枪。我们的问题是：如果ABC三人都按照最佳选择行事，也就是说尽可能的提高自己地存活率，谁活下来的可能性最大？准确一点，每个人活下来的概率是多少？

根据题意，在第一轮射击过程中，我们可以有三个比较明显的推断：

1) 由于 C 的命中率为100%，A、B 第一轮如果互相攻击则无异于找死；
2) C 在 A 与 B 中，会优先射 B，因为 B 的命中率 1/2 大于 A 的命中率 1/3，不可养虎为患；
3) B 会射 C，B 先于 C 开枪，若其推断出 C 会优先射击自己，则一定会先射 C，因为投降则必死，不如一博。

接下来，我们可以先把问题简化一下，先考虑只有两个人的情形。注意到 C 的命中率有100%，因此无论只有 A 与 C 还是只有 B 与 C，情况都比较简单，如果轮到 C 开枪则 C 获胜。

比如，如果现在只有 A 与 C 决斗，则如果 A 先开枪，A 的存活率为 1/3 （他一枪命中的情况），如果 C 先开枪，则 A 必死。

现在考虑如果只有 A 和 B 决斗，情况会怎么样，显然，在只有两个人的情况下，如果双方都想尽可能地提高自己的存活率，则不会有人放空枪。假设此时轮到 A 开枪，则：

1) A 开枪，有 1/3 的机会击中 B 获胜，2/3 的机会未击中，进入下一轮；
2) B 开枪，有 1/2 的机会击中 A 获胜，1/2 的机会未击中，进入下一轮；
3) 重复以上步骤，直到有一人获胜。

如下图所示：

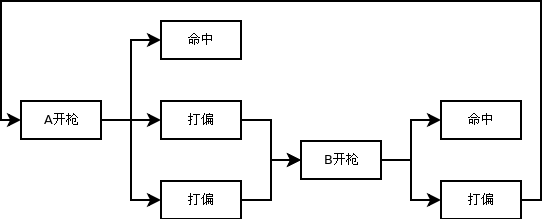
当只有 A、B 决斗时，如 A 先开枪，则 A、B 的存活概率 P(A1)、P(B1) 分别为：

P(A1)
= 1/3 + 1/3 * (1/3 + 1/3 * …)
= 1/3 * (1 + 1/3 + (1/3) ^ 2 + …)
= 1/3 * (1/(1 – 1/3))
= 1/2

对应地有 P(B1) = 1 – P(A1) = 1 – 1/2 = 1/2 。

如 B 先开枪，则 A、B 的存活概率 P(A2)、P(B2) 分别为：

P(A2) = P(A1) * 1/2 = 1/4 （相当于 B 先开一次枪后再进行上面 A 先开枪的步骤。）

对应地有 P(B2) = 1 – P(A2) = 1 – 1/4 = 3/4 。

显然，在 B 与 C 之间，A 更不希望与 C 决斗。上面的 P(A1)、P(B2) 下面还会用到。

如果 A 第一枪射 B ，则他有 1/3 的概率直接射中 B，然后被 C 打死，2/3 的概率进入下一轮决斗，即 A 有 1/3 的概率在第一轮就挂掉。下一轮中他有 1/2 的概率与 B 决斗，1/2 的概率与 C 决斗，情况看起来不是很妙。

如果 A 与 B 同仇敌忾，第一枪先一起射 C 呢？他将有 1/3 的概率射中 C，然后被 B 以 1/2 的概率射中，即如果他先射 C，则有 1/3 * 1/2 = 1/6 的概率在第一轮就挂掉。

那如果 A 第一轮放空枪呢？这时，B 显然会射 C，如果射中（1/2 概率），则进入 A、B 决斗的情况，并且是 A 先开枪，A 有 1/2 的概率存活；如 B 未射中 C（1/2 概率），则轮到 C 开枪时 C 显然会把 B 干掉，进入 A、C 决斗的情况，A 先开枪，此时 A 有 1/3 的存活概率。

显然，A 第一轮放空枪是一种更好的策略。此时，A、B、C 三人决斗可能的流程如下图所示：

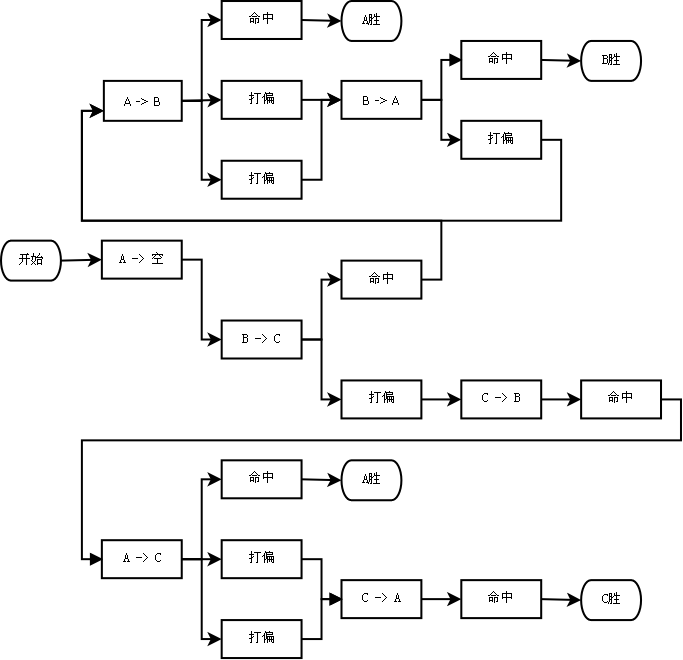
其中 A、B、C 三人存活的概率分别为：

P(A) = 1/2 * 1/3 + 1/2 * P(A1) = 1/6 + 1/3= 5/12

P(B) = 1/2 * P(B2) = 1/4

P(C)=(1 – 1/2) * (1 – 1/3) = 1/3

其中 P(A1)、P(B2) 即是上面只有 A、B 两人决斗时计算得到的中间变量。

可以看到，P(A) > P(C) > P(B)，A 的存活概率最大（接近于 1/2），C 的存活概率次之，B 的存活概率最小。

分析方法值得学习，由简入深，依次递推。