逻辑回归

二分类问题：

线性回归，就是根据数据，学习出事情的规律，而如果设定一些条件，将其划到一种类别中去，也就是通过线性回归加设定阈值的办法，就可以完成一个简单的二分类任务。

逻辑回归：

利用线性回归的办法来拟合，然后设置阈值的办法容易受到离群值的影响，因此sigmoid函数可以有效的帮助我们解决这一个问题。即把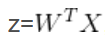变成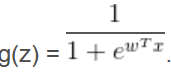

逻辑回归表达式：

逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0到1之间。线性回归模型的表达式带入g(z)，就得到逻辑回归的表达式:

 

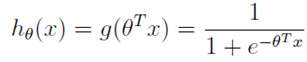
 由于g(z)函数本身的性质，它输出的结果是预测为正的概率，则为负的概率为1-g(z)。

构建极大似然函数(取对后)：

 

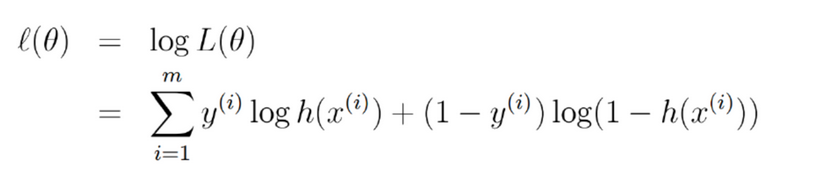
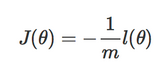
J(θ)也称之为代价函数：衡量的是模型的错误程度

梯度下降

梯度下降是通过 J(θ) 对θ 的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为：

 

 

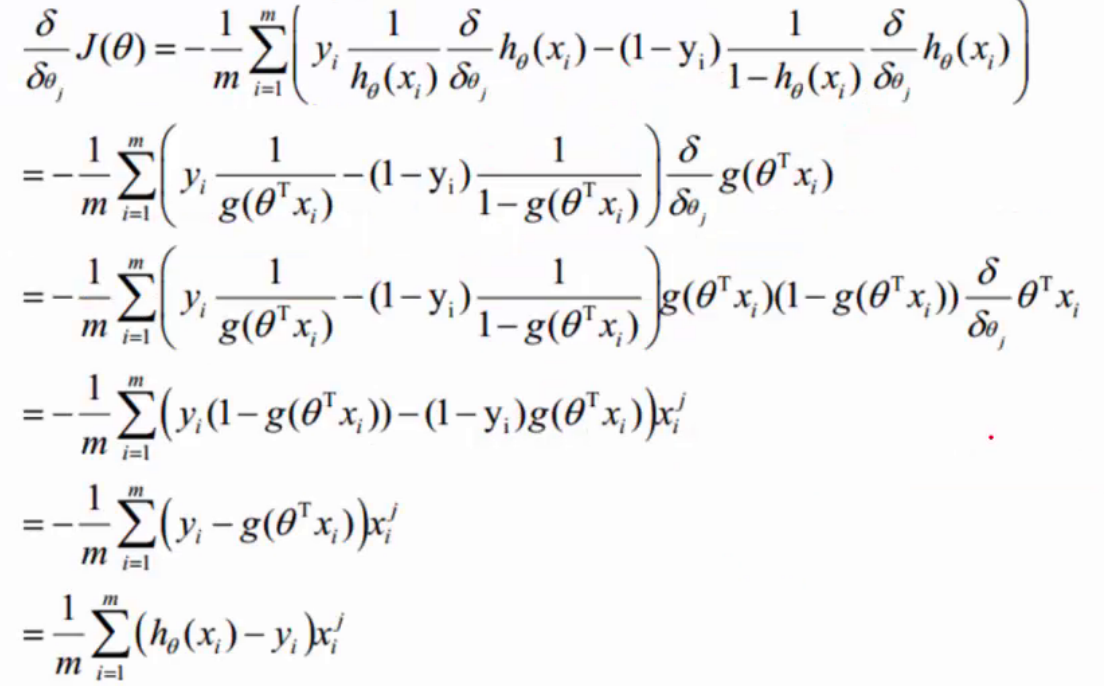
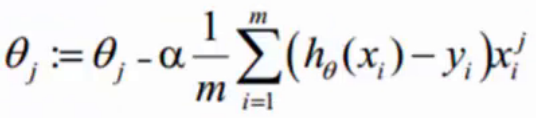
最后使得分类结果更加趋近于0，1两端，从而达到分类效果

正则化：L1 正则化(LASSO回归)、L2 正则化(Ridge回归)

防止过度拟合，用来修正参数值。

L1 和 L2 的区别：L1 正则化增加了所有权重 w 参数的绝对值之和逼迫更多 w 为零，也就是变稀疏，它会学习地去掉这些无用的特征，也就是把这些特征对应的权重置为 0。L2 正则化中增加所有权重 w 参数的平方之和，逼迫所有 w 尽可能趋向零但不为零，即惩罚权重。

参考：

https://www.cnblogs.com/God-Li/p/8999023.html