红黑树以及和AVL的比较

红黑树介绍：

红黑树是解决二叉查找树(左孩子的结点值<该结点值<右孩子结点值)不平衡的解决方案，即是为了平衡二叉查找树。

红黑树每个结点遵循一下规则：

1. 每个结点都有红色或者黑色

2. 树根始终是黑色的

3. 没有两个相邻的结点都是红色的

4. 从结点(包括根)开始到其后代的NULL结点(叶子结点下面有两个空结点，他们是黑色的)的每条路径都有相同数量的黑色结点。

步骤：

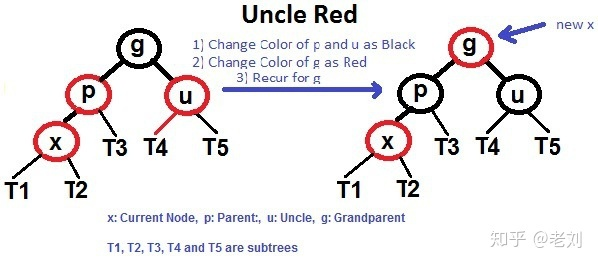
若X的uncle是红色：

1. 将新插入的 X 节点标记为红色
2. 发现 X 的 parent (P) 同样为红色，这违反了红黑树的第三条规则「不能有两个连续相邻的红色节点」
3. 发现 X 的 uncle (U) 同样为红色
4. 将 P 和 U 标记为黑色
5. 将 X 和 X 的 grand parent (G) 标记为相同的颜色，即红色，继续重复公式 2、3
6. 发现 G 是根结点，标记为黑色
7. 结束

 

 

若X的uncle是黑色：

1.若X的parent是红色，同时X不是root

左左情况：

 

 

 

左右

 

 

 

右右

 

 

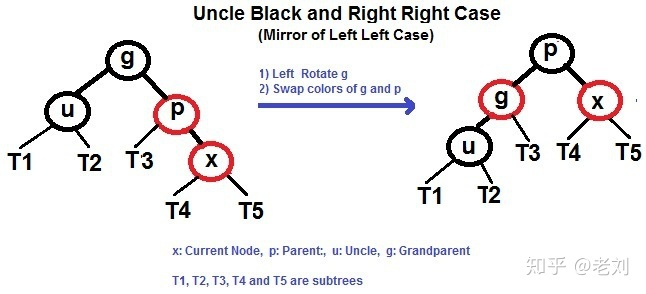
右左

 

 

红黑树和AVL比较：

红黑树不追求“完全平衡 ”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。AVL(平衡二叉树)是严格的平衡，它要求它的左子树和右子树都是AVL且左右子树高度差不能超过1。

他们搜索、插入、删除的时间复杂度都是O(logn)，但是AVL增加和删除操作可能需要多次旋转来平衡树，而对于红黑树，任何不平衡都会在三次旋转内得到解决。

总体来说红黑树算法时间复杂度和AVL相等，但其统计性能比AVL好。

 

参考：

https://zhuanlan.zhihu.com/p/79980618