排序问题之归并排序

排序问题

算法问题的基础问题之一，便是排序问题：

　　输入：n个数的一个序列，<a₁, a₂,..., a_n>。

　　输出：一个排列<a_1^',a_2^', ... , a_n'>，满足a_1^' ≤ a_2^' ≤... ≤ a_n' 。（输出亦可为降序，左边给出的例子为升序）

一.算法描述

    （1）分治法

      归并排序是使用到了分治方法（Divide and Conquer）。

　　Divide：将原问题分解为若干子问题，其中这些子问题的规模小于原问题的规模。

　　Conquer：递归地求解子问题，当子问题规模足够小时直接求解。

　　Merge：将子问题的解合并得到原问题的解。

　（2）归并排序的分治思想

      分解：分解待排序的n个元素序列为各具n/2个元素的子序列

　　解决：使用归并排序递归地对子序列排序

　　合并：合并两个已排序的子序列

   （3）归并排序

      MergeSort：假设我们要对一个输入规模为n的序列A[1,2, ... , n]进行排序，我们可以考虑将该序列一分为二，左边为A_left[1, 2, ... , ⌈n/2⌉]，右边为A_right[⌈n/2⌉+1, ... , n]。然后分别对两边规模为n/2的子问题进行求解，并将两个解合并。（⌈n/2⌉是n除以2的向上取整结果）

　　Merge：合并算法是将两个有序的序列A和B合并为一个有序的序列，这个过程只需要我们每次都取出A和B队列的对首加入一个新队列的末尾即可，直至某一个队列为空，将另一个队列的剩余元素补到新队列后面。

     

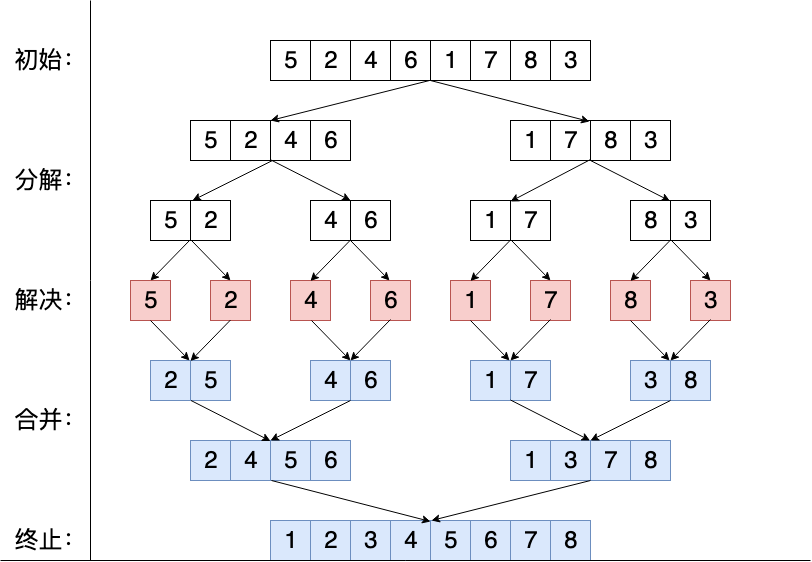
     下面我们给出一个对序列[5, 2, 4, 6, 1, 3, 8, 7]使用归并排序得到递增序列的过程。在图中白色的部分是未排序的序列，每一层将序列规模折半分成左右两个子序列排序，直至问题规模将为1，子问题规模足够小时可以直接求解，而规模为1的序列本身就是有序的，所有不需要进行任何操作。最后一步是将所有子问题的解合并，每次都将两个有序序列合并为一个有序序列，直至只剩下一个有序序列时终止。

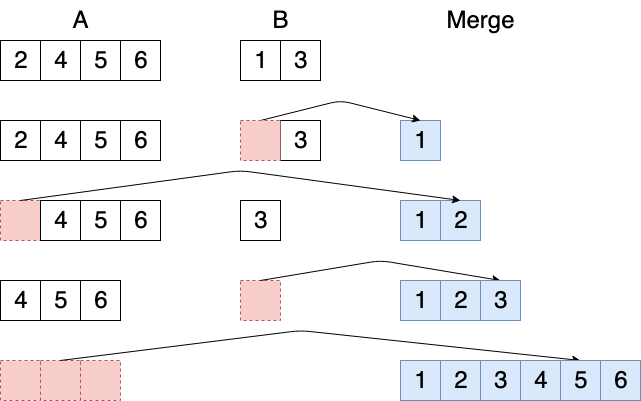
      下图则给出了一个合并算法的例子。对于A,B两个排序好的序列，每次取出A、B之中的较小值放入归并后的序列，直到B中元素被取完，直接将A中的剩余元素按顺序尾插到Merge序列中，就能得到A与B的合并。

二.代码实现

      下面是归并排序的C++实现：

#include<iostream>
#include<cmath>
using namespace std;
/**
 * @brief 对两个有序序列合并
 * @param arr    原数组
 * @param start  待合并的数组起始下标
 * @param end    待合并的数组结尾下标
 * @param result 合并后的数组
 */
void Merge(int* arr, int start, int end, int* result){
    
    int i,j = 0;
    int mid = (ceil(start + end)/2);
    int left_index = start;
    int right_index = mid + 1;
    int result_index = start;

    //左右都非空时，循环取左右中的最小元素尾插到result数组
    while( left_index < mid + 1 && right_index < end + 1){
        if(arr[left_index] <= arr[right_index]){
            result[result_index] = arr[left_index];
            left_index++;
        }
        else{
            result[result_index] = arr[right_index];
            right_index++;
        }
        result_index++;
    }

    //左右有一个为空，则将非空的数组元素放到result末尾
    while(left_index < mid + 1){
        result[result_index] = arr[left_index];
        result_index++;
        left_index++;
    }
    while(right_index < end + 1){
        result[result_index] = arr[right_index];
        result_index++;
        right_index++;
    }
}

/**
 * @brief 归并排序
 * @param arr    待排序的数组
 * @param start  待排序的数组起始下标
 * @param end    待排序的数组结尾下标
 * @param result 保存临时结果的数组
 */
void MergeSort(int* arr, int start, int end, int* result)
{
    //规模为0时不需进行任何操作
    if(0 == end - start){
        return;
    }
    else{

        //递归地对左右序列排序，合并到result中以后覆盖arr中的对应位置元素
        MergeSort(arr,start,ceil((start+end)/2), result);
        MergeSort(arr,ceil((start+end)/2)+1,end, result);
        Merge(arr,start,end,result);
        for(int i = start; i <= end; i++){
            arr[i] = result[i];
        }

    }

}
    


int main()
{
    int arr[10] = {5,2,4,7,10,9,8,1,6,3};
    int result[10];
    MergeSort(arr,0,9,result);

    for(int i = 0; i < 10; i++){
        cout << arr[i] <<' ';
    }
    
}

 

 

三.算法分析

（1）时间复杂度

　　 对于最好，最坏和平均情况，问题都要将规模分解到1为止，所以三者的时间复杂度相同。

　　 T(n) = 2T(n/2) + θ(n)　　n > 1时

　　 T(n) = θ(1)　　　　　　   n = 1时

　　 通过画递归树分析可知T(n) = cnlgn + cn, 时间复杂度即为θ(nlgn)，当然也为o(nlgn)。

（2）稳定性

　　 稳定性是指对于原有序列中的等值元素，是否在排序后不改变它们的相对顺序关系。归并时当左边不大于右边时先取左边的元素，遵循这样的规律时归并排序就是稳定的。

（3）适合范围

       一般用于对总体无序，但是各子项相对有序的数列。

（4）算法改进

　　 TimSort，结合了插入排序来优化，具体不详细展开。