二叉堆 与 PriorityQueue
欢迎光临我的博客[http://poetize.cn],前端使用Vue2,聊天室使用Vue3,后台使用Spring Boot
堆在存储器中的表示是数组,堆只是一个概念上的表示。堆的同一节点的左右子节点都没有规律。
堆适合优先级队列(默认排列顺序是升序排列,快速插入与删除最大/最小值)。
数组与堆
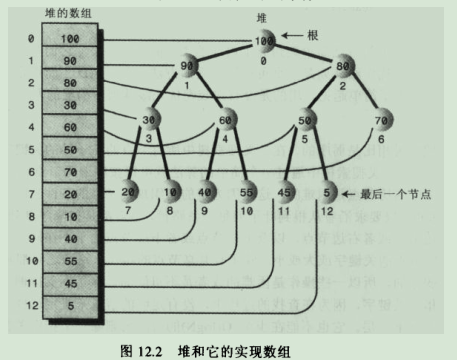
堆(完全二叉树)(构造大顶堆或者小顶堆的时间复杂度:O(logn))
堆实现的优先级队列虽然和数组实现相比删除慢了些,但插入的时间快的多了:
当速度很重要且有很多插入操作时,可以选择堆来实现优先级队列。
堆插入删除的效率:时间复杂度是:O(logn)。
小顶堆:父节点的值 <= 左右孩子节点的值
大顶堆:父节点的值 >= 左右孩子节点的值
堆的定义:n个关键字序列array[0,...,n-1]:
若array[0,...,n-1]表示一颗完全二叉树的顺序存储模式,则双亲节点指针和孩子结点指针之间的内在关系如下:
任意一节点指针 i(0 <= i <= (n-1)/2) : 父节点:i==0 ? null : (i-1)/2
左孩子:2*i + 1
右孩子:2*i + 2
① array[i] <= array[2*i + 1] 且 array[i] <= array[2*i + 2] : 称为小根堆
② array[i] >= array[2*i + 1] 且 array[i] >= array[2*i + 2] : 称为大根堆
堆的插入( add(e),offer(e) ):添加到末尾,由于可能破坏堆结构,需要调整(向上筛选)
插入使用向上筛选,向上筛选的算法比向下筛选的算法相对简单,因为它不需要比较两个子节点关键字值的大小
删除操作 ( remove(o) ):由于可能破坏堆结构,需要调整(向下筛选)
删除堆顶 ( poll() ):由于可能破坏堆结构,需要调整(向下筛选)
移除是指删掉关键字值最大的节点,即根节点。
在被筛选节点的每个暂时停留的位置,向下筛选的算法总是要检查哪一个子节点更大,然后目标节点和较大的子节点交换位置
堆排序(时间复杂度:O(nlogn))
堆排序是一种树形选择排序方法,它的特点是:
在排序的过程中,将array[0,...,n-1]看成是一颗完全二叉树的顺序存储结构,
利用完全二叉树中双亲节点和孩子结点之间的内在关系,在当前无序区中选择关键字最大(最小)的元素。
步骤:
构造堆
固定最大值再构造堆(将最大值元素(堆头)与堆尾元素交换,将其他数再构造成最大堆)
重复上述过程
堆(二叉堆)排序的时间复杂度,最好,最差,平均都是O(nlogn),空间复杂度O(1),是不稳定的排序。
PriorityQueue
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
private static final long serialVersionUID = -7720805057305804111L;
private static final int DEFAULT_INITIAL_CAPACITY = 11;
transient Object[] queue; // non-private to simplify nested class access
int size;
private final Comparator<? super E> comparator;
transient int modCount; // non-private to simplify nested class access
public PriorityQueue(Collection<? extends E> c) {} //使用已有集合构建二叉堆
public PriorityQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
public PriorityQueue(int initialCapacity,
Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.queue = new Object[initialCapacity];
this.comparator = comparator;
}
}
//自定义比较器,降序排列
static Comparator<Integer> cmp = new Comparator<Integer>() {
public int compare(Integer e1, Integer e2) {
return e2 - e1;
}
};
在未排序的数组中找到第 k 个最大的元素
/**
* 示例 1:
* 输入: [3,2,1,5,5,4] 和 k = 2
* 输出: 5
*
* 时间复杂度 : O(Nlogk)。
* 空间复杂度 : O(k),用于存储堆元素。
*/
/**
* 小顶堆
*/
class Solution {
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 0; i < nums.length; i++) {
pq.add(nums[i]);
if(pq.size()>k)pq.poll();
}
return pq.poll();
}
}
找出动态有序列表的中位数
/**
* 中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
*
* 例如,
* [2,3,4] 的中位数是 3
* [2,3] 的中位数是 (2 + 3) / 2 = 2.5
*
* 方法:最大堆与最小堆。
* 思路:各存储一半,最大堆的堆顶比最小堆的堆顶小。
*
* 时间复杂度:O(logN),从堆里得到一个 “最值” 而其它元素无需排序
* 空间复杂度:O(N)
*/
class MedianFinder1 {
/**
* 当前大顶堆和小顶堆的元素个数之和
*/
private int count;
private PriorityQueue<Integer> maxheap;
private PriorityQueue<Integer> minheap;
/**
* initialize your data structure here.
*/
public MedianFinder1() {
count = 0;
maxheap = new PriorityQueue<>((x, y) -> y - x); //大顶堆
minheap = new PriorityQueue<>(); //小顶堆
}
public void addNum(int num) {
count += 1;
maxheap.offer(num);
minheap.add(maxheap.poll());
// 如果两个堆合起来的元素个数是奇数,小顶堆要拿出堆顶元素给大顶堆
if ((count & 1) != 0) {
maxheap.add(minheap.poll());
}
}
public double findMedian() {
if ((count & 1) == 0) {
// 如果两个堆合起来的元素个数是偶数,数据流的中位数就是各自堆顶元素的平均值
return (double) (maxheap.peek() + minheap.peek()) / 2;
} else {
// 如果两个堆合起来的元素个数是奇数,数据流的中位数大顶堆的堆顶元素
return (double) maxheap.peek();
}
}
}

