欢迎光临我的博客[http://poetize.cn],前端使用VUE2,聊天室使用VUE3,后台使用Spring Boot
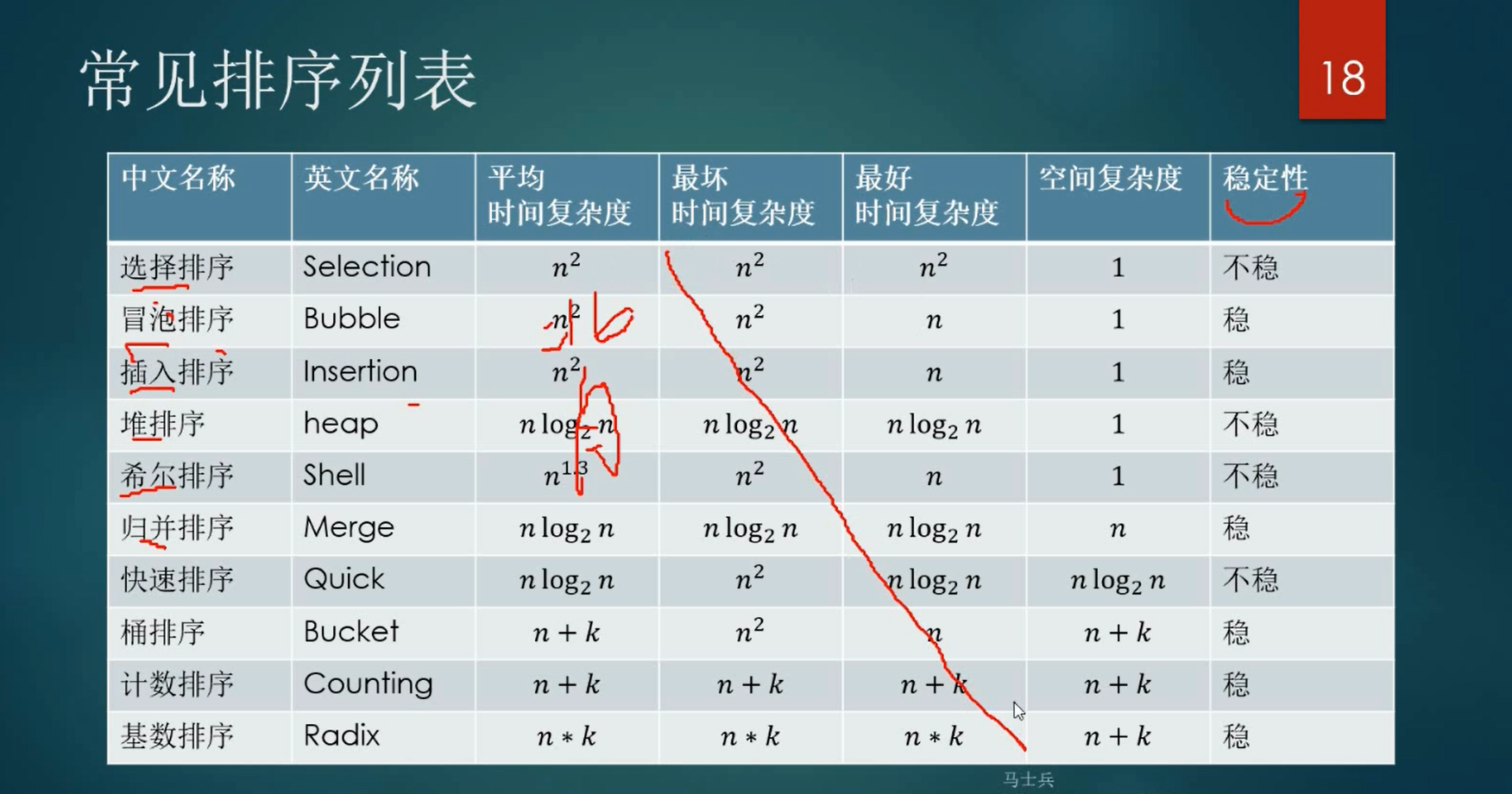
直接插入排序基本思想
插入排序对于少量元素的排序是很高效的
把n个待排序的元素看成为一个有序表和一个无序表。
开始时有序表中只包含1个元素,无序表中包含有n-1个元素,
排序过程中每次从无序表中取出第一个元素,将它插入到有序表中的适当位置,使之成为新的有序表,
重复n-1次可完成排序过程。

直接插入排序复杂度
最好情况:序列是升序排列,在这种情况下,需要进行的比较操作需(n-1)次。后移赋值操作为0次。
即O(n)
时间复杂度:o(n^2)
直接插入排序是稳定的,不会改变相同元素的相对顺序。
1 class InsertionSort {
2
3 public void sort() {
4 int[] arr = {1, 32, 1, 2, 43, 5,};
5
6 if (arr == null || arr.length < 2) {
7 return;
8 }
9
10 for (int i = 1; i < arr.length; i++) {
11 //无序的第一个
12 int temp = arr[i];
13 //有序的最后一个
14 int j = i - 1;
15 //当未达到数组的第一个元素或者待插入元素小于当前元素
16 while (j >= 0 && arr[j] > temp) {
17 //就将该元素后移
18 arr[j + 1] = arr[j];
19 j--;
20 }
21 if (j + 1 != i) {
22 arr[j + 1] = temp;
23 }
24 }
25 }
26 }
二分插入排序
在有序区中查找新元素插入位置时,为了减少元素比较次数提高效率,
采用二分查找算法进行插入位置的确定。
二分查找最坏时间复杂度:O(log2n)
所以,二分查找排序比较次数为:x=log2n
二分查找插入排序耗时的操作有:比较 + 后移赋值。时间复杂度如下:
1) 最好情况:查找的位置是有序区的最后一位后面一位,则无须进行后移赋值操作,
其比较次数为:log2n。即O(log2n)
2) 最坏情况:查找的位置是有序区的第一个位置,则需要的比较次数为:log2n,
需要的赋值操作次数为n(n-1)/2加上 (n-1) 次。即O(n^2)
3) 渐进时间复杂度(平均时间复杂度):O(n^2)
二分查找排序是稳定的,不会改变相同元素的相对顺序。




