对旋转矩阵R做（行）初等变换会发生什么？

　前言：最近在做一个有意思的问题，关于旋转矩阵变换后会发生什么？开始猜想对其做行初等变换，应该不会改变旋转矩阵的实质的旋转性质。但测试结果好像跟猜想不太一样？

　测试：

　　1、第一次对旋转矩阵R的某一行乘上一个数，然后将R转换为欧拉角和四元数；

　　2、第二次对旋转矩阵R的某一行乘上一个数加到另一行上，然后将R转换为欧拉角和四元数；

 

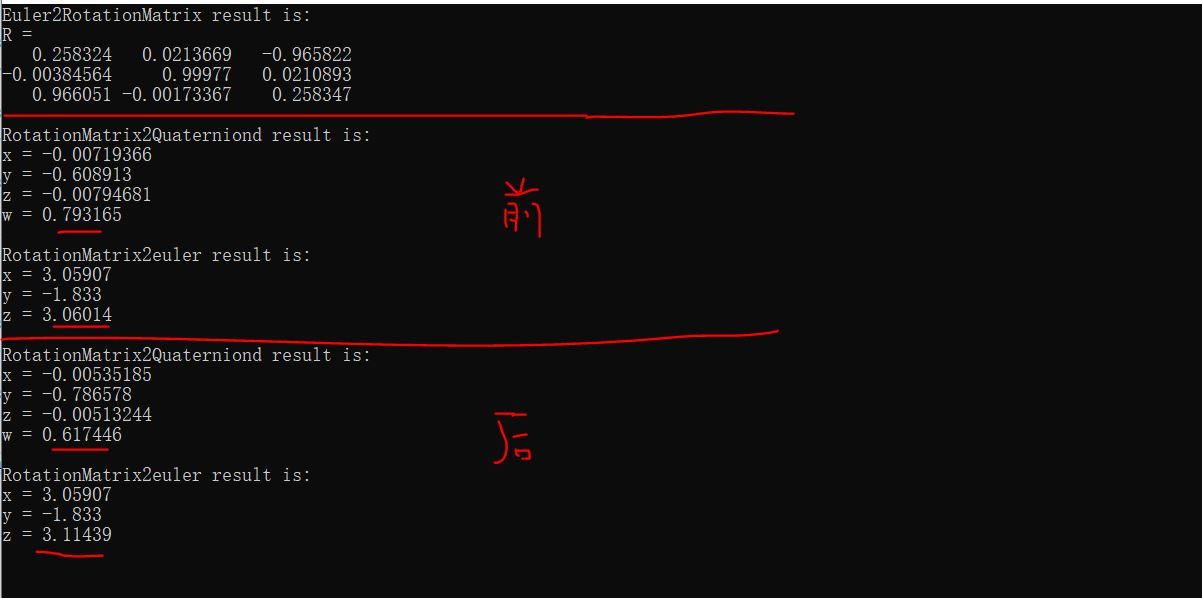
图1 测试1

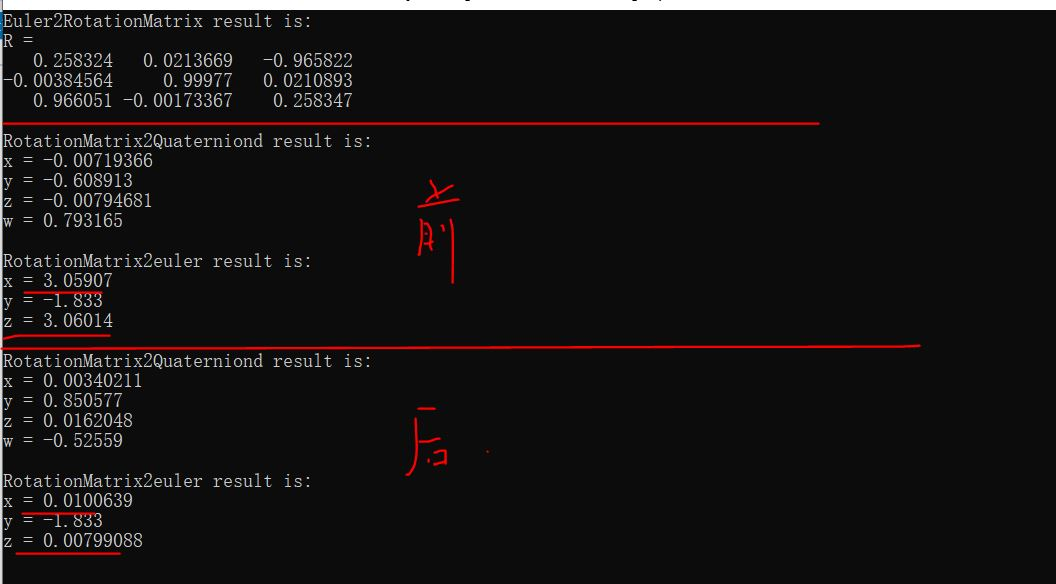
 图2 测试2

代码：

#include <iostream>
#include <stdlib.h>
#include <Eigen/Eigen>
#include <Eigen/Geometry>
#include <Eigen/Core>
#include <vector>
#include <math.h>
using namespace std;
using namespace Eigen;

Eigen::Quaterniond euler2Quaternion(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    q.normalize();
    cout << "Euler2Quaternion result is:" << endl;
    cout << "x = " << q.x() << endl;
    cout << "y = " << q.y() << endl;
    cout << "z = " << q.z() << endl;
    cout << "w = " << q.w() << endl << endl;
    return q;
}

Eigen::Vector3d Quaterniond2Euler(const double x, const double y, const double z, const double w)
{
    Eigen::Quaterniond q;
    q.x() = x;
    q.y() = y;
    q.z() = z;
    q.w() = w;
    Eigen::Vector3d euler = q.toRotationMatrix().eulerAngles(2, 1, 0);
    cout << "Quaterniond2Euler result is:" << endl;
    cout << "x = " << euler[2] << endl;
    cout << "y = " << euler[1] << endl;
    cout << "z = " << euler[0] << endl << endl;

    return euler;
}

Eigen::Matrix3d Quaternion2RotationMatrix(const double x, const double y, const double z, const double w)
{
    Eigen::Quaterniond q;
    q.x() = x;
    q.y() = y;
    q.z() = z;
    q.w() = w;
    Eigen::Matrix3d R = q.normalized().toRotationMatrix();
    cout << "Quaternion2RotationMatrix result is:" << endl;
    cout << "R = " << endl << R << endl << endl;
    return R;
}
Eigen::Quaterniond rotationMatrix2Quaterniond(Eigen::Matrix3d R)
{
    Eigen::Quaterniond q = Eigen::Quaterniond(R);
    q.normalize();
    cout << "RotationMatrix2Quaterniond result is:" << endl;
    cout << "x = " << q.x() << endl;
    cout << "y = " << q.y() << endl;
    cout << "z = " << q.z() << endl;
    cout << "w = " << q.w() << endl << endl;
    return q;
}

Eigen::Matrix3d euler2RotationMatrix(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    Eigen::Matrix3d R = q.matrix();
    cout << "Euler2RotationMatrix result is:" << endl;
    cout << "R = " << endl << R << endl << endl;
    return R;
}
Eigen::Vector3d RotationMatrix2euler(Eigen::Matrix3d R)
{
    Eigen::Matrix3d m;
    m = R;
    Eigen::Vector3d euler = m.eulerAngles(0, 1, 2);
    cout << "RotationMatrix2euler result is:" << endl;
    cout << "x = " << euler[2] << endl;
    cout << "y = " << euler[1] << endl;
    cout << "z = " << euler[0] << endl << endl;
    return euler;
}

Eigen::Matrix3d matrixTransion(Eigen::Matrix3d& R)
{
    Eigen::Matrix3d M(R);

    //M(0, 2) = R(0, 1) * (-1) * 3 + R(0, 2);
    //M(1, 2) = R(1, 1) * (-1) * 3 + R(1, 2);
    //M(2, 2) = R(2, 1) * (-1) * 3 + R(2, 2);

    M(2, 0) = R(0, 0)*3 + R(2, 0);
    M(2, 1) = R(0, 1)*3 + R(2, 1);
    M(2, 2) = R(0, 2)*3 + R(2, 2);

    return M;
}



int main(int argc, char **argv)
{
    //this is euler2Quaternion transform function,please input your euler angle//
    //euler2Quaternion(2.55356, - 0.751701, -35.1082);    //-0.0148858, -0.00671055, -1.30948
    //Eigen::Quaterniond q = Eigen::Quaterniond(-0.00482526, 0.00153114, 0.997521, -0.0701826);
    //q.normalize();
    //cout << " test q:: "<< endl;
    //cout << "x = " << q.x() << endl;
    //cout << "y = " << q.y() << endl;
    //cout << "z = " << q.z() << endl;
    //cout << "w = " << q.w() << endl << endl;
    //"w":1.23782,"x":-0.013243,"y":-0.00426015,"z":-0.390197

    //this is Quaternion2Euler transform function,please input your euler angle//
    //Quaterniond2Euler(0, 0, 0, 1);

    //this is Quaternion2RotationMatrix transform function,please input your Quaternion parameter//
    //Quaternion2RotationMatrix(0, 0, 0, 1);

    //this is euler2RotationMatrix transform function,please input your euler angle for the function parameter//
    Eigen::Matrix3d R = euler2RotationMatrix(-0.0148858, -0.00671055, -1.30948);
    rotationMatrix2Quaterniond(R);
    RotationMatrix2euler(R);

    Eigen::Matrix3d M = matrixTransion(R);
    //this is rotationMatrix2Quaterniond transform function,please input your RotationMatrix parameter like following//
    rotationMatrix2Quaterniond(M);

    //this is RotationMatrix2euler transform function,please input your euler angle for the function parameter//
    RotationMatrix2euler(M);

    return 0;
}

 

　　结论：变换前后欧拉角和四元数变化了，这说明旋转矩阵R 是不能做初等变换的，而且齐次变换矩阵T（RT）也是不能做初等变换的。