稀疏线程方程求解

二、稀疏矩阵分解

 

稀疏矩阵类

 

#include <Eigen/Sparse>
#include <vector>
#include <iostream>
typedef Eigen::SparseMatrix<double> SpMat; // declares a column-major sparse matrix type of double
typedef Eigen::Triplet<double> T;
void buildProblem(std::vector<T>& coefficients, Eigen::VectorXd& b, int n);
void saveAsBitmap(const Eigen::VectorXd& x, int n, const char* filename);
int main(int argc, char** argv)
{
if(argc!=2) {
std::cerr << "Error: expected one and only one argument.\n";
return -1;
}
int n = 300; // size of the image
int m = n*n; // number of unknows (=number of pixels)
// Assembly:
std::vector<T> coefficients; // list of non-zeros coefficients
Eigen::VectorXd b(m); // the right hand side-vector resulting from the constraints
buildProblem(coefficients, b, n);
SpMat A(m,m);
A.setFromTriplets(coefficients.begin(), coefficients.end());
// Solving:
Eigen::SimplicialCholesky<SpMat> chol(A); // performs a Cholesky factorization of A
Eigen::VectorXd x = chol.solve(b); // use the factorization to solve for the given right hand side
// Export the result to a file:
saveAsBitmap(x, n, argv[1]);
return 0;
}

稀疏矩阵和向量声明
SparseMatrix<std::complex<float> > mat(1000,2000); // declares a 1000x2000 column-major compressed sparse matrix of complex<float>
SparseMatrix<double,RowMajor> mat(1000,2000); // declares a 1000x2000 row-major compressed sparse matrix of double
SparseVector<std::complex<float> > vec(1000); // declares a column sparse vector of complex<float> of size 1000
SparseVector<double,RowMajor> vec(1000); // declares a row sparse vector of double of size 1000

稀疏矩阵的填充（赋值）
typedef Eigen::Triplet<double> T;
std::vector<T> tripletList;
tripletList.reserve(estimation_of_entries);
for(...)
{
// ...
tripletList.push_back(T(i,j,v_ij));
}
SparseMatrixType mat(rows,cols);
mat.setFromTriplets(tripletList.begin(), tripletList.end());
// mat is ready to go!

稀疏线性求解器

1、  直接法

 

 

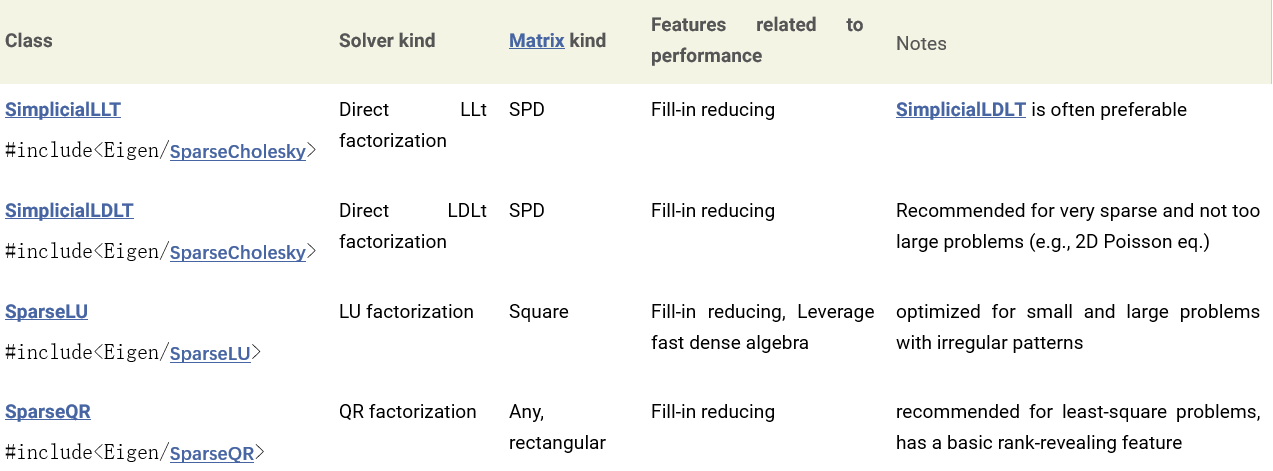
2、  迭代法