霍夫变化后 直线融合算法实现

基于opencv 霍夫变化后 直线融合：

int HoughLinesDB::linesProcess(const vector<Vec4f> &lineVector, double & disThreshold, vector<db::HoughLine> & finalLineVector)
{
    vector<db::HoughLine> lineVector000;
    vector<db::HoughLine> lineVector001;
    for (size_t i = 0; i < lineVector.size(); i++)
    {
        db::HoughLine lineTemp;
        cv::Point p1, p2;

        p1.x = lineVector[i][0];
        p1.y = lineVector[i][1];
        p2.x = lineVector[i][2];
        p2.y = lineVector[i][3];

        pointsGetLines(p1, p2, lineTemp);
        lineVector000.push_back(lineTemp);
    }
    lineVector001 = lineVector000;

    vector<int> lineIndex;  //踢出局
    ///vector<db::HoughLine> finalLineVectorTemp;
    for (size_t i = 0; i < lineVector000.size(); i++)
    {
        if (isExistIndex(i, lineIndex)==1)
            continue;

        db::HoughLine lineTempA;
        lineTempA= lineVector000[i];

        for (size_t j = i+1; j < lineVector001.size(); j++)
        {
            if (isExistIndex(j, lineIndex)==1)
                continue;

            int  mergeMode;
            if (isMergeLine_2(lineTempA, lineVector001[j], disThreshold, mergeMode) == 1)
            {
                lineIndex.push_back(j);   //踢出局

                std::vector<double> kb;
                double  ktemp;
                double btemp;
                ktemp = (lineTempA.k + lineVector001[j].k) / 2;
                btemp = (lineTempA.b + lineVector001[j].b) / 2;
                kb.push_back(ktemp);
                kb.push_back(btemp);

                //int getmax(double x1, double x2, double x3, double x4)
                cv::Point footPoint01, footPoint02, footPoint03, footPoint04;

                footPoint01 = getFootPoint(kb, lineTempA.firstPoint);
                footPoint02 = getFootPoint(kb, lineTempA.endPoint);
                footPoint03 = getFootPoint(kb, lineVector001[j].firstPoint);
                footPoint04 = getFootPoint(kb, lineVector001[j].endPoint);

                std::vector<cv::Point> footPointVector;
                footPointVector.push_back(footPoint01);
                footPointVector.push_back(footPoint02);
                footPointVector.push_back(footPoint03);
                footPointVector.push_back(footPoint04);

                int xmax = getmax(footPoint01.x, footPoint02.x, footPoint03.x, footPoint04.x);
                int xmin = getmin(footPoint01.x, footPoint02.x, footPoint03.x, footPoint04.x);

                lineTempA.firstPoint = footPointVector[xmax - 1];
                lineTempA.endPoint = footPointVector[xmin - 1];
                lineTempA.k = ktemp;
                lineTempA.b = btemp;
            }

        }

        finalLineVector.push_back(lineTempA);
    }

    return 0;
}

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

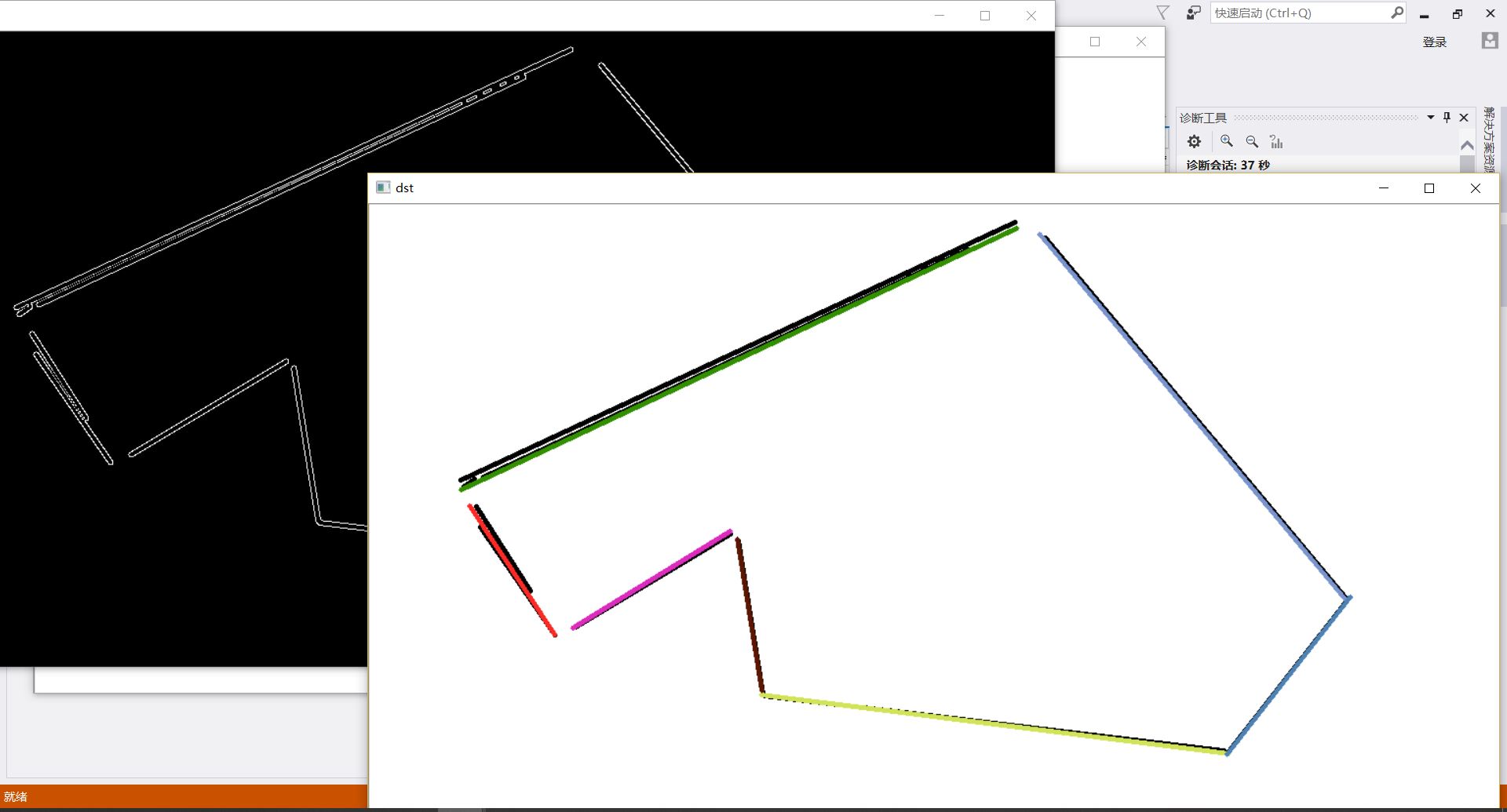
总结：利用“线段自优化”的思想。