物联网前沿实践【3】— 傅里叶分析

在这一章我终于知道了信号的概念——一个关于时间的函数。这个真的很重要，我一直以为信号指的就是一段波，不管在时域还是频域，亦或者是物理上的波，都可以叫信号，可能那也是一个广义的定义吧，大家都这么叫，没有问题。

 当然，在傅里叶得出这个结论时，并没有严格地设定好这个结论成立的条件，狄利克雷补充了这些条件，即傅里叶展开需满足以下条件：

 而绝大部分工程问题遇到的都是有限的问题，因此大部分都可以通过傅里叶展开来解决问题。

我们举一个例子，比如有一个正弦波：

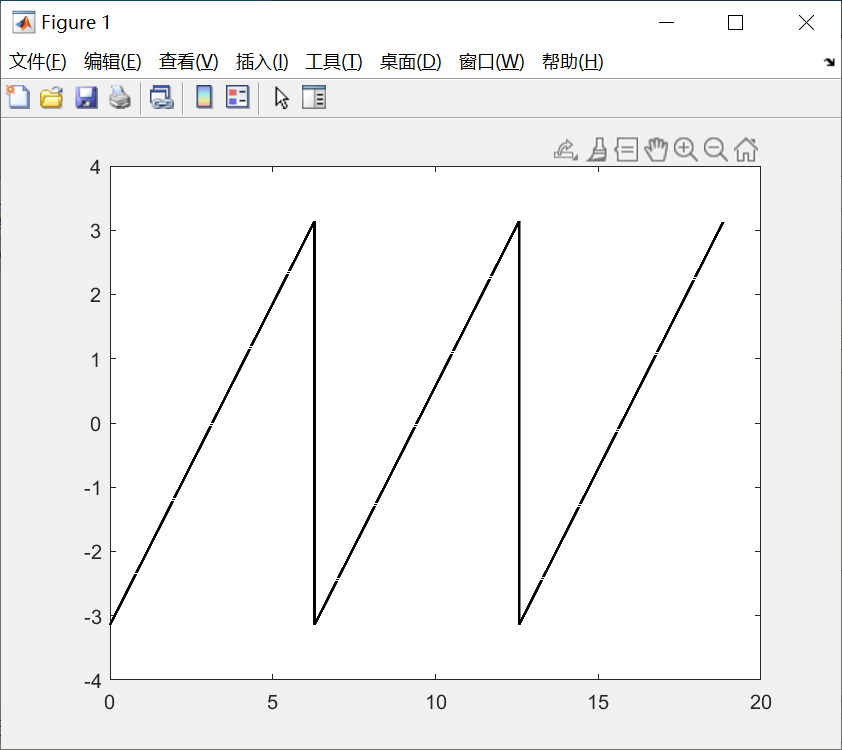
 我们可以选择一个函数来逼近他：

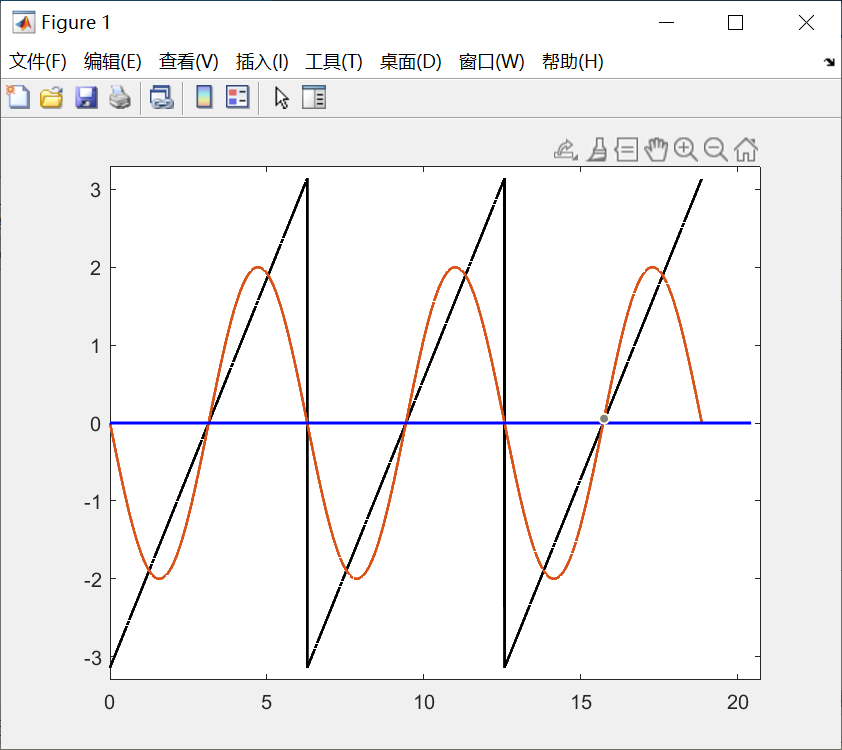
 当然我们可以继续叠加：

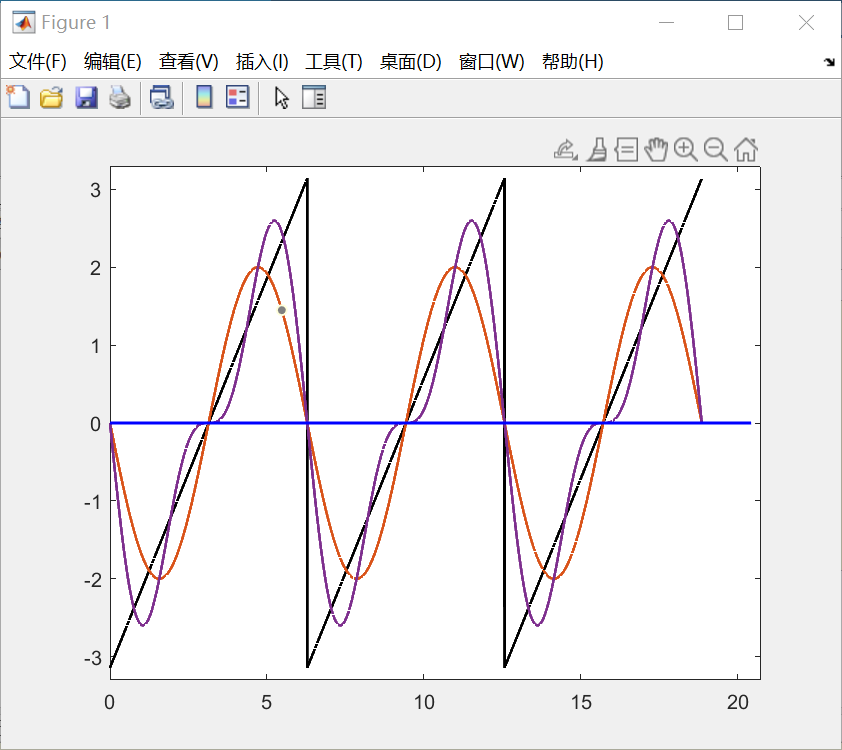
 继续叠加，使得三角函数越来越逼近于所给函数：

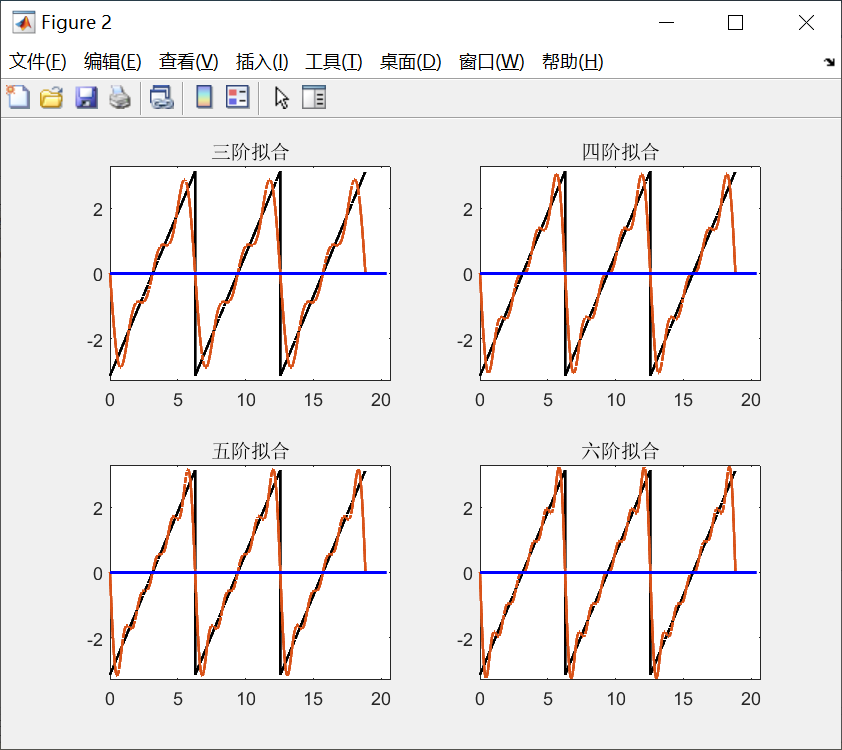
 代码如下：

%% 为了证明任何函数都能用三角函数展开
%% 原始信号：周期为2pi的锯齿形波
% 傅里叶老师是在热力学公式中找到的傅里叶展开式端倪，具体热传导方程的推导过程并不是我们的重点。
% 我们直接看傅里叶老师的断言：所有函数都可以用三角函数叠加得到，为此，我们来模拟一个，哪怕是不连续的锯齿波
fs = 1e3;
t = 0:1/fs:6*pi;                                           % fs代表了步长
y = -pi + mod(t,2*pi);
figure;
plot(t,y,'color','black','linewidth',1.5);

%% 使用最小周期为2pi的基础正弦波sin(x)拟合锯齿波
z = -2*sin(t);
hold on
plot(t,z,'linewidth',1.5);
plot([0,6.5*pi],[0 0],'color','blue','linewidth',1.5);              % 注意这个函数是画一条线而已
xlim([0,6.6*pi]);
ylim([-3.3 3.3]);
box on

%% 叠加最小周期为pi的基础正弦波sin(2x)做二阶拟合
z = -2*sin(t) - sin(2*t);
hold on
plot(t,z,'linewidth',1.5);
plot([0,6.5*pi],[0 0],'color','blue','linewidth',1.5);
xlim([0,6.6*pi]);
ylim([-3.3 3.3]);
box on

%% 不同阶数三角函数叠加结果示意
figure;
z = -2*sin(t) - sin(2*t) - 2/3*sin(3*t);
subplot(2,2,1);fplot(t,y,z);
title('三阶拟合');

z = -2*sin(t) - sin(2*t) - 2/3*sin(3*t) - 1/2*sin(4*t);
subplot(2,2,2);fplot(t,y,z);
title('四阶拟合');

z = -2*sin(t) - sin(2*t) - 2/3*sin(3*t) - 1/2*sin(4*t) - 2/5*sin(5*t);
subplot(2,2,3);fplot(t,y,z);
title('五阶拟合');

z = -2*sin(t) - sin(2*t) - 2/3*sin(3*t) - 1/2*sin(4*t) - 2/5*sin(5*t) - 1/3*sin(6*t);
subplot(2,2,4);fplot(t,y,z);
title('六阶拟合');

function fplot(t,y,z)
hold on;
plot(t,y,'color','black','linewidth',1.5);
plot(t,z,'linewidth',1.5);
plot([0,6.5*pi],[0 0],'color','b','linewidth',1.5);
xlim([0,6.6*pi]);
ylim([-3.3 3.3]);
box on;
end



%%
% x=-3:1/1000:3
% y=2*x+2;
% plot(x,y,'linewidth',10,'color','black');
% % plot([0,5],[-4 4],'color','blue','linewidth',4);

%%

 

 讲道理，傅里叶级数展开的公式我仍然是看不懂的……我只是单纯地从普通的直觉上理解了它在干什么，随用随理解吧，这个东西我觉得需要时间沉淀。

一个很不错的傅里叶变换简单介绍：https://mp.weixin.qq.com/s?__biz=MzU0MDQ1NjAzNg==&mid=2247545607&idx=1&sn=590e4a13099851a6b33b5694386442f9&chksm=fb3a960ccc4d1f1a769660174d24e14761168c38e9e413372a6a5637af301a8897271eeba31a&scene=27

3b1b的傅里叶变换：https://www.bilibili.com/video/BV1pW411J7s8/?spm_id_from=333.337.search-card.all.click&vd_source=d0edf1d3f760c41c638551d47a67826e

 其中让我非常眼前一亮的故事，就是3b1b的“质心”的引入，用这个来理解傅里叶变换是怎么得到频域的就非常直观。

接下来是一组简单的傅里叶变换demo，对一个正弦函数做傅里叶变换：

%% 傅里叶分析信号
fs = 1e3; % 采样率1000Hz

% 构造频率为100Hz的正弦波
f0 = 100;
t = (0:1/fs:1/f0-1/fs)'; % 采样一个周期
% t = (0:1/fs:5/f0-1/fs)'; % 采样五个周期
xn = sin(2*pi*f0*t);
N = length(xn);
disp(N) %在采样一个周期的时候等于10，因为采样率是1000HZ，频率为100Hz，采样比频率快10倍，一个周期采样10个点
figure('Position', [200 200 1400 300]);
subplot(131);
stem((0:N-1)',real(xn),'color','black','linewidth',1.5); % 使用stem函数绘制散点数据图，real()取出了xn的实部
ylim([-1.5 1.5]);
xlabel('时间（ms）');
ylabel('强度');

% 不补零的FFT
yn = fft(xn);
% 将负频率放到左侧
yn = [yn(N/2+1:end); yn(1:N/2)];

% 补零的FFT
r = 16; % 补零倍数
yn2 = fft(xn, r*N);

% 如果我们有一个长度为 N 的输入信号 xn，那么 fft(xn, rN) 的作用是将 xn 补零到 r 倍的 N，得到一个长度为 rN 的新信号，再对这个新信号进行 FFT 变换。

% 补零操作可以增加信号的长度，因此可以增加 FFT 的分辨率。通过增加分辨率，我们可以更准确地检测信号的频率和幅度。

 

% 将负频率放到左侧
yn2 = [yn2(N*r/2+1:end); yn2(1:N*r/2)];

subplot(132);
f1 = (-r*N/2:r*N/2-1)'/(r*N)*fs;
f2 = (-N/2:N/2-1)'/N*fs;
plot(f1, abs(yn2),'color','black','linewidth',1.5); hold on
stem(f2, abs(yn),'color',[0,118,168]/255,'linewidth',1.5,'linestyle','none');
xlabel('频率（Hz）');
xticks(-500:100:500);
ylabel('强度');
ylim([0 1.25*max(abs(yn2))]);
legend('补零', '不补零', 'Location', 'NorthEast');

subplot(133);
f1 = (-r*N/2:r*N/2-1)'/(r*N)*fs;
f2 = (-N/2:N/2-1)'/N*fs;
plot(f1, angle(yn2),'color','black','linewidth',1.5); hold on
stem(f2, angle(yn),'color',[0,118,168]/255,'linewidth',1.5,'linestyle','none');
xlabel('频率（Hz）');
xticks(-500:100:500);
ylabel('相位');
ylim([-5 5]);
legend('补零', '不补零', 'Location', 'NorthEast');

 运行一下：

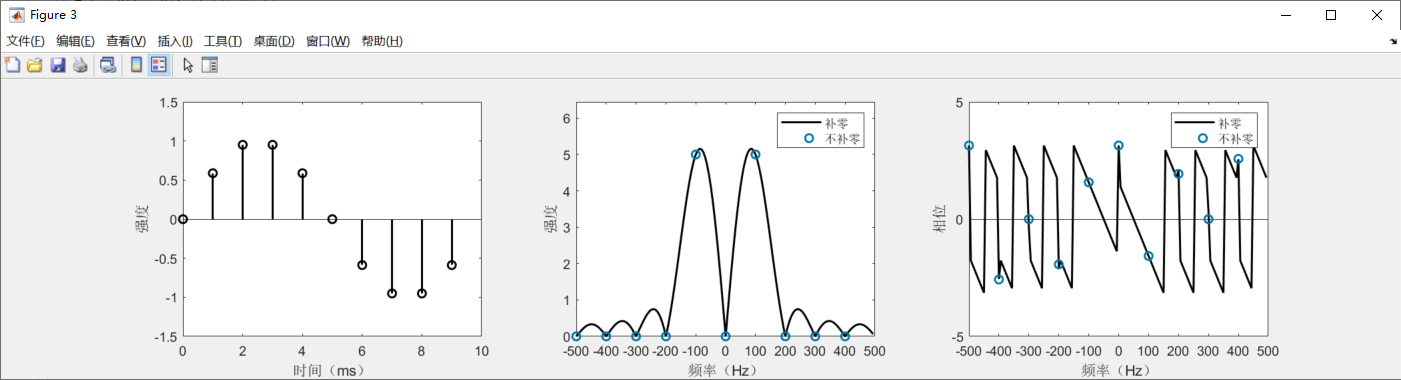
 与此同时，我们也跑出采样5个周期的图：

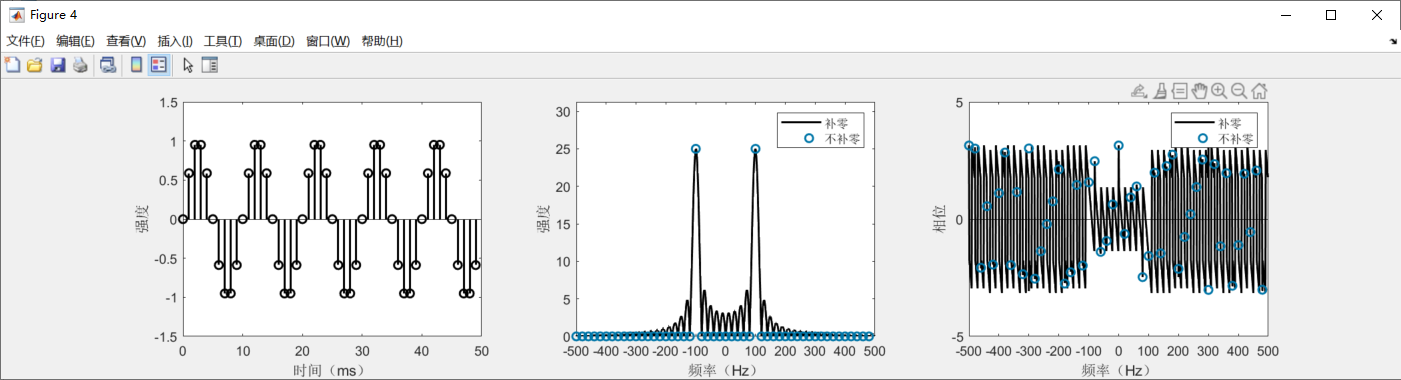
 其中比较值得在意的就是频谱图，补零和不补零对还原的信号信息有所差异。

 补零可以增加信号的分辨率，从而使得信号更好地拟合原始信号，在一个周期的例子里，没有补零的图告诉我们只有100Hz信号，然而16倍补零后的图告诉我们它还有别的信号，这就是补零的好处。

然而补零不能乱补，

 

 

 

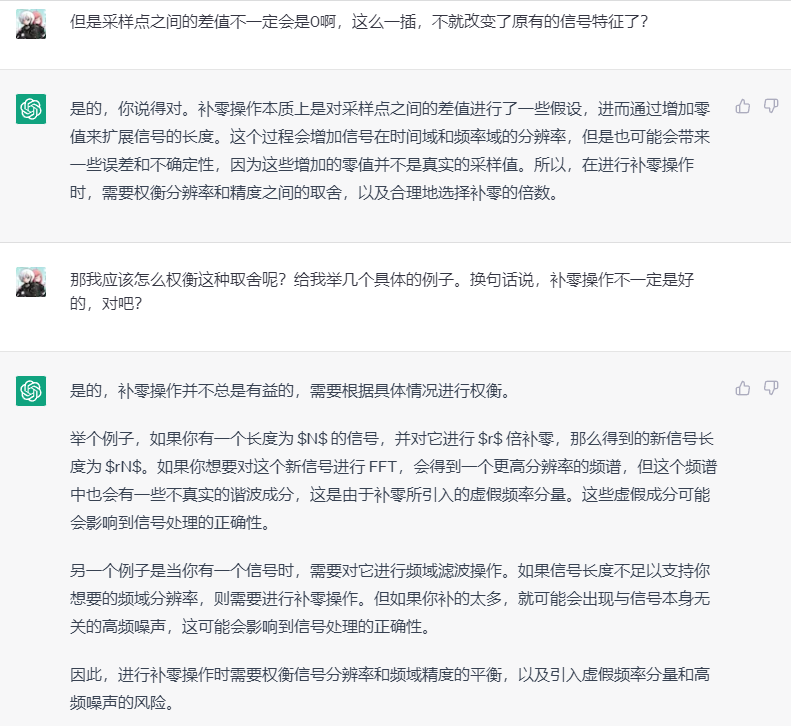
图中一个奇怪的现象是，当我们只采样了一个周期的信号时，未补零的频谱告诉我们信号中只含有100100Hz的频率，补了16倍零的更细粒度的频谱却告诉我们最大成分的频率并非100100Hz（蓝色圆圈与黑色曲线最高点明显不重合）。这是为什么呢？因为在FFT看来，一个实数正弦波包含有两个频率，分别是100100Hz和−100−100Hz，由于信号的有限性，这两个频率会产生旁瓣从而互相干扰，于是原本应指向100100Hz的峰被扰动偏移了。这个效应会随着旁瓣的变小而趋弱。

抑制旁瓣在实际信号处理中非常重要，一般抑制旁瓣有两种方法，其一是给信号乘上一个窗函数，俗称“加窗”。“加窗”的过程在很多工作中包括论文中都被有意无意的忽略了，或者就不讲了，实际上很多情况窗函数的使用能够极大的简化信号处理的难度，甚至能对效果起到决定性的作用，在信号加窗之前，对信号进行一定的预处理，使其在时间或频率上有一定的平滑性。窗函数主要有矩形窗、汉宁窗、汉明窗等。。另一种方法是延长采样时间（让我们的信号不再“有限长”）。由图可知，在我们加长采样时间到五个周期时，黑线的尖峰终于近似和蓝色圆点重叠，我们从频谱读到了100100Hz频率。

当然了还有别的方法，就是类似补零的操作。当然了，也有滤波操作，直接滤掉不需要的波。

 

但是，上面是对于完整周期的波形做的分析，如果对于非完整周期截断的正弦波进行分析呢？

 这种失真就会变得非常明显，因此这个时候不得不补零操作。

 

 

 

 

留白