TI的FMCW毫米波雷达培训笔记1：FMCW基本原理以及如何测量不同距离的物体的距离（雷达小白知识点整理）
参考：
培训地址：https://training.ti.com/mmwave-training-series
Indish翻译Chinese：https://www.bilibili.com/video/BV1tE411j7vT
一篇蛮不错的傅里叶变换通俗理解：https://blog.csdn.net/l494926429/article/details/51818012/
一、一些基本概念
FMCW（Frequency Modulated Continuous Wave）：调频连续波，其核心是线性调频脉冲信号（chirp），即频率随时间增长的正弦波，A-t图如下：
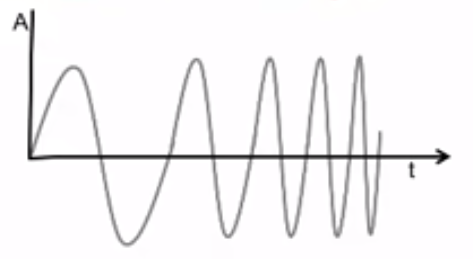
加速度与时间图像（a-t图像）有如下几个特点：
1、意义：反应了物体加速度随时间变化的规律。
2、如果图像平行于t轴，表示物体做匀变速直线运动；如果图像是曲线或倾斜的直线，表示物体做变加速度运动。
3、图像在第一象限，表示物体加速度方向为正方向；图像在第四象限，表示物体加速度方向为负方向。
4、图像与t轴围成的面积表示为物体速度变化量，面积在第一象限表示物体速度在正方向上的增加量，面积在第四象限表示物体速度在负方向上的增加量。
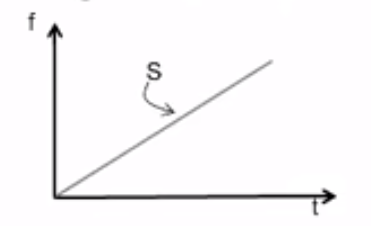
其中，这个正弦波的频率由小变大，假设以fc开始，到fc+B结束，那么B就是调频脉冲的带宽。这是一个线性过程，在频率-时间图中就是一条斜率为S的直线。
线性调频脉冲本质上是频率以线性方式进行调制的连续波，这就是FMCW名字的来源。
给上面的那个图加上一些数字，如下图：
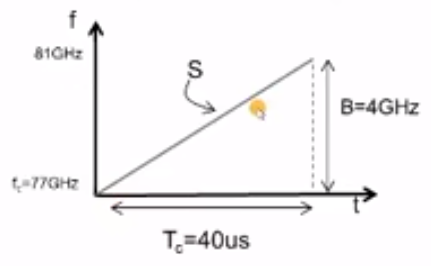
该图就表示，以77GHz的频率开始跨越 4GHz带宽最终以81GHz结束的波，其中S决定了这个波频率的增长速度。其中，B和S是定义整个系统的最重要的两个参数。
二、一个雷达测量距离的工作机制
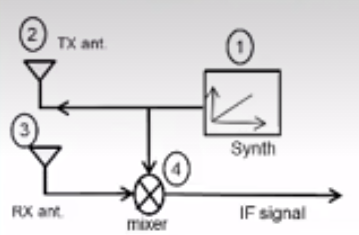
如上图，首先由一个生成器生成波，随后用一个发射天线（TX）发射出去，再用接收天线（RX）接受回来，将两个波都输入到一个mixer中，生成IF信号。
IF信号具有两个特性，即频率为输入信号之差，相位为输入信号之差。
即：x=sin[(w1 - w2)t +(φ1- φ2)]
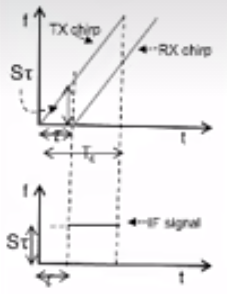
那对于TX和RX天线的波，可以表示在一个f-t图中，二者之差，即为IF signal，前面的τ即为接收延迟，即波一个来回的时间，那让这个时间乘以光速再除以2，就是物体距离雷达的距离d。那么，这个IF信号的频率就等于S2d/c，因为τ=2d/c。
需要注意的是，这个τ相对于整个时间段来说，可能非常小。
而对于多个物体而言，也是同样的，如下：
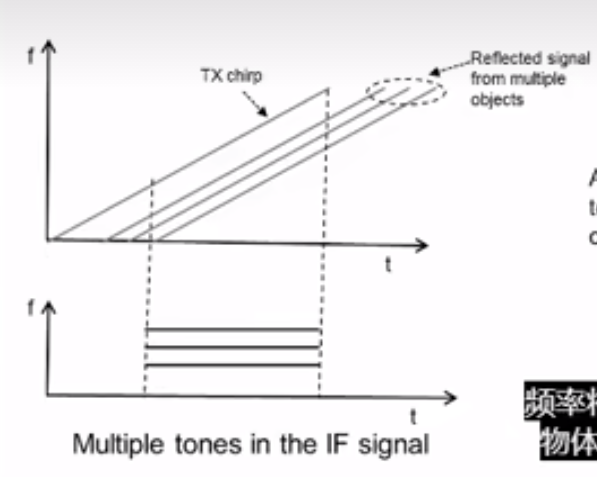
TX发出了一个波，RX接受了三个，但是三个波延迟不同，所以我能产生三个IF信号，而IF的频率与雷达与物体的距离成正比，因此最上面的就是最远的物体。此图画的有点问题，f-t函数的起点不应该相同，远距离的τ肯定要大于近距离的τ。
傅里叶变换能将IF信号转换成多个峰值，这些都代表不同物体，其中f越大（频率越大），对应的物体离雷达距离越远。
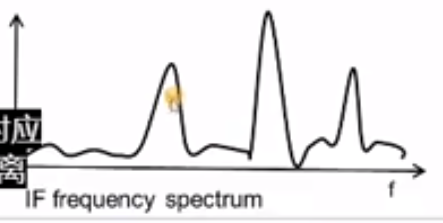
那么，如何分辨两个距离相近的物体呢？或者，雷达的距离分辨率是由什么决定的？
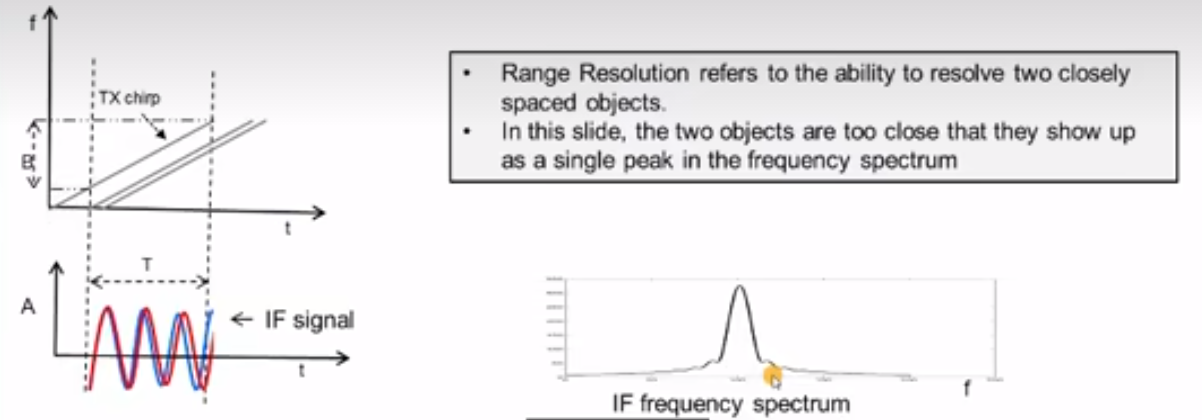
如上图，对于两个距离相近的物体来说，其形成的IF正弦波非常相近，做傅里叶变换后没有办法区分出两个波。比较直观的方案是增大带宽B，如下图：
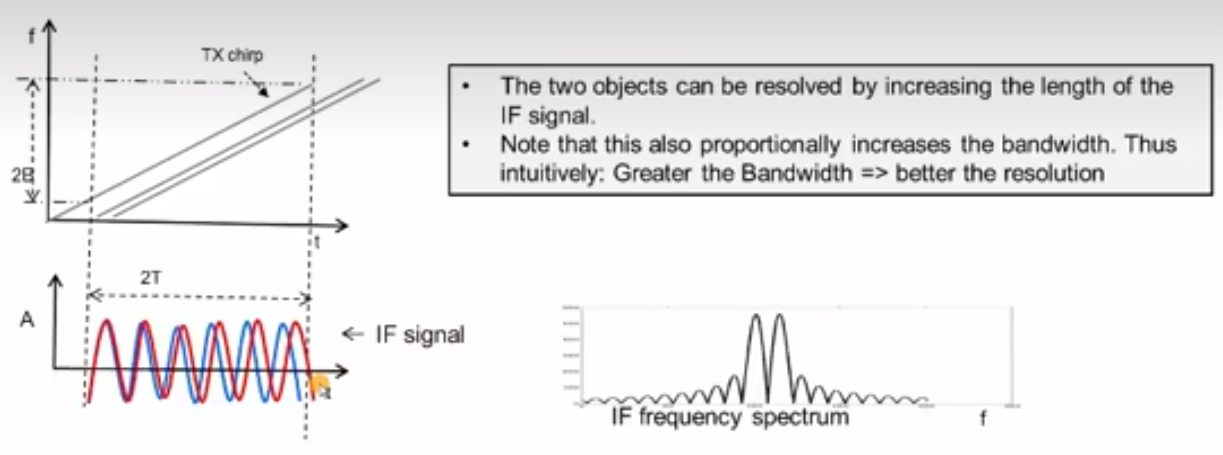
因此我们说，正常情况下，更大的带宽对应更好的距离分辨率。
用公式表示就是：二者的距离必须大于光速除以两倍的带宽。
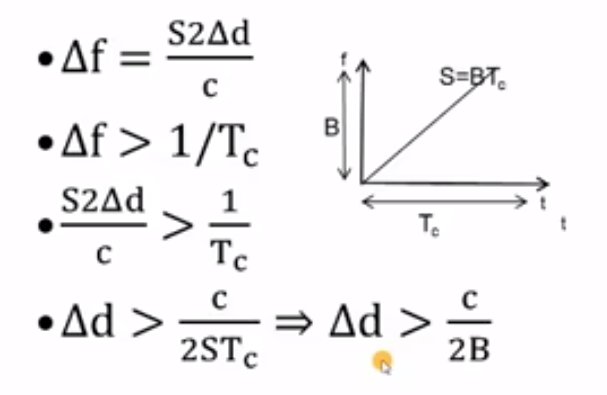
（这里这个第二行的不等式还不理解，慢慢来用到再说）
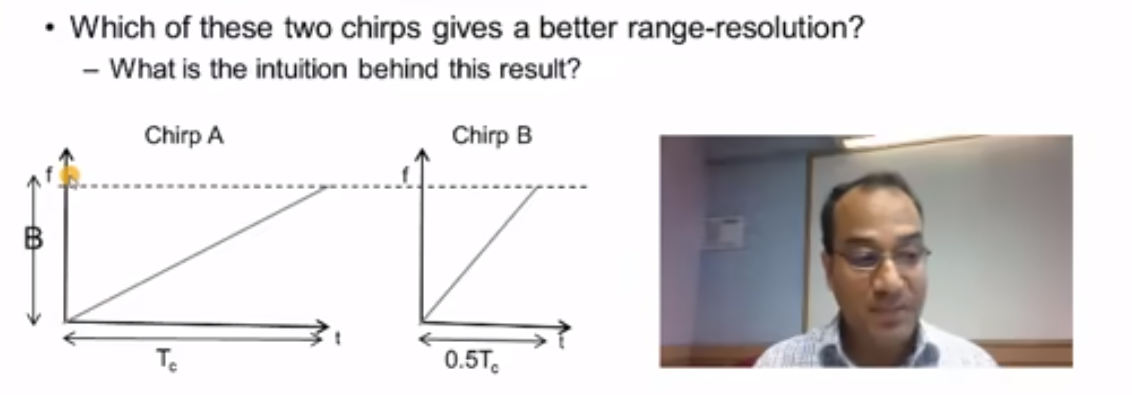
那么，对于下面的例子来说，具有相同带宽的两个chirp肯定具有相同的距离分辨率。但是A生成的IF信号窗口更大一些。
三、IF信号的数字化机制
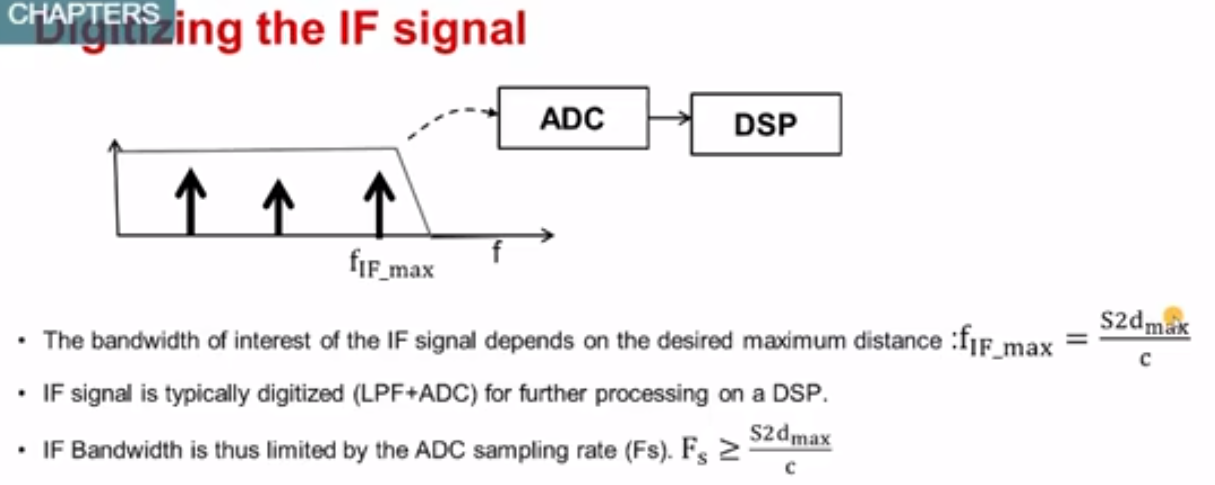
在数字化之前，我们首先要明确我们到底有多大带宽，对哪段距离的物体感兴趣。
首先通过一层低通滤波，滤掉dmax以外的物体，我们不感兴趣，所以设置一个fIF_max；而ADC的采样率也应该高于此最高频率（如果采样率比频率低那将不可描述）
可以看到，带宽取决于斜率与最大距离乘积；如果ADC的采样率或者带宽B是任务雷达的瓶颈，那么我们可以平衡斜率S和最大距离dmax。现实中往往倾向于更大的dmax和更小的S。
对于第二章两个chirp例子A和B，就是折中的部分，即二者带宽相同，A的S更小，那么A就能够获取更大的dmax，相对来说，比起chirpB对带宽B的要求更加宽松；但是B的优势在于时间短，这就是需要考量折中的部分。
大致总结一下：
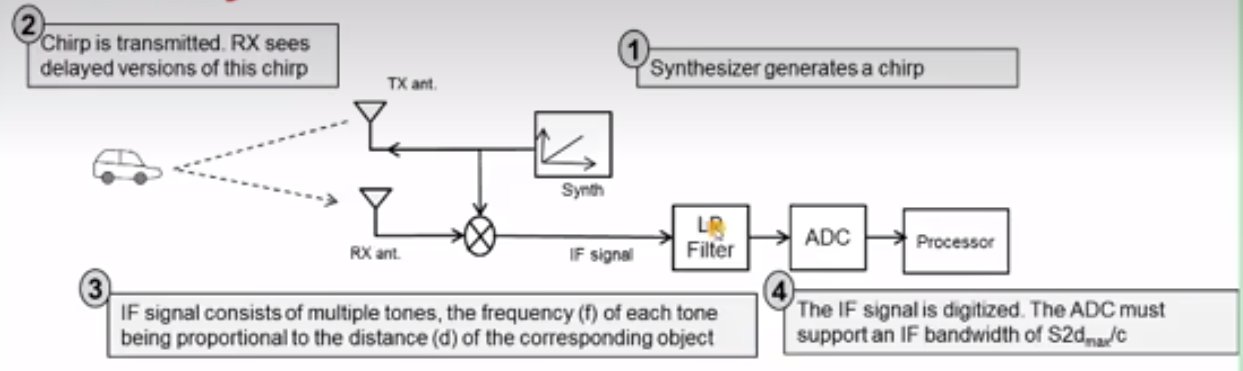
1、生成器生成一个chirp，交给TX天线；
2、TX把这个chirp发送出去，在物体返回过来之后，由RX天线接收；
3、对获取的两个chirp进行mix，得到IF Signal
4、通过低通滤波之后的IF Signal，可以被一个ADC数字化，然后输入到处理器中。
总之，今天主要讲的是FMCW如何检测物体距离以及区分不同距离的物体。后序更加有挑战性的工作，我们下篇再见~
第二期：https://www.cnblogs.com/loveandninenine/p/16818575.html
