20220219读“精读PointNet” 以后每个月做一次问题规整，每个月月底传一次问题集

PointNet论文精读：https://blog.csdn.net/cg129054036/article/details/105456002

3D点云深度学习：https://blog.csdn.net/kkxi123456/article/details/102731709

三维点云网络PointNet的模型与代码解析：https://blog.csdn.net/u014636245/article/details/82763269

 

对于点云，我们想要用神经网络去处理它。

点云是数据的表达点的集合，网络模型对于这些表达点的排列应该是不敏感的。

但是，对于一个有N个点的点云集合，它的排列方式有N！种，那么对于这N！种点的排列方式，我们的网络模型输出的内容应该是一致的。

神将网络本质上是一个函数，我们希望找到一个对称函数，能够对于点云数据具有置换不变性。如取最大值函数，无论输入怎么变换，最后的结果都是输入的最大值。

这里的置换不变性，英文叫Permutation Invariant，Google查到的解释如下（https://stats.stackexchange.com/questions/120089/what-does-permutation-invariant-mean-in-the-context-of-neural-networks-doing-i）：

 

 

 

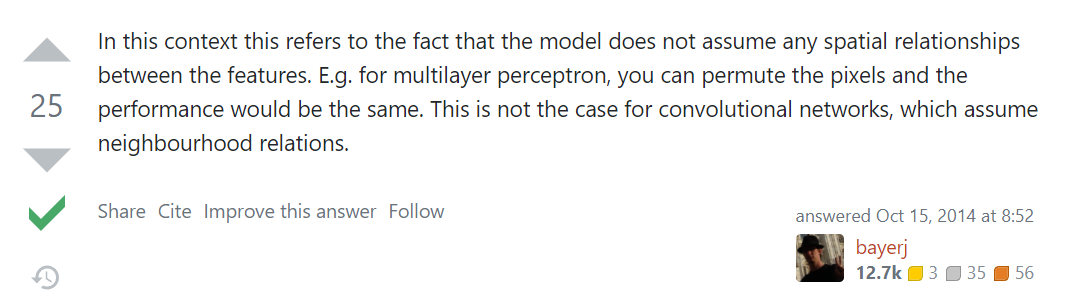
 也就是说，对于一个模型，特征不应该存在任何空间上的联系。

T-Net：学习出变化矩阵来对输入的点云或特征进行规范化处理。

 

可以先把每个点映射到高维空间，在高维空间中做对称性的操作，高维空间可以是一个冗余的，在max操作中通过冗余可以避免信息的丢失，可以保留足够的点云信息，再通过一个网络来进一步消化信息得到点云的特征。这就是函数的组合：每个点都做h低维到高维的映射，G是对称的那么整个结构就都是对称的。下图就是原始的pointnet结构。

这段话没有看太懂，为什么高维空间能够这样保证对称？

我们发现，pointnet 可以任意的逼近在集合上的对称函数，只要是对称函数是在hausdorff空间是连续的，那么就可以通过任意的增加神经网络的宽度深度，来逼近这个函数

为什么要在hausdorff空间保持对称函数连续？