深度学习笔记026 ResNet 残差网络
沐神:如果你在神经网络中要了解一个网络的话,一定就是要了解ResNet网络了。
在这里首先要思考一个问题:

显然不一定,就如左图所示,我们的模型从F1这么小个训练到了F6这么大个,可能的最优解却变得更差了,这就是所谓的一条路走到黑。
这里的计算涉及到泛函的知识,之前没接触过,感觉挺大一块,慢慢用到在学,现在先不学了。
这里要区分一下过拟合和这个一条路走到黑(训练跑偏)的区别:
训练跑偏指的是,模型越训练,自己能够得到的最好的解离最优解越远;
过拟合指的是自己得到的值太过靠近训练集的最优解。
ResNet的思想就是,加更多的层,不会让网络变差,通常来说只会让网络变小。
用公式来说,就是f1(x) = f(x) + g(x) # f(x)是原网络上一层的输出,也就是接下来的输入;g(x)是新加入的网络,如下:

换句话说,我这个ResNet允许你可以嵌入其他的小网络。
而所谓的残差块,就和别的什么VGG块啊Inception块啊之类的都不一样了,这里的残差块都是小网络,什么网络都可以,LeNet,AlexNet都可以,直接接上来就行,只不过接上来之后需要再通一条输入数据,让两者相加送入下面的网络,这样就不会改变小原来模型的范围。
当然了,经典的ResNet,是有一个属于自己的ResNet块的,就是下图虚线框,经典的ResNet是将下图虚线框重复了多次。
通出来的一条路,常常要加入一个1x1卷积层来改变通道数,因为新加的网络块可能会改变数据的通道数。
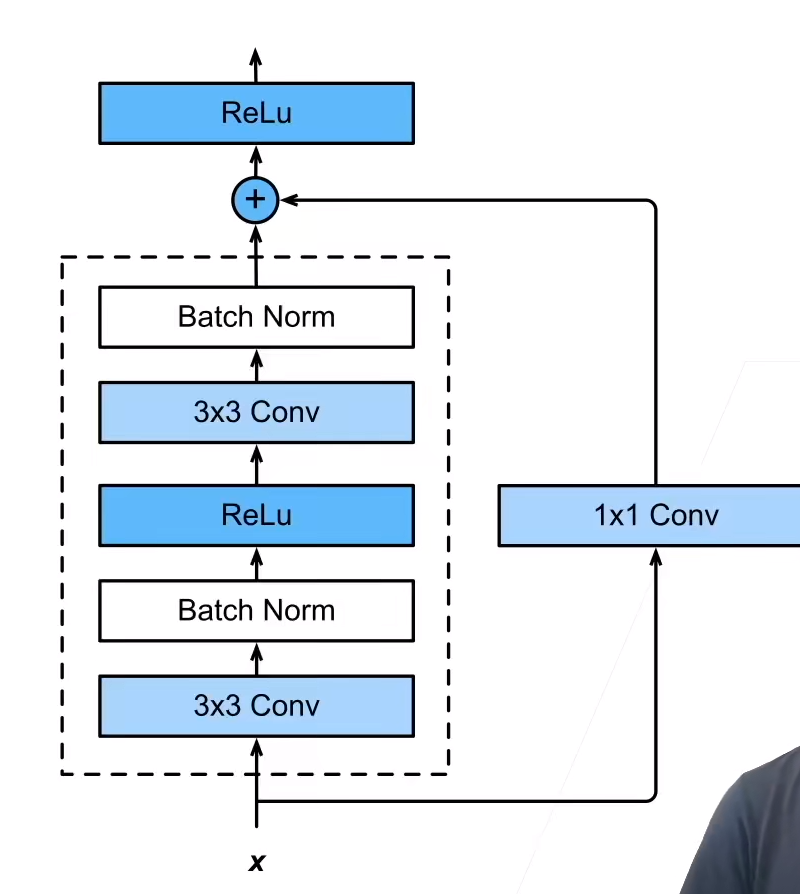
总结:
残差块使得很深的网络更加容易训练(甚至可以训练一千层的网络)
残差网络对随后的深度神经网络设计产生了非常深远的影响,无论是卷积类网络还是全连接网络。
结果
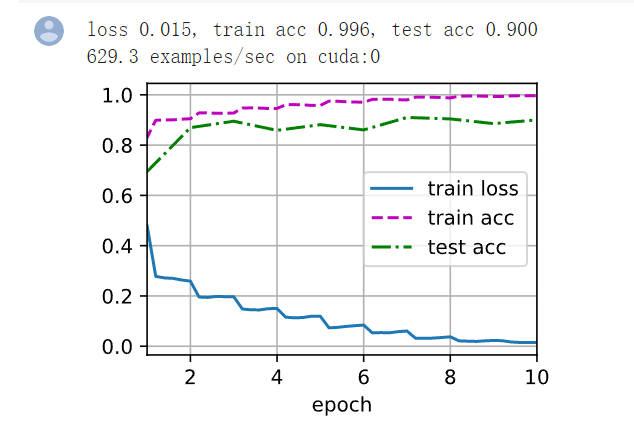
可以看到,10个epoch将训练数据的准确率提升到了99.6%!怪不得沐神总说“你要学卷积神经网络就学ResNet就可以了”,这特奶奶的是真的牛逼。当然了,出现了很严重的过拟合,但这正是证明这个模型复杂度足够,且学习能力很强的标志,剩下的就是解决过拟合问题,一点点降低模型复杂度就行了。
之前觉得GoogLeNet是集大成者,其实并不是,GoogLeNet也只不过是缝合怪罢了,只是GoogLeNet提出了一个很重要的方法,就是分路分通道训练,这个思想是一个从零到一的过程,非常棒;而ResNet相对于GoogLeNet,就是不像GoogLeNet那样分那么多条路,而是只有两条路,一条路随便走,另一条路是空路或者只有一个1x1卷积,这样能够真正地做到缝合一切而且结果只会变好,最差是不变,但绝对不会让任何一个网络起到反作用,牛逼!
另外,Residual如何处理1000层的梯度?

Q&A
1、f(x)=x+g(x),g(x)也是训练的,如果模型发现gx训练效果很差,一般拿不到什么梯度,做梯度反传的时候是很小的梯度,甚至是0,所以如果g对于整个模型没有啥贡献的话,他也起不到什么作用,因为权重太小了。
2、“残差”二字体现在训练上。上一层训练的网络精度不太够由这一层继续精化,这两层的差距就是残差,这个残差由本层来拟合。
3、很多数据集有一种样例,叫hard case,就是说人看都模棱两可,不能确定真正的种类。
4、学习率可以让靠近输出的小一些,靠近输入的大一些,这样可以缓解梯度消失的问题,但是这具体的学习率如何取值,很困难。
5、梯度是累乘,累乘到底层的时候梯度已经很小了,所以很难训练。因为这个问题,过去几十年在深度神经网络这一块一直做的不太好。
代码
import torch from torch import nn from torch.nn import functional as F from d2l import torch as d2l # 残差块 class Residual(nn.Module): def __init__(self, input_channels, num_channels,use_1x1conv=False, strides=1): #输入通道数,输出通道数,是不是用1x1卷积,是的话步长是多少 super().__init__() # 两个卷积 self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1, stride=strides) self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1) # 1x1卷积层,把通道数整理好 if use_1x1conv: self.conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=1, stride=strides) else: self.conv3 = None # 两个BN self.bn1 = nn.BatchNorm2d(num_channels) self.bn2 = nn.BatchNorm2d(num_channels) def forward(self, X): Y = F.relu(self.bn1(self.conv1(X))) Y = self.bn2(self.conv2(Y)) if self.conv3: X = self.conv3(X) Y += X return F.relu(Y) # 假设输入输出通道数都规定为3,那么输出就一直是一样的,可以做个实验: blk = Residual(3,3) X = torch.rand(4, 3, 6, 6) Y = blk(X) Y.shape # 相反的,通道数加倍,一般我们就认为高宽减半,所以步长可以设为2 blk = Residual(3,6, use_1x1conv=True, strides=2) blk(X).shape # ResNet的前两层跟之前介绍的GoogLeNet中的一样: 在输出通道数为64、步幅为2的 7×7 卷积层后,接步幅为2的 3×3 的最大汇聚层。 不同之处在于ResNet每个卷积层后增加了批量规范化层。 b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3), nn.BatchNorm2d(64), nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) # 之前写的残差块可以认为是ResNet的一个循环块,而这里这个可以认为是一个stage def resnet_block(input_channels, num_channels, num_residuals,first_block=False): # 输入输出的通道数,我们需要多少个循环,以及是不是第一个stage blk = [] for i in range(num_residuals): # 这里我们将接下来要连接的第一块网络做一个特判,也就是下面的b2层,因为之前的卷积和池化已经减半了两次,所以第一层不减半了,后面的每个stage再各减半一次即可 if i == 0 and not first_block: blk.append(Residual(input_channels, num_channels, use_1x1conv=True, strides=2)) else: blk.append(Residual(num_channels, num_channels)) return blk b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True)) # *的意义是把list展开逐一输入 b3 = nn.Sequential(*resnet_block(64, 128, 2)) b4 = nn.Sequential(*resnet_block(128, 256, 2)) b5 = nn.Sequential(*resnet_block(256, 512, 2)) net = nn.Sequential(b1, b2, b3, b4, b5, nn.AdaptiveAvgPool2d((1,1)), nn.Flatten(), nn.Linear(512, 10)) X = torch.rand(size=(1, 1, 224, 224)) for layer in net: X = layer(X) print(layer.__class__.__name__,'output shape:\t', X.shape) lr, num_epochs, batch_size = 0.05, 10, 256 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96) d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())




