线性回归原理

线性回归简介

绘制一条 函数曲线 要求是 尽量去符合 观测到的值

观测到的 x 和 y

把x带入到 我们 假设的函数中 得到y_

y-y_

y = w*x+b

w 是 斜率 也可以认为是权重 weight
b 是 截距 也可以认为是偏差 bias

图解

先来看两张图

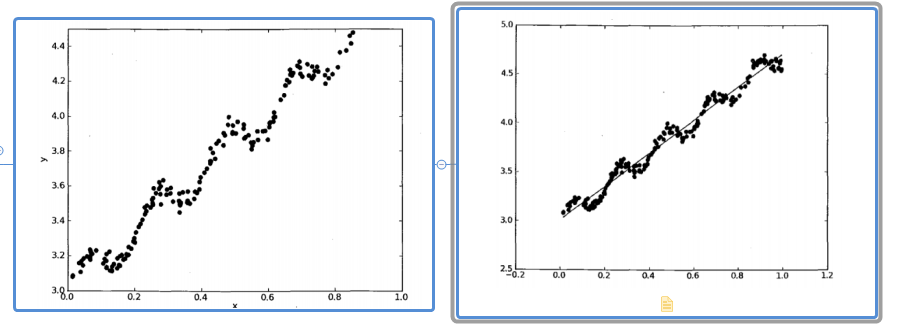
左边这张是样本各个点的数据集，那么我们利用机器学习的线性回归模型绘制出来的如右图所示。

根据已有的点 通过调整w和b的值 让损失函数（所有预测值和真实值之间差值的平方和）的值最小，这就是线性回归做的事情。

梯度下降算法

可见上式是一个二次方程,那么它的函数曲线就是一个有开口的,有对称轴的曲线

梯度下降的原理就是在曲线上取任意点,对所在点的位置求导得到k,代入下式中

position - a *k

 然后移动a*k个单位,若所在点在最小值点的右侧 ,那么它的导数会逐渐的减小,移动的距离也越小

梯度下降的时间空间复杂度都相对比较高,一般应用于有多个特征值的时候使用.

最小二乘法

(X*w-y)^2 想要获得这个公式的极小值 需要求导并零导数为0
注意: 这里的变量是w（我们想知道的是什么样的w能够使得 函数有最佳拟合）

# 求导
(X*w-y)^2
2(X*w-y)*X = 0
注意:这里是一个复合函数的求导# x^2 a*x+b

求导后得:

X*w=y

这里的X是一个矩阵,要计算矩阵就不能简单的把X除过去了,必须要求得X的逆矩阵,通过逆矩阵与X做点乘得1,把X消去求得w

那么首先要确保 做 逆矩阵的 矩阵 是方阵 才可以求逆矩阵

所以要乘以X的转置(任意矩阵和自己的 转置矩阵 相乘 得到的是一个方阵)
(X.T*X)^-1*X.T*X*w=(X.T*X)^-1*X.T*y

import numpy as np
X = np.random.randint(0,10,size=(2,3))

array([[4, 1, 2],
       [5, 1, 4]])

X.T  # 行变成 列 就是 矩阵的转置
# 任意矩阵和自己的 转置矩阵 相乘 得到的是一个方阵
np.dot(X,X.T)
# linalg 线性代数 linear algerithm
np.linalg.inv(np.dot(X,X.T))
a = np.array([[21, 29],
       [29, 42]])
b = np.array([[ 1.02439024, -0.70731707],
       [-0.70731707,  0.51219512]])

np.dot(a,b)

# 趋近于1,趋近于0
array([[1.00000001e+00, 1.00000009e-08],
       [2.00000003e-08, 1.00000001e+00]])

得w=(X.T*X)^-1*X.T*y

那么 我们对这个推导出来的公式进行一次测试

2*x1+3*x2=5
1*x1+1*x2=4
1*x1-1*x2=10

x2 = -3
x1 = 7

X = np.array([
    [2,3],
    [1,1],
    [1,-1]
])

y = np.array([5,4,10])

a = np.linalg.inv(np.dot(X.T,X))
b = np.dot(a,X.T)
np.dot(b,y)
得 array([ 7., -3.])

使用机器学习库中的方法计算

from sklearn.linear_model import LinearRegression
lr = LinearRegression()  # 使用模型的构造函数 来创建一个新的模型
lr.fit(X,y)
lr.coef_