题解：P7353 [2020-2021 集训队作业] Tom & Jerry

Problem Link

思考 Tom 怎么获胜，有以下两种情况：

1. Tom 不断限制 Jerry 的活动范围，直到困死。
2. ~Tom 瞎走都可以赢~，有一个点能让 Tom 必胜。

对于（1），显然 Tom 需要不断走割点，由此想到圆方树。

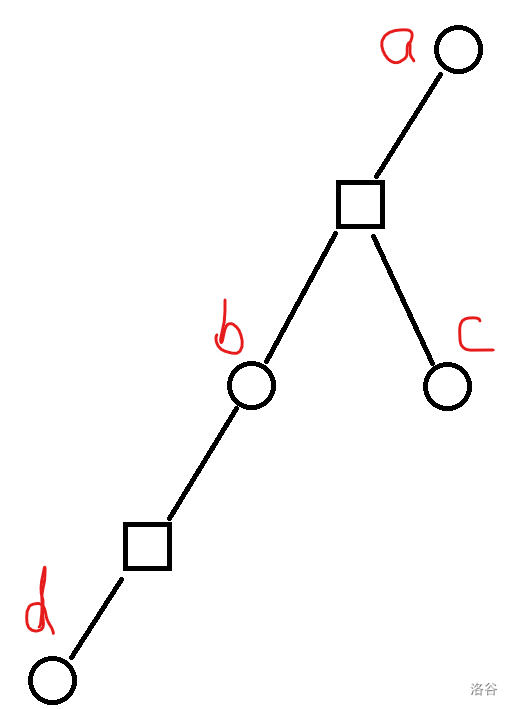
假设 Tom 在 \(a\)，Jerry 在 \(d\)，Jerry 能在 \(a\) 的子树里任意走，所以 Tom 需要让 \(a\) 能直接到达 \(b\) 和 \(c\)，否则就输了。由此看出每当 Tom 在 \(x\)，Jerry 在 \(x\) 的子树 \(y\) 内时，\(x\) 必须直接到达 \(y\) 代表的点双连通分量中的任意点。此时 Tom 必胜。

对于（2），考虑能让 Tom 必胜的那个点 \(x\)，此时 Jerry 可以在任何地方（否则（1）就讨论过了）。Tom 必胜条件就是对于 \(x\) 的任何子树，（1）的条件都成立。

若（1）（2）都不成立，Tom 必败。

接下来实现挺复杂的，我看其他 dalao 题解是没怎么看懂（我太蒻了），这里介绍一下我的写法。

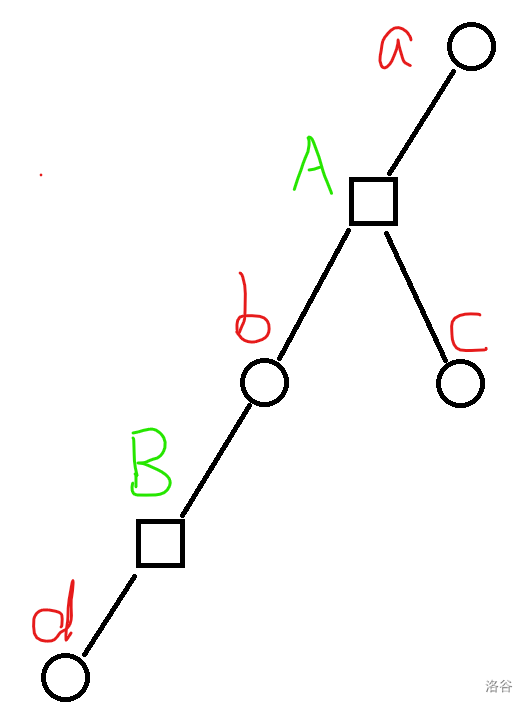
考虑如何表示 \(x\) 能直接到达其点双连通分量的任意点。可以将这个状态放到 \(x\) 到对应方点的边上。

枚举原图上的边，如 \((a,b)\)，则在圆方树上让 \(w(a,A)\) 和 \(w(b,A)\) 各加一，这很好实现。\(a\) 能直接到 \(A\) 中任意点的充要条件是 \(w(a,A) = sz_A-1\)（\(sz_A\) 是 \(A\) 代表的点双连通分量的大小）。

必胜条件可以转化为：对于一个根为 \(x\) 的子树中，所有 \(u\) 是圆点，\(v\) 是方点，\(dep_u<dep_v\) 的边 \((u,v)\) （如下图红边）均合法。记不合法的边的数量为 \(f_x\)，满足条件且不合法的的边称为不合法边。

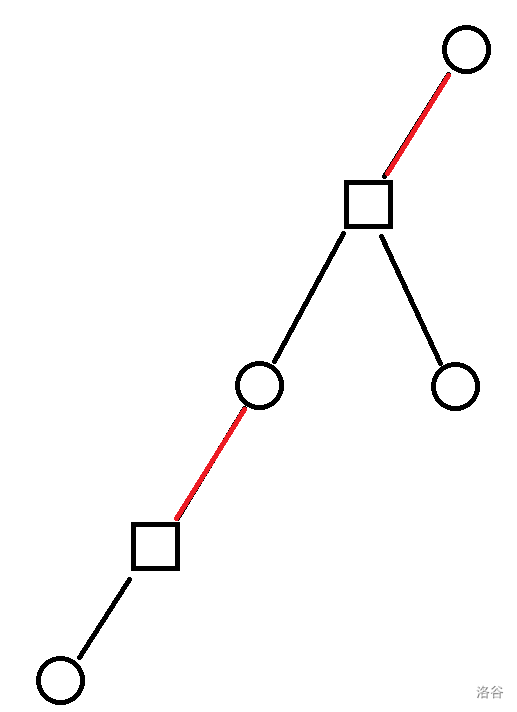
容易得到转移：\(f_{y \in son_x} \rightarrow f_x\)。对于不合法边 \((u,v)\)，为代码更好写，让 \(f_v \leftarrow f_v+1\)。

考虑换根 dp，记 \(g_x\) 为删去 \(x\) 的子树（除了 \(x\)）剩下的子树中不合法边的数量。

转移为：\(g_y=g_x+f_x-f_y+\Delta\)。

\(\Delta\) 的取值有：

• \((x,y)\) 有原来是不合法边，\(\Delta=-1\)。
• \((x,y)\) 现在是不合法边，\(\Delta=1\)。
• \((x,y)\) 啥都不是，\(\Delta=0\)。

最后用 lca 求出需要满足的子树 \(x\)，注意特判情况（2）。

默认 \(n,m,q\) 同级，时间复杂度为 \(O(n\log n)\)。

update on 2024.10.3 修改代码中的部分错误

Code:

#include<iostream>
#include<cstdlib>
#include<ctime>
#include<cassert>
#include<vector>
#include<cmath>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
using namespace std;
const int N = 2e5 + 10, M = 2 * N;
int dfn[N], low[N], st[N], sz[N], f[N], g[N], tot;
int fa[N][21], dep[N], n, m, q, ifa[N];
vector <int> e[N];
int head[N], vi[M], ne[M], wi[M], htot;
vector < pair <int, int> > vt;
void addedge(int u, int v){
	ne[++htot] = head[u], vi[htot] = v, head[u] = htot;
}
void add(int u, int v){
	addedge(u, v);
	addedge(v, u);
}
void tarjin(int x){
	dfn[x] = low[x] = ++dfn[0], st[++st[0]] = x;
	for(int y : e[x]){
		if(!dfn[y]){
			tarjin(y);
			low[x] = min(low[x], low[y]);
			if(low[y] == dfn[x]){
				add(x, ++tot);
				sz[tot] = 2;
				while(st[st[0]] != y){
					sz[tot]++;
					add(st[st[0]--], tot);
				}
				add(st[st[0]--], tot);
			}
		}
		else
			low[x] = min(low[x], dfn[y]);
	}
}
void ad(int u, int v){
	while(u != v){
		if(dep[u] < dep[v])
			swap(u, v);
		wi[ifa[u]]++, u = fa[u][0];
	}
}
void dfs1(int x, int pfa){
	dep[x] = dep[pfa] + 1, fa[x][0] = pfa;
	for(int i = 1; i <= 20; i++)
		fa[x][i] = fa[fa[x][i - 1]][i - 1];
	for(int i = head[x]; i; i = ne[i]){
		int y = vi[i];
		if(y == pfa)
			continue;
		ifa[y] = i;
		dfs1(y, x);
	}
}
void dfs2(int x, int pfa, int op){
	f[x] = op;
	for(int i = head[x]; i; i = ne[i]){
		int y = vi[i];
		if(y == pfa)
			continue;
		dfs2(y, x, (x <= n && wi[i] != sz[y] - 1));
		f[x] += f[y];
	}
}
void dfs3(int x, int pfa){
	for(int i = head[x]; i; i = ne[i]){
		int y = vi[i];
		if(y == pfa)
			continue;
		int t = g[x] + f[x] - f[y];
		if(y <= n && wi[i] != sz[x] - 1)
			t++;
		if(x <= n && wi[i] != sz[y] - 1)
			t--;
		g[y] = t;
		dfs3(y, x);
	}
}
int lca(int x, int y){
	if(dep[x] < dep[y])
		swap(x, y);
	for(int i = 20; ~i; i--)
		if(dep[fa[x][i]] >= dep[y])
			x = fa[x][i];
	if(x == y)
		return x;
	for(int i = 20; ~i; i--)
		if(fa[x][i] != fa[y][i])
			x = fa[x][i], y = fa[y][i];
	return fa[x][0];
}
bool check(int x, int y){
	if(lca(x, y) == x){
		int z = y;
		for(int i = 20; ~i; i--)
			if(dep[fa[z][i]] > dep[x])
				z = fa[z][i];
		return f[z] == 0;
	}
	return g[x] == 0;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> n >> m >> q;
	for(int i = 1, u, v; i <= m; i++){
		cin >> u >> v;
		vt.push_back(make_pair(u, v));
		e[u].push_back(v);
		e[v].push_back(u);
	}
	tot = n;
	tarjin(1);
	dfs1(1, 0);
	for(auto i : vt)
		ad(i.first, i.second);
	dfs2(1, 0, 0);
	dfs3(1, 0);
	bool flag = 0;
	for(int i = 1; i <= n; i++)
		flag |= (f[i] + g[i] == 0);
	while(q--){
		int a, b;
		cin >> a >> b;
		if(flag){
			cout << "Yes\n";
			continue;
		}
		cout << (check(a, b)? "Yes\n" : "No\n");
	}
}