低秩稀疏矩阵恢复|ADM(IALM)算法
一曲新词酒一杯,去年天气旧亭台。夕阳西下几时回?
无可奈何花落去,似曾相识燕归来。小园香径独徘徊。
———《浣溪沙·一曲新词酒一杯》——晏殊
更多精彩内容请关注微信公众号 “优化与算法”
上一期介绍了低秩矩阵填充问题,这一期介绍一下低秩稀疏矩阵恢复问题。
1. 低秩矩阵恢复
将一个矩阵 \(\bf{D}~(\bf {D} = \bf {A_0} +\bf E_0)\) 分解为一个低秩矩阵部分 \(\bf{A}\) 和一个独立同分布的高斯矩阵 \(\bf{E}\) 的问题是经典的主成分分析(PCA)问题,可以通过对矩阵 \(\bf{D}\) 进行奇异值分解得到最优解。
然而,当矩阵 \(\bf{E_0}\) 为稀疏的噪声矩阵时,PCA不再适用于解决这个问题。此时 ,将一个矩阵 \(\bf{D}~(\bf {D} = \bf {A_0} +\bf E)\) 分解为一个低秩矩阵部分 \(\bf{A}\) 和一个稀疏矩阵部分 \(\bf{E}\) 的问题可以建模为下述优化问题:
其中 \({\bf{D}},{\bf{A}},{\bf{E}},{{\bf{A}}_0},{{\bf{E}}_0}{ \in \mathbb{R}^{m \times n}}\),\(\bf D\) 是观测矩阵。(1)式中 \(rank(\bf A)\) 和 \({\left\| {\bf{E}} \right\|_0}\) 都是非线性且非凸的,优化起来非常困难,这个问题也被称为主成分追踪(Principal component pursuit, PCP)。幸运的是我们提前知道一些先验信息,即矩阵 \(\bf A\) 是低秩的且矩阵 \(\bf E\) 是稀疏的,从上一期介绍的关于矩阵填充理论中可知,矩阵的秩和 \(\ell_0\) 范数问题都可以进行凸松弛,从而为求解上述问题提供了途径。由于矩阵的核范数是矩阵秩的凸包络,矩阵的(1,1)范数是矩阵0范数的凸包络,因此可以将问题(1)松弛为如下凸优化问题:
求解式(2)也称为鲁棒主成分分析(RPCA)。
文献[1]中指出,只要低秩矩阵 \(\bf{A_0}\) 的奇异值分布合理且稀疏矩阵的非零元素均匀分布,那么凸优化问题PCP就能够以接近1的概率从未知的任意误差中恢复出原始低秩矩阵 \(\bf A_0\) 来。
求解(2)式的算法可以分为如下几大类:
- 迭代阈值算法
对于PCP问题时,迭代阈值算法(Iterative Thresholding, IT) 通过交替更新矩阵 \(\bf A\) 和 \(\bf E\) 来求解。IT算法的迭代形式简单且收敛,但它的收敛速度比较慢,且难以选取合适的步长。因此,IT算法具有有限的应用范围。 - 加速近端梯度算法
加速近端梯度算法(Accelerated Proximal Gradient, APG)的主要思想是利用了Nesterov加速,使算法能够快速收敛。 - 对偶方法
将原问题转化为其对偶问题(非线性、非光滑),并使用最速上升法等可以求解。对偶方法比APG算法具有更好的可扩展性,这是因为在每次迭代过程中对偶方法不需要矩阵的完全奇异值分解。 - 增广拉格朗日乘子法
这些方法都非常经典,这里不再细述,总的来说,只要将问题转化为凸问题,就有一大堆方法可以用来求解。这里仅介绍一种增广拉格朗日乘子算法,即交替方向方法(Alternating direction methods, ADM),也称为不精确拉格朗日乘子法(Inexact ALM, IALM)。
下面给出上述几种算法的比较(数据来源于网络)
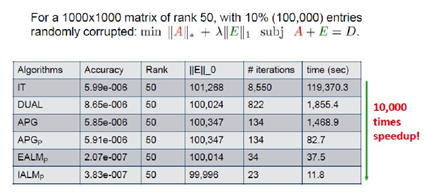
2. 交替方向算法(ADM)
对于优化问题(2),首先构造增广拉格朗日函数:
当 \({\bf{Y}} = {{\bf{Y}}_k},u = {u_k}\) 时,使用交替方法求解块优化问题:
使用精确拉格朗日乘子法(Exact ALM, EALM)交替迭代矩阵 \(\bf A\) 和 \(\bf E\),直到满足终止条件为止。若 \({\bf{E}} = {\bf{E}}_{k + 1}^j\),则
再根据 \({\bf{A}}_{k + 1}^{j + 1}\) 更新矩阵 \(\bf E\):
记 \({\bf{A}}_{k + 1}^{\rm{*}}\) 和 \({\bf{E}}_{k + 1}^{\rm{*}}\) 分别为 \({\bf{A}}_{k + 1}^{j + 1}\) 和 \({\bf{E}}_{k + 1}^{j + 1}\) 的精确值,则矩阵 \(\bf Y\) 的更新公式为:
参数 \({u_k}\) 可以更新如下:
其中 \(\rho>1\) 为常数,\(\varepsilon>0\) 为一个小的正数。
上述精确ALM方法在内循环中要多次更新,进行多次奇异值分解,为此文献[1]提出了非精确拉格朗日乘子法(Inecact ALM, IALM),它不需要在每次外循环开始之前要求 \(\mathop {\min }\limits_{{\bf{A}},{\bf{E}}} L({\bf{A}},{\bf{E}},{{\bf{Y}}_k},{u_k})\) 的精确解,也就是去掉了ALM方法的内循环,其更新公式变成了如下形式:
上面式子中的奇异值阈值算子 \({D_{\frac{1}{{{u_k}}}}}( \cdot )\) 和软阈值算子 \({S_{\frac{\lambda }{{{u_k}}}}}( \cdot )\) 的定义参见上一期<低秩矩阵填充|奇异值阈值算法>。
4. 低秩矩阵恢复的应用
低秩矩阵恢复技术是一个非常有研究价值和实用价值的技术,它的应用也非常广泛,比如说:
-
视频背景建模。
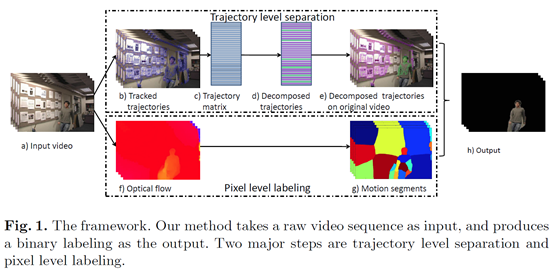
-
图像恢复(去光照、阴影等)

-
图像类别标签净化
-
文本主题分析
-
音乐词曲分离
-
图像矫正与去噪
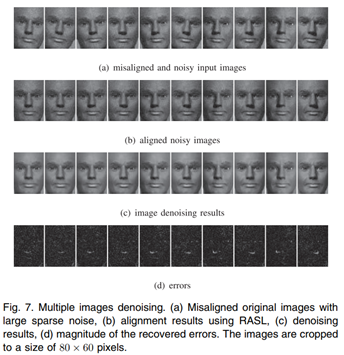
-
图像对齐
5. 仿真
ADM算法matlab代码如下:
function [L,S] = pcp_ad(M,u,lambda,itemax,tol)
% solve PCP problem by ADM algorithm
% v1.0 2020-1-1
% function:solve the following optimization problem
% min ||X||*+lambda||E||_F
% s.t. M = A+E
% initialize S0 and Y0 and L0
[m,n] = size(M) ;
S = zeros(m,n) ;
Y = S ;
L = S ;
% the observed matrix can contain non number
unobserved = isnan(M);
M(unobserved) = 0;
if nargin < 2
lambda = 1 / sqrt(max(m,n));
end
if nargin < 3
u = 10*lambda;
end
if nargin < 4
tol = 1e-6;
end
if nargin < 5
itemax = 1000;
end
for ii = 1:itemax
L = sig_thre(M-S+(1/u)*Y,(1/u)) ;
S = soft_thre(M-L+(1/u)*Y, lambda/u) ;
Z = M-L-S ;
Y = Y+u*Z ;
error = norm(M-L-S,'fro')/norm(M,'fro') ;
if (ii == 1) || (mod(ii, 10) == 0) || (error < tol)
fprintf(1, 'iter: %04d\terr: %f\trank(L): %d\tcard(S): %d\n', ...
ii, error, rank(L), nnz(S));
end
if error<tol
break;
end
end
数值测试代码:
% solve PCP problem by alternating direction method
clear
clc
m = 100 ;
n = 100 ;
r = 0.05*n ;
rate = 0.05 ;
% Generating a low rank matrix
LL = randn(m,r)/sqrt(m)*randn(r,n)/sqrt(n) ;
% Generating a large sparse noise matrix (Bernoulli matrix)
SS = randi([0,1],m,n) ;
SS(SS==0) = -1 ;
% sampling
ss = SS(:) ;
index = sort(randperm(m*n,ceil(rate*n*m))) ;
ss1 = zeros(m*n,1) ;
ss1(index) = ss(index) ;
SS = reshape(ss1,m,n) ;
M = LL+SS ;
lambda = 1/sqrt(max(m,n)) ;
u = 10*lambda ;
% [L,S] = pcp_ad(M,u,lambda,1000) ;
[L,S] = RobustPCA(M,lambda,u);
% [L,S] = pcp_ad(M,u,lambda,500,1e-8);
% [L,S] = adm_lrr(M);
MM = M-L-S ;
norm(M-MM,'fro')/norm(M,'fro')
norm(M-L-S,'fro')/norm(M,'fro')
norm(L-LL,'fro')/norm(LL,'fro')
norm(S-SS,'fro')/norm(SS,'fro')
function A = soft_thre(B,T)
A = sign(B).*max(abs(B)-T,0) ;
end
function [A] = sig_thre(B,T)
[s,v,d] = svd(B,'econ') ;
% v(v<T) = 0 ;
% A = s*v*d' ;
A = s*soft_thre(v,T)*d' ;
end
运行上面程序,显示结果norm(M-L-S,'fro')/norm(M,'fro')约为9e-7,norm(L-LL,'fro')/norm(LL,'fro')约为1e-5。
低秩图像恢复仿真程序:
% low rank and sparse noise image recovery
clear
clc
A = imread('C:\xxx\xxx\xxx.bmp') ;
WW = double(A) ;
a1 = double(A(:,:,1)) ;
a2 = double(A(:,:,2)) ;
a3 = double(A(:,:,3)) ;
[M,N] = size(a1);
X = zeros(M,N,3);
for jj = 1:3
lambda = 1*1 / sqrt(max(M,N));
u = 1*lambda;
[ X(:,:,jj),S(:,:,jj)] = RobustPCA(WW(:,:,jj),lambda,u,1e-8,200) ;
end
figure(1)
subplot(3,1,1)
imshow(A)
title("原图",'fontsize',12)
subplot(3,1,2)
imshow(uint8(X))
title("低秩图",'fontsize',12)
d = S ;
d(d<20) = 255 ;
subplot(3,1,3)
imshow(uint8(d))
title("噪声图",'fontsize',12)
低秩图像恢复结果如下:





从上面图像恢复结果来看,效果还不错。
参考文献
[1] Candès, E. J., Li, X., Ma, Y., & Wright, J. (2011). Robust principal component analysis?. Journal of the ACM (JACM), 58(3), 11.
[2] 史加荣, 郑秀云, 魏宗田, & 杨威. (2013). 低秩矩阵恢复算法综述. 计算机应用研究, 30(6), 1601-1605.
[3] Cui, X., Huang, J., Zhang, S., & Metaxas, D. N. (2012, October). Background subtraction using low rank and group sparsity constraints. In European Conference on Computer Vision (pp. 612-625). Springer, Berlin, Heidelberg.
[4] Wright, J., Ganesh, A., Rao, S., Peng, Y., & Ma, Y. (2009). Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Advances in neural information processing systems (pp. 2080-2088).
[5] Peng, Y., Ganesh, A., Wright, J., Xu, W., & Ma, Y. (2012). RASL: Robust alignment by sparse and low-rank decomposition for linearly correlated images. IEEE transactions on pattern analysis and machine intelligence, 34(11), 2233-2246.
更多精彩内容请关注订阅号优化与算法

更多精彩内容请关注微信公众号 “优化与算法”


