题意:给定一个竞赛图,且其中不包含任意一组三元环 $(a, b, c)$,满足 $a \to d$,$b \to d$,$c \to d$,求每个点两两之间的距离之和(若无法达到即为 $614n$)。
数据范围:$n \leq 8e3$。
首先竞赛图相当于是一个边都有向的完全图,其名称由来就是有一堆人竞赛,打一场单循环制比赛,胜者向负者连边这种。
由于这个是一个竞赛图,首先考虑缩点,那么可以得出一个强联通分量中的点也是一个竞赛图(因为一个强联通分量是一个导出子图)。
手玩几个例子,可以发现缩完点后的图也是一个竞赛图(除去重边自环),因为原图中一个强联通分量中的点对于这个强联通分量之外的点的边的方向是固定的(否则就会产生一个新的大的强联通分量),且由原图可知两两之间都有连边。
对于一个有环的竞赛图,显然是不能够将每个点进行排序的,那么一个无环的竞赛图呢?
答案是肯定的。
考虑先证明一个 $\text{DAG}$ 中一定有一个入度为 $0$ 的点。
考虑反证法,假设这个 $\text{DAG}$ 中每个点都一定会有一个前驱节点 $pre$,那么从任意一个点的 $pre$ 出发,不断去找 $pre$,最终一定会形成一个环(类似 $ρ$ 的一个环,这里就是 $ρ$ 型证明),证毕。
那么对于图中的一个入度为 $0$ 的点,显然它无法被任何人战胜,那么这个点即可定为 $\text{rank}$ $1$,然后再删掉这个点,剩下的图仍然是一个满足 $\text{DAG}$ 性质的竞赛图,以此类推,可以将每个点排序。
另一种证明方法就是对于 $a \to b$,$b \to c$,因为原图中没有环且是一个竞赛图,因此一定能够导出 $a \to c$,所以这个是一个全序关系,那么这整个图就一定能够给每个点排序了。
而又由于这是一个竞赛图,因此它画出来大概长这样:
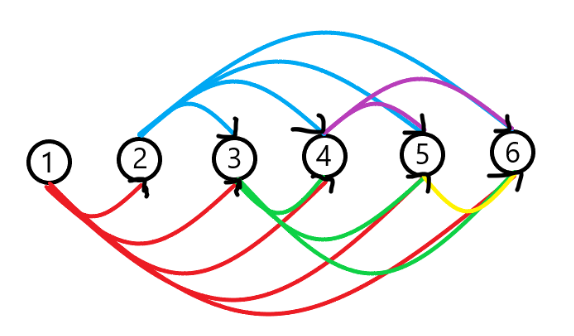
我们再来看一下这个橙框里的点缩点前的特征。
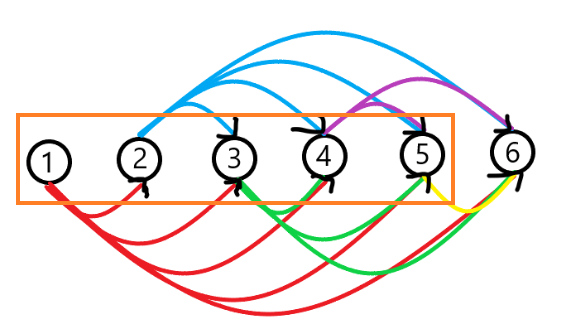
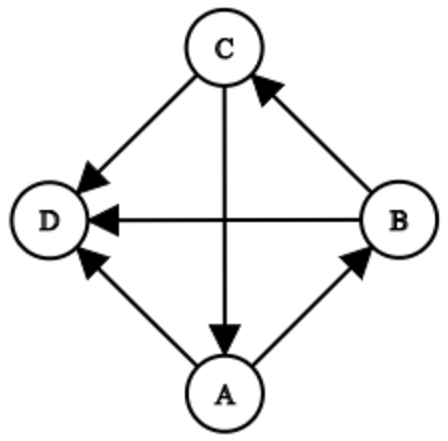
这时我们就要看看原题中的那个竞赛图的限制条件了,即不存在上面的那种三元环。
考虑到橙框里的点中,每个点都会向后面的点连一条边,那么就可以推出橙框里的点在原图中不存在三元环。
那么这橙框中的每一个点在原图中就有下面三个限制条件:
- 竞赛图;
- 强联通;
- 没有三元环;
但是手玩几个例子发现并不存在这样的图,或者说发现只有在缩完的点在原图中只是一个点的时候才能满足这种情况。
考虑证明。
对于一个点的图,显然它满足条件。
对于一个两个点的图,它并不满足强联通的这个条件。
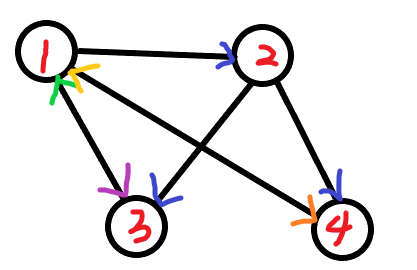
对于一个三个点的图:$点 1 \to 点 2$,$点 2 \to 点 3$ 的边是可以随便的,但是此时 $点 1 \to 点 3$ 的边就没有办法连了,若选择绿色的,必然不满足没有三元环,若选择紫色,必然不满足强联通。
对于一个四个点的图:那么前面三个点的图只能选择紫色的边,而加入 $点 4$ 的时候,同样会面对要么不满足没有三元环,要么不满足强联通的情况。
以此类推,除了一个点,必然没有这样的图。
那么就能够得出橙色框里的点在原图中都是单点了,因此可以先得出一部分答案(设总点数为 $n$,橙框中有 $m$ 个点),即为:
$\frac{m \times (m - 1)}{2} \times (1 + 614n)$ $+$ $m \times (n - m) \times (1 + 614n)$。
那么剩下要求的答案即为橙框之外的点内部的两两距离之和。
由于它是一个竞赛图,直觉告诉我们这个图里两两之间的距离不会太大,因此可以尝试分类讨论。
先考虑这个图中两点之间的最大距离是多少。
首先若距离为 $1$,显然是可以的;
若距离为 $2$,可以构造出一个三元环,所以是可以的;
若距离为 $3$,那么考虑右边这个图: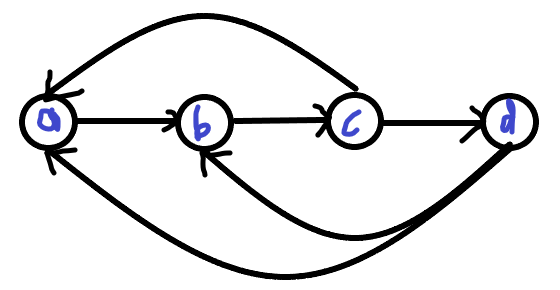
它是满足的。
若距离为 $4$,那么考虑右边这个图: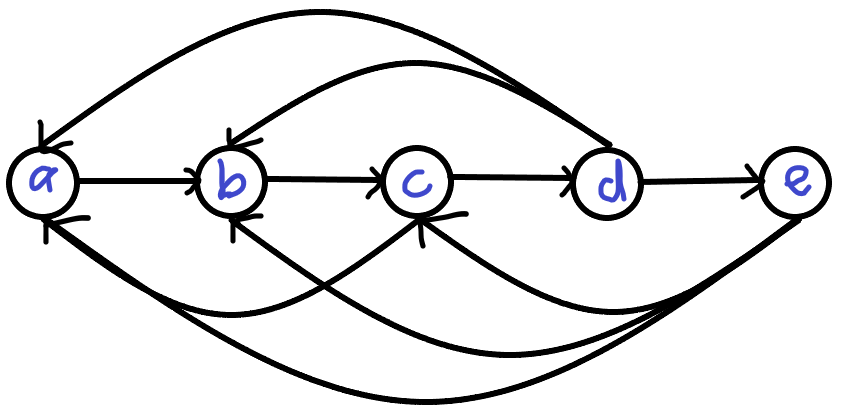
此时不难发现 $(c, d, e)$ 这个三元环同时连向了 $a$ 点,因此就不满足题目中的条件了。
所以距离最大只能为 $3$。
所以分三种情况讨论,设 $c1$ 为长度为 $1$ 的最短路,$c2$ 为长度为 $2$ 的最短路,$c3$ 为长度为 $3$ 的最短路。
那么 $c1$ 的值就为这个图中的边数,即 $c1 = \frac{(n - m) \times (n - m - 1)}{2}$。
再来考虑图中 $c2$ 的数量(而 $c3$ 的数量就为 $\frac{(n - m) \times (n - m - 1)}{2} - \text{num}(c2)$)。
首先长度为 $2$ 的最短路径必然不能存在一条长度为 $1$ 的路径,并且还须恰好经过一个点(两条边),如下图:
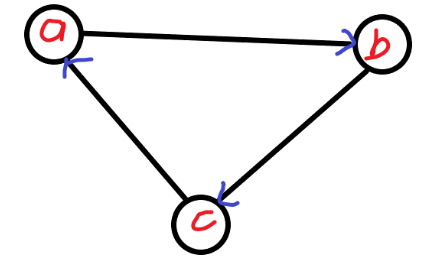
但是如果直接枚举三个点的话复杂度为 $\mathcal{O}(n^3)$,$n$ $=$ $8e3$ 过不去。
因此我们考虑找到 $c$ 点的性质,或者是找到一个特殊的 $c$ 点。
因为这个 $c$ 点只是一个普通的点,因此它并没有什么特殊的性质,所以考虑找到一个特殊的 $c$ 点。
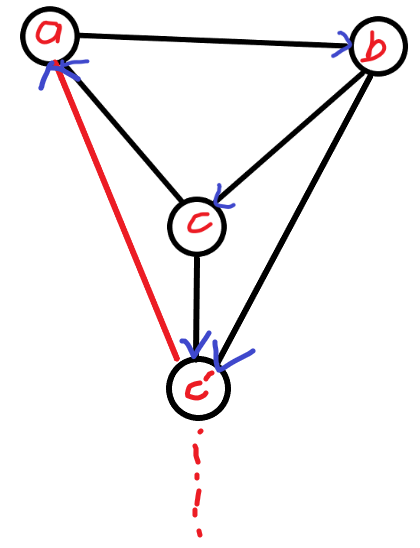
看上图中的 $c’$ 点,根据题目中给定的条件,若存在 $b \to c$,$b \to c'$,$c \to a$,$a \to b$,$c \to c'$,一定能够推出 $c' \to a$(否则就不满足题目中不存在那个子图的条件)。
假设我们把 $c \to a$,$a \to b$ 称作 $C(a)$,把 $b$ 的所有出点称作 $N^{+}(b)$。
那么对于 $c \in N^{+}(b)$,$c' \in N^{+}(b)$,且 $c \to c'$,那么若有 $c$ 满足 $C(a)$,$c'$ 也一定满足 $C(a)$ 。
那么这些满足条件的 $c$ 中哪个是最特殊的呢?是最下面的那个。
最下面的那个点满足一个条件,就是所有它上面点若满足 $C(a)$,那么它也一定能够满足 $C(a)$,所以如果它不满足 $C(a)$ 了,就不会再有点满足 $C(a)$ 了,因此我们计算一个点是否满足就可以得到所有点,所以说它是特殊的。
但是由于这是一张竞赛图,每个点间都有连边,所以最下面的那个点不一定就是出度为 $0$ 的点(因为可能没有出度为 $0$ 的点)。
但仔细想想就能发现即使下面没有出度为 $0$ 的点,但是一定会在下面形成一个环(一个强联通分量),而这个强联通分量中的点都满足上面说的那个特殊性。
所以就可以将 $N^{+}(b)$ 进行缩点,再 $\text{toposort}$ 一下,找到拓扑序最后的那个点,随便拎出来一个判断一下是否满足条件即可。
但有没有发现一丝丝不对劲儿,那就是 $\text{Tarjan}$ 的复杂度是 $\mathcal{O}(n + m)$ 的,拓扑排序也会遍历到所有的边也是 $\mathcal{O}(m)$ 的,而竞赛图中总时间复杂度 $\mathcal{O}(n \times m)$ 肯定会炸掉,考虑优化。
对于原图中的任意一个导出子图,它都满足原图的两个性质,一个是竞赛图,另一个是不存在原题中的那种三元环。
同理可证,对于由 $N^{+}(b)$ 中的所有点及其有关的边构成的导出子图中,其模样一定是:

其中橙框中的点都是单点,最后一个点是一个强连通分量。
我们发现其实我们只需要找到最后一个强连通分量中的任意一个点,并且只能用 $\mathcal{O}(n)$ 的复杂度。
观察一下发现,所有不是我们需要求的那些单点,都能只通过一条边到达我们要求的点。
所以考虑枚举这些点,并记录一个 $res$ 值表示最终找到的我们要求的点。
每次判断一下当前的 $res$ 能够到达枚举到的这个点,如果能的话就更新 $res$ 值。
根据上面观察到的性质,可以证明如果枚举到我们要求的点时一定会更新答案,并且由于那个强连通分量出度为 $0$,因此答案不会再更新出这个强连通分量。
时间复杂度:$\mathcal{O}(n^2)$
code :Submission #169030675 - Codeforces


 posted on
posted on

