「洛谷P1402」酒店之王 解题报告
P1402 酒店之王
题目描述
XX酒店的老板想成为酒店之王,本着这种希望,第一步要将酒店变得人性化。由于很多来住店的旅客有自己喜好的房间色调、阳光等,也有自己所爱的菜,但是该酒店只有p间房间,一天只有固定的q道不同的菜。
有一天来了n个客人,每个客人说出了自己喜欢哪些房间,喜欢哪道菜。但是很不幸,可能做不到让所有顾客满意(满意的条件是住进喜欢的房间,吃到喜欢的菜)。
这里要怎么分配,能使最多顾客满意呢?
输入输出格式
输入格式:
第一行给出三个正整数表示n,p,q(<=100)。
之后n行,每行p个数包含0或1,第i个数表示喜不喜欢第i个房间(1表示喜欢,0表示不喜欢)。
之后n行,每行q个数,表示喜不喜欢第i道菜。
输出格式:
最大的顾客满意数。
输入输出样例
输入样例#1:
2 2 2
1 0
1 0
1 1
1 1
输出样例#1:
1
算法
网络最大流。这里不详细讲,请大家先掌握。
思路
注意,以下出现的所有边边权皆为1,且其反向边边权为0
我们以房间、菜、人为点建图。
像这样:
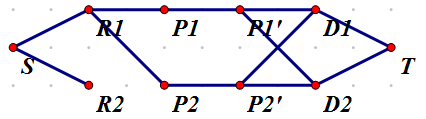
S(=0)表示额外建的一个起始点,Ri(=i + n + n)表示第i个房间,Di(=i+n+n+p)表示第i种菜,由于人只有一个,而网络流处理只经过一个点不方便,我们采用一种神奇方法——拆点!也就是说,把一个人看做两个点,要匹配这个人必须经过这个人两点之间的边,这样就可以控制这个人只匹配一次。如图,Pi(=i)、Pi'(=i+n)表示第i个人。
然后建边。如图,将S与所有Ri相连,将所有的Di与T相连,S作为源点,T作为汇点。如果Pi喜欢Rj,就将Pi与Rj相连。如果Pi喜欢Dj,就将Dj与Pi'之间相连。当然,Pi与Pi'之间也要连一条边。
然后就可以套网络最大流辣。最后得出的答案即为满意数。
拓展
有一天来了n批客人,每批客人喜欢的菜、房间都相同。第i批客人有gi位客人。其余同原题。
HINT:我们可以把每批客人当做2个点Pi、Pi',
在Pi、Pi'之间连gi条边连一条权为gi的边即可。菜、房间每种有多个同理。
代码
#include<bits/stdc++.h>
using namespace std;
#define open(s) freopen( s".in", "r", stdin ), freopen( s".out", "w", stdout )
#define MAXN 405
#define MAXM 40005
int n, p, q;
int hd[MAXN], nxt[MAXM << 1], to[MAXM << 1], val[MAXM << 1], tot(1);
int ans, dis[MAXN];
queue<int> Q;
int x, y;
int S, T;
void Add( int x, int y, int z ){ nxt[++tot] = hd[x]; hd[x] = tot; to[tot] = y; val[tot] = z; }
bool BFS(){
while( !Q.empty() ) Q.pop();
memset( dis, 0, sizeof dis );
Q.push(S); dis[S] = 1;
while( !Q.empty() ){
x = Q.front(); Q.pop();
for ( int i = hd[x]; i; i = nxt[i] )
if ( val[i] && !dis[to[i]] ){
dis[to[i]] = dis[x] + 1;
Q.push( to[i] );
if ( to[i] == T ) return 1;
}
}
return 0;
}
int DFS( int x, int fl ){
if ( x == T ) return fl;
int res(fl), k;
for ( int i = hd[x]; i && res; i = nxt[i] ){
if ( val[i] && dis[to[i]] == dis[x] + 1 ){
k = DFS( to[i], min( res, val[i] ) );
if ( !k ) dis[to[i]] = 0;
val[i] -= k; val[i^1] += k; res -= k;
}
}
return fl - res;
}
int main(){
scanf( "%d%d%d", &n, &p, &q );
S = 0; T = 1 + n + n + p + q;
for ( int i = 1; i <= n; ++i ) Add( i, i + n, 1 ), Add( i + n, i, 0 );
for ( int i = 1; i <= p; ++i ) Add( S, i + n + n, 1 ), Add( i + n + n, S, 0 );
for ( int i = 1; i <= q; ++i ) Add( i + n + n + p, T, 1 ), Add( T, i + n + n + p, 0 );
for ( int i = 1; i <= n; ++i )
for ( int j = 1; j <= p; ++j ){
int t; scanf( "%d", &t );
if ( t ) Add( j + n + n, i, 1 ), Add( i, j + n + n, 0 );
}
for ( int i = 1; i <= n; ++i )
for ( int j = 1; j <= q; ++j ){
int t; scanf( "%d", &t );
if ( t ) Add( i + n, j + n + n + p, 1 ), Add( j + n + n + p, i + n, 0 );
}
int t;
while( BFS() )
while( ( t = DFS( S, 0x7f7f7f7f ) ) > 0 ) ans += t;
printf( "%d\n", ans );
return 0;
}
总结
这类题目如果要用网络最大流解决,一般来说,将“选择者”放中间,并且要拆点,“被选物”放两边,直接与源点、汇点相连。但是这种做法“被选物”不能多于两种。
如果多于两种,要怎么做呢? 我也不知道 QAQ)求教大佬QAQ


