「BZOJ1722」「Usaco2006 Mar」Milk Team Select产奶比赛 解题报告
Milk Team Select 产奶比赛
Description
Farmer John’s N (\(1 \le N \le 500\)) cows are trying to select the milking team for the world-famous Multistate Milking Match-up (MMM) competition. As you probably know, any team that produces at least X (\(1 \le X \le 1,000,000\)) gallons of milk is a winner. Each cow has the potential of contributing between \(-10,000\) and \(10,000\) gallons of milk. (Sadly, some cows have a tendency to knock over jugs containing milk produced by other cows.) The MMM prides itself on promoting family values. FJ’s cows have no doubt that they can produce X gallons of milk and win the contest, but to support the contest’s spirit, they want to send a team with as many parent-child relationships as possible (while still producing at least X gallons of milk). Not surprisingly, all the cows on FJ’s farm are female. Given the family tree of FJ’s cows and the amount of milk that each would contribute, compute the maximum number of parent-child relationships that can exist in a winning team. Note that a set of cows with a grandmother-mother-daughter combination has two parent-child relationships (grandmother-mother, mother-daughter).
约翰的N(\(1 \le N \le 500\))头奶牛打算组队去参加一个世界级的产奶比赛(Multistate Milking Match-up,缩写为MMM).她们很清楚其他队的实力,也就是说,她们派出的队只要能产出至少X(\(1 \le X \le 1000000\))加仑牛奶,就能赢得这场比赛. 每头牛都能为集体贡献一定量的牛奶,数值在\(-10000\)到\(10000\)之间(有些奶牛总是想弄翻装着其他奶牛产的奶的瓶子).
MMM的举办目的之一,是通过竞赛中的合作来增进家庭成员之间的默契.奶牛们认为她们总是能赢得这场比赛,但为了表示对比赛精神的支持,她们希望在选出的队伍里能有尽可能多的牛来自同一个家庭,也就是说,有尽可能多对的牛有直系血缘关系(当然,这支队伍必须能产出至少X加仑牛奶).当然了,所有的奶牛都是女性,所以队伍里所有直系血亲都是母女关系. 约翰熟知所有奶牛之间的血缘关系.现在他想知道,如果在保证一支队伍能赢得比赛的情况下,队伍中最多能存在多少对血缘关系.注意,如果一支队伍由某头奶牛和她的母亲、她的外祖母组成,那这支队伍里一共有2对血缘关系(这头奶牛外祖母与她的母亲,以及她与她的母亲).
Input
Line 1: Two space-separated integers, N and X.
Lines 2..N+1: Line i+1 contains two space-separated integers describing cow i. The first integer is the number of gallons of milk cow i would contribute. The second integer (range 1..N) is the index of the cow’s mother. If the cow’s mother is unknown, the second number is 0. The family information has no cycles: no cow is her own mother, grandmother, etc.
第1行:两个用空格隔开的整数N和X.
第2到N+1行:每行包括两个用空格隔开的整数,第一个数为一只奶牛能贡献出的牛奶的加仑数,第二个数表示她的母亲的编号.如果她的母亲不在整个牛群里,那第二个数为0.并且,血缘信息不会出现循环,也就是说一头奶牛不会是自己的母亲或祖母,或者更高代的祖先.
Output
Line 1: The maximum number of parent-child relationships possible on a winning team. Print -1 if no team can win.
输出在一个能获胜的队伍中,最多可能存在的有血缘关系的牛的对数.如果任何一支队伍都不可能获胜,输出-1.
Sample Input
5 8
-1 0
3 1
5 1
-3 3
2 0
第一个数字代表这头奶的产量,第二个数字代表其父亲点是哪一个.
INPUT DETAILS: There are 5 cows. Cow 1 can produce -1 gallons and has two daughters, cow 2 and 3, who can produce 3 and 5 gallons, respectively. Cow 3 has a daughter (cow 4) who can produce -3 gallons. Then there’s cow 5, who can produce 2 gallons.
Sample Output
2
HINT
约翰一共有5头奶牛.第1头奶牛能提供-1加仑的牛奶,且她是第2、第3头奶牛的母亲.第2、第3头奶牛的产奶量务别为3加仑和5加仑.第4头奶牛是第3头奶牛的女儿,她能提供-3加仑牛奶.还有与其他牛都没有关系的第5头奶牛,她的产奶量是2加仑.
最好的一支队伍包括第1,2,3,5头奶牛.她们一共能产出\(-1+3+5+2=9 \ge 8\)加仑牛奶,并且这支队伍里有2对牛有血缘关系(1-2和1-3).如果只选第2,3,5头奶牛,虽然总产奶量会更高(10加仑),但这支队伍里包含的血缘关系的对数比上一种组合少(队伍里没有血缘关系对).
Source
思路
很明显,这是一道动态规划题(看着很像背包嘛)那我们要用什么作为下表呢?
- 以牛奶量:牛奶量的数据范围较大,最多只能开一维数组(除非你开滚动数组)。总体来说较难考虑。
- 以关系数:关系数最多只有 N - 1 对,可以给每头牛开一个 MAXN 的数组,看起来更行得通。。。
还有,因为要考虑关系数的转换问题,所以还有开一维[0/1]表示这头牛取不取。
我们发现,这些关系是无环的,或者说这是一个森林(本来我想用拓扑排序,后来还是放弃了。。。),所以可以再建立一头“牛祖先”,连接原来所有祖先,构成一棵树(即无母亲的节点都认0为母亲)。
对于样例,可以构成如图的一棵树:
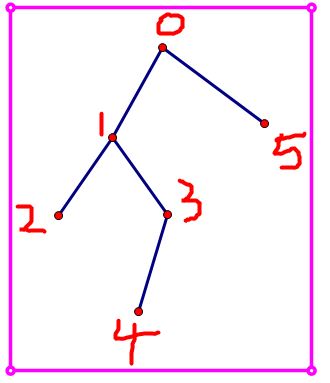
整理一下,刚才讲到建立一个 \(int f[MAXN][MAXN][2];\) 的数组,\(f[i][j][op]\)表示以第 i 个节点为根的树 共有 j 对关系,op = 1 时表示取这个节点,op = 0 时表示不取。
可以把 关系数 作为背包容量,牛奶量 作为 价值
用分组背包的方法来考虑。
具体的部分自己慢慢理解吧。
上代码——
代码
#include<cstdio>
#include<iostream>
using namespace std;
#define MAXN 505
#define INF 0x3f3f3f3f
int N, X, ans;
int c[MAXN], t;
int head[MAXN], to[MAXN << 1], nxt[MAXN << 1], tot(0);
int f[MAXN][MAXN][2];
void Add( int x, int y ){
to[++tot] = y; nxt[tot] = head[x]; head[x] = tot;
}
void DFS( int x, int fa ){
for ( int i = 1; i <= N; i++ ) f[x][i][0] = f[x][i][1] = -INF;//初始值均为负无穷
for ( int i = head[x]; i; i = nxt[i] ){
if ( to[i] == fa ) continue;
DFS( to[i], x );//先完成子节点
for ( int j = N; j >= 0; --j ){//分配的关系数
for ( int k = 0; k <= j; ++k ){//背包——
f[x][j][1] = max( f[x][j][1], f[x][j - k][1] + max( k == 0 ? -INF : f[to[i]][k - 1][1], f[to[i]][k][0] ) );
f[x][j][0] = max( f[x][j][0], f[x][j - k][0] + max( f[to[i]][k][1], f[to[i]][k][0] ) );
}
}
}
for ( int i = 0; i <= N; ++i ) f[x][i][1] += c[x];//若取这个节点,加上这个点的价值
}
int main(){
scanf( "%d%d", &N, &X );
for ( int i = 1; i <= N; ++i ){
scanf( "%d%d", &c[i], &t );
Add( i, t ); Add( t, i );//链式前向星存边
}
DFS( 0, -1 );
int ans(N);
while( ans >= 0 ){
if ( f[0][ans][0] >= X ) break;
ans--;
}
printf( "%d\n", ans );
return 0;
}

