常用排序算法小结

　　算法一直是编程的基础，而排序算法是学习算法的开始，排序也是数据处理的重要内容。所谓排序是指将一个无序列整理成按非递减顺序排列的有序序列。排列的方法有很多，根据待排序序列的规模以及对数据的处理的要求，可以采用不同的排序方法。那么就整理下网上搜索的资料，按自己的理解，把C语言的8大排序算法列出来。

本文将简单小结一下常见的排序算法

排序的分类：内排序和外排序。
内排序:指在排序期间数据对象全部存放在内存的排序。
外排序:指在排序期间全部对象个数太多,不能同时存放在内存,必须根据排序过程的要求,不断在内、外存之间移动的排序。
内排序的方法有许多种,按所用策略不同,可归纳为五类:插入排序、选择排序、交换排序、归并排序、分配排序和计数排序。
插入排序主要包括直接插入排序，折半插入排序和希尔排序两种;
选择排序主要包括直接选择排序和堆排序;
交换排序主要包括冒泡排序和快速排序;
归并排序主要包括二路归并(常用的归并排序)和自然归并。
分配排序主要包括箱排序和基数排序。
计数排序就一种。

稳定排序:假设在待排序的文件中,存在两个或两个以上的记录具有相同的关键字,在用某种排序法排序后,若这些相同关键字的元素的相对次序仍然不变,则这种排序方法是稳定的。
其中冒泡,插入,基数,归并属于稳定排序;选择,快速,希尔,堆属于不稳定排序。

一.交换类排序法

所谓交换排序法是指借助数据元素之间互相交换进行排序的方法。冒泡排序与快速排序法都属于交换类排序方法。

1、冒泡排序（BubbleSort）

冒泡排序的基本概念：

依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。至此第一趟结束，将最大的数放到了最后。在第二趟：仍从第一对数开始比较（因为可能由于第2个数和第3个数的交换，使得第1个数不再小于第2个数），将小数放前，大数放后，一直比较到倒数第二个数（倒数第一的位置上已经是最大的），第二趟结束，在倒数第二的位置上得到一个新的最大数（其实在整个数列中是第二大的数）。如此下去，重复以上过程，直至最终完成排序。由于在排序过程中总是小数往前放，大数往后放，相当于气泡往上升，所以称作冒泡排序。

实现：

外循环变量设为i，内循环变量设为j。假如有10个数需要进行排序，则外循环重复9次，内循环依次重复9，8，...，1次。每次进行比较的两个元素都是与内循环j有关的，它们可以分别用a[j]和a[j+1]标识，i的值依次为1,2,...,9，对于每一个i,j的值依次为1,2,...10-i。

图示：

C语言实现：

  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 
  4 //bubble sort 1:move the largest to the last
  5 void maopao1(int *num,int len)
  6 {
  7     int i,j;
  8     int temp;
  9     for (i = 0; i < len-1; ++i)
 10     {
 11         for (j = i+1; j<len; ++j)
 12         {
 13             if (num[i]>num[j])
 14             {
 15                 temp=num[i];
 16                 num[i]=num[j];
 17                 num[j]=temp;
 18             }
 19         }
 20     }
 21 }
 22 
 23 //bubble sort 2:move the smallest to the foremost
 24 void maopao2(int *num,int len)
 25 {
 26     int i,j;
 27     int temp;
 28     for (i = 0; i < len; i++)
 29     {
 30         for (j = len-1; j>i; j--)
 31         {
 32             if (num[j-1]>num[j])
 33             {
 34                 temp=num[j-1];
 35                 num[j-1]=num[j];
 36                 num[j]=temp;
 37             }
 38         }
 39     }
 40 }
 41 
 42 
 43 //the basic bubble sort
 44 void maopao3(int *num,int len)
 45 {
 46     int i,j;
 47     int temp;
 48     for (i = 0; i < len; ++i)
 49     {
 50         for (j = 0; j<len-i; ++j)
 51         {
 52             if (num[j]>num[j+1])
 53             {
 54                 temp=num[j+1];
 55                 num[j+1]=num[j];
 56                 num[j]=temp;
 57             }
 58         }
 59     }
 60 }
 61 
 62 
 63 //bubble sort improvement:set the a flag to reduce the times for comprision
 64 void maopao4(int *num,int len)
 65 {
 66     int i,j;
 67     int temp;
 68     int flag;
 69     for (i = 0; i < len&&flag; i++)
 70     {
 71         flag=0;
 72         for (j = len-1; j>i; j--)
 73         {
 74             if (num[j-1]>num[j])
 75             {    
 76                 temp=num[j-1];
 77                 num[j-1]=num[j];
 78                 num[j]=temp;
 79                 flag=1;
 80             }
 81         }
 82     }
 83 }
 84 
 85 int main(int argc, char const *argv[])
 86 {
 87     int i;
 88     int num[9]={2,8,4,3,0,1,7,9,5};
 89     int length=sizeof(num)/sizeof(int);
 90     printf("Before sort:\n");
 91     for (i = 0; i < length; ++i)
 92     {
 93         printf("%d\t",num[i]);
 94     }
 95     printf("\n");
 96 
 97     maopao1(num,length);
 98     //maopao2(num,length);
 99     //maopao3(num,length);
100     //maopao4(num,length);
101 
102     printf("After sort:\n");
103     for (i = 0; i < length; ++i)
104     {
105         printf("%d\t",num[i]);
106     }
107     printf("\n");
108 
109     return 0;
110 }

BubbleSort

性能分析：

　　若记录序列的初始状态为"正序"，则冒泡排序过程只需进行一趟排序，在排序过程中只需进行n-1次比较，且不移动记录；反之，若记录序列的初始状态为"逆序"，则需进行n(n-1）/2次比较和记录移动。因此冒泡排序总的时间复杂度为O(n*n)。

2、快速排序（Quicksort）

基本思想：

　　快速排序是对冒泡排序的一种改进。由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

实现：

　　设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用第一个数据）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

一趟快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

2）以第一个数组元素作为关键数据，赋值给key，即 key=A[0]；

3）从j开始向前搜索，即由后开始向前搜索（j -- ），找到第一个小于key的值A[j]，A[i]与A[j]交换；

4）从i开始向后搜索，即由前开始向后搜索（i ++ ），找到第一个大于key的A[i]，A[i]与A[j]交换；

5）重复第3、4、5步，直到 I=J； (3,4步是在程序中没找到时候j=j-1，i=i+1，直至找到为止。找到并交换的时候i， j指针位置不变。另外当i=j这过程一定正好是i+或j-完成的最后令循环结束。）

图示：

举例说明：

如无序数组[6 2 4 1 5 9]

a),先把第一项[6]取出来,

用[6]依次与其余项进行比较,

如果比[6]小就放[6]前边,2 4 1 5都比[6]小,所以全部放到[6]前边

如果比[6]大就放[6]后边,9比[6]大,放到[6]后边,//6出列后大喝一声,比我小的站前边,比我大的站后边,行动吧!霸气十足~

一趟排完后变成下边这样:

排序前 6 2 4 1 5 9

排序后 2 4 1 5 6 9

b),对前半拉[2 4 1 5]继续进行快速排序

重复步骤a)后变成下边这样:

排序前 2 4 1 5

排序后 1 2 4 5

前半拉排序完成,总的排序也完成:

排序前:[6 2 4 1 5 9]

排序后:[1 2 4 5 6 9]

C语言实现：

 1 #include <stdio.h>
 2 
 3 
 4 void swap(int *num,int a,int b)
 5 {
 6     int temp;
 7     temp=num[a];
 8     num[a]=num[b];
 9     num[b]=temp;
10 }
11 
12 
13 
14 int Partition(int*num, int low, int high)
15 {
16     int pivotkey=num[low];
17     while(low<high)
18     {
19         while(low<high&&pivotkey<=num[high])
20         {
21             high--;
22         }
23         swap(num,low,high);
24 
25         while(low<high&&pivotkey>=num[low])
26         {
27             low++;
28         }
29         swap(num,low,high);
30     }
31 
32     return low;  //return the position of the pivotkey
33 }
34 
35 void QuickSort(int *num,int low,int high)
36 {
37     int pivotkey;
38     if (low<high)
39     {
40         pivotkey=Partition(num,low,high);
41         QuickSort(num,low,pivotkey-1);
42         QuickSort(num,pivotkey+1,high);
43     }
44 }
45 
46 
47 int main(int argc, char const *argv[])
48 {  
49     int i;
50     int num[10]={2,8,4,3,0,1,7,6,9,5};
51     int length=sizeof(num)/sizeof(int);
52    
53     printf("Before quick sort:\n");
54     for (i = 0; i < length; ++i)
55     {
56         printf("%d\t",num[i]);
57     }
58     printf("\n\n");
59 
60     QuickSort(num,0,length-1);  
61 
62     printf("After quick sort:\n");
63     for (i = 0; i < length; ++i)
64     {
65         printf("%d\t",num[i]);
66     }
67     printf("\n");
68 
69     return 0;
70 }

QuickSort

性能分析

快速排序的时间主要耗费在划分操作上，对长度为k的区间进行划分，共需k-1次关键字的比较。

最坏情况是每次划分选取的基准都是当前无序区中关键字最小(或最大)的记录，划分的结果是基准左边的子区间为空(或右边的子区间为空)，而划分所得的另一个非空的子区间中记录数目，仅仅比划分前的无序区中记录个数减少一个。时间复杂度为O(n*n)

在最好情况下，每次划分所取的基准都是当前无序区的"中值"记录，划分的结果是基准的左、右两个无序子区间的长度大致相等。总的关键字比较次数：O(nlgn)

尽管快速排序的最坏时间为O(n²)，但就平均性能而言，它是基于关键字比较的内部排序算法中速度最快者，快速排序亦因此而得名。它的平均时间复杂度为O(nlgn)。

这里有一个视频比较形象地说明了这两个有趣的排序算法：http://www.tudou.com/programs/view/htKY1-Rj9ZE/?resourceId=0_06_02_99

二、插入类排序

　插入排序(Insertion Sort)的基本思想是：每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子文件中的适当位置，直到全部记录插入完成为止。

插入排序一般意义上有两种：直接插入排序和希尔排序，下面分别介绍。

3、直接插入排序

基本思想：

最基本的操作是将第i个记录插入到前面i-1个以排好序列的记录中。具体过程是：将第i个记录的关键字K依次与其前面的i-1个已经拍好序列的记录进行比较。将所有大于K的记录依次向后移动一个位置，直到遇到一个关键字小于或等于K的记录，此时它后面的位置必定为空，则将K插入。

图示：

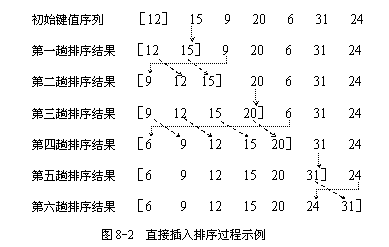
C语言实现：

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 void insert_sort(int *num,int len)
 5 {
 6     
 7     int i,j;
 8     int guard;
 9     for (i = 1; i < len; i++)
10     {
11         if (num[i]<num[i-1])
12         {
13             guard=num[i]; //set the number which is under insert as the current guard 
14             for (j = i-1;(j>=0)&&(num[j]>guard); j--)
15             {
16                 num[j+1]=num[j];//move the position one by one 
17             }
18             //num[j]>guard is true ,then end the for cricle,so the num[j] is the position to insert the guard
19             //num[j+1] is the approriate because j-- for break out the for cricle
20             num[j+1]=guard;//insert the under_insert number to the approriate position
21         }
22     }
23 
24 }
25 
26 int main(int argc, char const *argv[])
27 {
28     int i;
29     int num[9]={2,8,4,3,0,1,7,9,5};
30     int length=sizeof(num)/sizeof(int);
31     printf("Before sort:\n");
32     for (i = 0; i < length; ++i)
33     {
34         printf("%d\t",num[i]);
35     }
36     printf("\n\n");
37 
38     insert_sort(num,length);
39 
40     printf("After sort:\n");
41     for (i = 0; i < length; ++i)
42     {
43         printf("%d\t",num[i]);
44     }
45     printf("\n");
46 
47     return 0;
48 }

InsertSort

算法分析：

1．算法的时间性能分析
　对于具有n个记录的文件，要进行n-1趟排序。
各种状态下的时间复杂度：
初始文件状态正序反序无序(平均)
字比较次数 1 i+1 （i-2）/2
总关键字比较次数 n-1 (n+2)(n-1)/2 ≈n2/4
第i趟记录移动次数 0 i+2 （i-2）/2
总的记录移动次数 0 (n-1)(n+4)/2 ≈n2/4
时间复杂度 0（n） O（n2） O（n2）
注意：
　初始文件按关键字递增有序，简称"正序"。
　初始文件按关键字递减有序，简称"反序"。
2．算法的空间复杂度分析
　算法所需的辅助空间是一个监视哨，辅助空间复杂度S(n)=O(1)。是一个就地排序。
3．直接插入排序的稳定性
　直接插入排序是稳定的排序方法。

直接插入排序法，针对少量的数据项排序，速度比较快，数据越大，这中方法的劣势也就越明显了。

改进方案：折半插入排序（binary insertion sort）

思路：折半插入排序（binary insertion sort）是对插入排序算法的一种改进，由于排序算法过程中，就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列，这样我们不用按顺序依次寻找插入点，可以采用折半查找的方法来加快寻找插入点的速度。

具体操作：在将一个新元素插入已排好序的数组的过程中，寻找插入点时，将待插入区域的首元素设置为a[low],末元素设置为a[high]，则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素小，则选择a[low]到a[m-1]为新的插入区域(即high=m-1)，否则选择a[m+1]到a[high]为新的插入区域（即low=m+1），如此直至low<=high不成立，即将此位置之后所有元素后移一位，并将新元素插入a[high+1]。

C语言实现：

 1  void BInsertSort(int data[],int n)
 2   {
 3        int low,high,mid;
 4        int temp,i,j;
 5        for(i=1;i<n;i++)
 6        {
 7                        low=0;
 8                        temp=data[i];// 保存要插入的元素
 9                       high=i-1;
10                     while(low<=high) //折半查找到要插入的位置
11                     {                       
12                    mid=(low+high)/2;
13                       if(data[mid]>temp)
14                          high=mid-1;
15                       else
16                        low=mid+1;
17                      }
18                 int j = i;    
19             while ((j > low) && (arr[j - 1] > t))    
20             {    
21                 arr[j] = arr[j - 1];//交换顺序    
22                 --j;    
23             }    
24             arr[low] = temp;  
25 
26  } 
27 
28  }

BinaryInsertionSort

算法分析：折半插入排序算法是一种稳定的排序算法，比直接插入算法明显减少了关键字之间比较的次数，因此速度比直接插入排序算法快，但记录移动的次数没有变，所以折半插入排序算法的时间复杂度仍然为O(n^2)，与直接插入排序算法相同。附加空间O(1)。

4、希尔排序

希尔排序(Shell Sort)是插入排序的一种。是针对直接插入排序算法的改进。该方法又称缩小增量排序，因DL．Shell于1959年提出而得名。

基本思想：
　先取一个小于n的整数d₁作为第一个增量，把文件的全部记录分成d₁个组。所有距离为d_l的倍数的记录放在同一个组中。先在各组内进行直接插人排序；然后，取第二个增量d₂<d₁重复上述的分组和排序，直至所取的增量d_t=1(d_t<d_t-l<…<d₂<d₁)，即所有记录放在同一组中进行直接插入排序为止。
　该方法实质上是一种分组插入方法。

举例阐述：

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了，然后再以3为步长进行排序：

排序之后变为：

最后以1步长进行排序（此时就是简单的插入排序了）。

图示：

C语言实现：

 1 #include <stdio.h>
 2 
 3 
 4 
 5 void ShellSort(int *num,int len)
 6 {
 7     //the step means the memberof of each group
 8     //At first .the step is large,and decrease after each cricle
 9     int i,j,step,temp;
10     for (step =len/3; step>0; step-=2)//the rule o the step set is according to  your minds
11     {
12         for (i = step; i < len; ++i)
13         {
14             temp=num[i];
15             for (j = i-step;j>=0&&num[j]>temp;j-=step)
16             {    
17                  num[j+step]=num[j];
18             }
19             num[j+step]=temp;
20         }
21     }
22 }
23 
24 
25 
26 int main(int argc, char const *argv[])
27 {  
28     int i;
29     int num[10]={2,8,4,3,0,1,7,6,9,5};
30     int length=sizeof(num)/sizeof(int);
31    
32     printf("Before Shell sort:\n");
33     for (i = 0; i < length; ++i)
34     {
35         printf("%d\t",num[i]);
36     }
37     printf("\n\n");
38 
39     ShellSort(num,length);
40 
41     printf("After Shell sort:\n");
42     for (i = 0; i < length; ++i)
43     {
44         printf("%d\t",num[i]);
45     }
46     printf("\n");
47 
48     return 0;
49 }

ShellSort

性能分析：

　　希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

最差时间复杂度	根据步长序列的不同而不同。已知最好的: 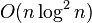$O(n\log^2 n)$
最优时间复杂度	O(n)
平均时间复杂度	根据步长序列的不同而不同。

4、归并排序

　　归并排序是把序列递归地分成短序列，递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列，不断合并直到原序列全部排好序。可以发现，在1个或2个元素时，1个元素不会交换，2个元素如果大小相等也没有人故意交换，这不会破坏稳定性。那么，在短的有序序列合并的过程中，稳定是是否受到破坏？没有，合并过程中我们可以保证如果两个当前元素相等时，我们把处在前面的序列的元素保存在结果序列的前面，这样就保证了稳定性。所以，归并排序也是稳定的排序算法。

C语言实现：（递归实现方式）

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 void Merge(int *num,int low,int mid,int high)  
 5 {  
 6     //将两个有序的子文件R[low..m)和R[m+1..high]归并成一个有序的子文件R[low..high]  
 7     int i=low,j=mid+1,k=0;                //置初始值 
 8     int *new_num;                        //R1是局部向量  
 9     new_num=(int *)malloc((high-low+1)*sizeof(int));  
10     if(!new_num)  
11     {  
12         return;                         //申请空间失败  
13     }  
14   
15     while((i<=mid)&&(j<=high))                //两子文件非空时取其小者输出到R1[k]上  
16     {  
17         new_num[k++]=(num[i]<=num[j])?num[i++]:num[j++];  
18     }  
19  
20     while(i<=mid)                         //若第1个子文件非空，则复制剩余记录到R1中  
21     {  
22         new_num[k++]=num[i++];  
23     }  
24 
25     while(j<=high)                      //若第2个子文件非空，则复制剩余记录到R1中  
26     {  
27         new_num[k++]=num[j++];  
28     }  
29   
30     for(k=0,i=low;i<=high;k++,i++)  
31     {  
32         num[i]=new_num[k];                     //归并完成后将结果复制回R[low..high]  
33     }  
34 }  
35   
36 void MergeSort(int *num,int low,int high)  
37 {     
38     //用分治法对R[low..high]进行二路归并排序  
39     int mid;  
40 
41     if(low<high)  
42     {   //区间长度大于1   
43         mid=(low+high)/2;                 //分解  
44 
45         MergeSort(num,low,mid);           //递归地对R[low..mid]排序  
46         MergeSort(num,mid+1,high);        //递归地对R[mid+1..high]排序  
47 
48         Merge(num,low,mid,high);          //组合，将两个有序区归并为一个有序区  
49     }  
50 }  
51 
52 int main(int argc, char const *argv[])
53 {  
54     int i;
55     int num[9]={2,8,4,3,0,1,7,9,5};
56     int length=sizeof(num)/sizeof(int);
57    
58     printf("Before merge sort:\n");
59     for (i = 0; i < length; ++i)
60     {
61         printf("%d\t",num[i]);
62     }
63     printf("\n\n");
64 
65     MergeSort(num,0,length-1);  
66 
67     printf("After merge sort:\n");
68     for (i = 0; i < length; ++i)
69     {
70         printf("%d\t",num[i]);
71     }
72     printf("\n");
73 
74     return 0;
75 }

MergeSort

C语言实现：（非递归实现方式）

（待补充）

5、堆排序

（待补充）

排序算法复杂度：

按平均时间将排序分为四类：
（1）平方阶(O(n²))排序
    　一般称为简单排序，例如直接插入、直接选择和冒泡排序；
（2）线性对数阶(O(nlgn))排序
    　如快速、堆和归并排序；
（3）O(n^1+￡)阶排序
    　￡是介于0和1之间的常数，即0<￡<1，如希尔排序；
（4）线性阶(O(n))排序
    　如桶、箱和基数排序。

不同条件下，排序方法的选择
(1)若n较小(如n≤50)，可采用直接插入或直接选择排序。
    　当记录规模较小时，直接插入排序较好；否则因为直接选择移动的记录数少于直接插人，应选直接选择排序为宜。
(2)若文件初始状态基本有序(指正序)，则应选用直接插人、冒泡或随机的快速排序为宜；
(3)若n较大，则应采用时间复杂度为O(nlgn)的排序方法：快速排序、堆排序或归并排序。
    　快速排序是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
    　堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
    　若要求排序稳定，则可选用归并排序。但本章介绍的从单个记录起进行两两归并的排序算法并不值得提倡，通常可以将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子文件，然后再两两归并之。因为直接插入排序是稳定的，所以改进后的归并排序仍是稳定的。

4)在基于比较的排序方法中，每次比较两个关键字的大小之后，仅仅出现两种可能的转移，因此可以用一棵二叉树来描述比较判定过程。
    　当文件的n个关键字随机分布时，任何借助于"比较"的排序算法，至少需要O(nlgn)的时间。
    　箱排序和基数排序只需一步就会引起m种可能的转移，即把一个记录装入m个箱子之一，因此在一般情况下，箱排序和基数排序可能在O(n)时间内完成对n个记录的排序。但是，箱排序和基数排序只适用于像字符串和整数这类有明显结构特征的关键字，而当关键字的取值范围属于某个无穷集合(例如实数型关键字)时，无法使用箱排序和基数排序，这时只有借助于"比较"的方法来排序。
    　若n很大，记录的关键字位数较少且可以分解时，采用基数排序较好。虽然桶排序对关键字的结构无要求，但它也只有在关键字是随机分布时才能使平均时间达到线性阶，否则为平方阶。同时要注意，箱、桶、基数这三种分配排序均假定了关键字若为数字时，则其值均是非负的，否则将其映射到箱(桶)号时，又要增加相应的时间。
(5)有的语言(如Fortran，Cobol或Basic等)没有提供指针及递归，导致实现归并、快速(它们用递归实现较简单)和基数(使用了指针)等排序算法变得复杂。此时可考虑用其它排序。
(6)本章给出的排序算法，输人数据均是存储在一个向量中。当记录的规模较大时，为避免耗费大量的时间去移动记录，可以用链表作为存储结构。譬如插入排序、归并排序、基数排序都易于在链表上实现，使之减少记录的移动次数。但有的排序方法，如快速排序和堆排序，在链表上却难于实现，在这种情况下，可以提取关键字建立索引表，然后对索引表进行排序。然而更为简单的方法是：引人一个整型向量t作为辅助表，排序前令t[i]=i(0≤i<n)，若排序算法中要求交换R[i]和R[j]，则只需交换t[i]和t[j]即可；排序结束后，向量t就指示了记录之间的顺序关系：
        R[t[0]].key≤R[t[1]].key≤…≤R[t[n-1]].key
若要求最终结果是：
       R[0].key≤R[1].key≤…≤R[n-1].key
则可以在排序结束后，再按辅助表所规定的次序重排各记录，完成这种重排的时间是O(n)。

posted @ 2015-07-17 21:05 GeekerLou 阅读(277) 评论(0) 编辑收藏举报

刷新页面返回顶部

常用排序算法小结

公告