import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense, LSTM
import math
import numpy as np
import matplotlib.pyplot as plt
import datetime
# 加载数据集
def parser(x):
return datetime.datetime.strptime(x, '%Y/%m/%d')
# 将时间序列转换为监督类型的数据序列
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = pd.DataFrame(data)
cols, names = [], []
# 这个for循环是用来输入列标题的var1(t-1),var1(t),var1(t+1),var1(t+2)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# 转换为监督型数据的预测序列，每四个一组，对应var1(t-1),var1(t),var1(t+1),var1(t+2)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, 1)) for j in range(n_vars)]
# 拼接数据
agg = pd.concat(cols, axis=1)
agg.columns = names
# 将null值转换为0
if dropnan:
agg.dropna(inplace=True)
print(agg)
return agg
# 对传入的数列作差分操作，相邻两只相间
def difference(dataset, interval=1):
diff = []
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i-interval]
diff.append(value)
return pd.Series(diff)
# 将序列转换为用于监督学习的训练和测试集
def prepare_data(series, n_test, n_lag, n_seq):
# 提取原始值
raw_values = series.values
# 将数据转换为静态的
diff_series = difference(raw_values, 1)
diff_values = diff_series.values
diff_values = diff_values.reshape(len(diff_values), 1)
# 重新调整数据为（-1， 1）之间
scaler = MinMaxScaler(feature_range=(-1, 1))
scaled_values = scaler.fit_transform(diff_values)
scaled_values = scaled_values.reshape(len(scaled_values), 1)
# 转换为有监督的数据X,y
supervised = series_to_supervised(scaled_values, n_lag, n_seq)
supervised_values = supervised.values
# 分割为测试数据和训练数据
train, test = supervised_values[:-n_test], supervised_values[-n_test:]
return scaler, train, test
# 匹配LSTM网络训练数据
def fit_lstm(train, n_lag, n_seq, n_batch, nb_epoch, n_neurons):
# 重塑训练数据格式[samples, timesteps, features]
X, y = train[:, :n_lag], train[:, n_lag:]
X = X.reshape(X.shape[0], 1, X.shape[1])
# 配置一个LSTM神经网络，添加网络参数
model = Sequential()
# 使 RNN 具有状态意味着每批样品的状态将被重新用作下一批样品的初始状态。
# 要在 RNN 中使用状态，你需要:
"""
通过将 batch_size 参数传递给模型的第一层来显式指定你正在使用的批大小。例如，对于 10 个时间步长的 32 样本的 batch，每个时间步长具有 16 个特征，batch_size = 32。
在 RNN 层中设置 stateful = True。
在调用 fit() 时指定 shuffle = False
重置累积状态：
使用 model.reset_states()来重置模型中所有层的状态
使用layer.reset_states()来重置指定有状态 RNN 层的状态
将一个很长的序列（例如时间序列）分成小序列来构建我的输入矩阵。那LSTM网络会发现我这些小序列之间的关联依赖吗？
不会，除非你使用 stateful LSTM 。大多数问题使用stateless LSTM即可解决，所以如果你想使用stateful LSTM，请确保自己是真的需要它。在stateless时，长期记忆网络并不意味着你的LSTM将记住之前batch的内容。
在Keras中stateless LSTM中的stateless指的是?
注意，此文所说的stateful是指的在Keras中特有的，是batch之间的记忆cell状态传递。而非说的是LSTM论文模型中表示那些记忆门，遗忘门，c，h等等在同一sequence中不同timesteps时间步之间的状态传递。
假定我们的输入X是一个三维矩阵，shape = （nb_samples, timesteps, input_dim），每一个row代表一个sample，每个sample都是一个sequence小序列。X[i]表示输入矩阵中第i个sample。步长啥的我们先不用管。
当我们在默认状态stateless下，Keras会在训练每个sequence小序列（=sample）开始时，将LSTM网络中的记忆状态参数reset初始化（指的是c，h而并非权重w），即调用model.reset_states()。
为啥stateless LSTM每次训练都要初始化记忆参数?
因为Keras在训练时会默认地shuffle samples，所以导致sequence之间的依赖性消失，sample和sample之间就没有时序关系，顺序被打乱，这时记忆参数在batch、小序列之间进行传递就没意义了，所以Keras要把记忆参数初始化。
那stateful LSTM到底怎么传递记忆参数？
首先要明确一点，LSTM作为有记忆的网络，它的有记忆指的是在一个sequence中，记忆在不同的timesteps中传播。举个例子，就是你有一篇文章X，分解，然后把每个句子作为一个sample训练对象（sequence），X[i]就代表一句话，而一句话里的每个word各自代表一个timestep时间步，LSTM的有记忆即指的是在一句话里，X[i][0]第一个单词（时间步）的信息可以被记忆，传递到第5个单词（时间步）X[i][5]中。
而我们突然觉得，这还远远不够，因为句子和句子之间没有任何的记忆啊，假设文章一共1000句话，我们想预测出第1001句是什么，不想丢弃前1000句里的一些时序性特征（stateless时这1000句训练时会被打乱，时序性特征丢失）。那么，stateful LSTM就可以做到。
在stateful = True 时，我们要在fit中手动使得shuffle = False。随后，在X[i]（表示输入矩阵中第i个sample）这个小序列训练完之后，Keras会将将训练完的记忆参数传递给X[i+bs]（表示第i+bs个sample）,作为其初始的记忆参数。bs = batch_size。这样一来，我们的记忆参数就能顺利地在sample和sample之间传递，X[i+n*bs]也能知道X[i]的信息。
stateful LSTM中为何一定要提供batch_size参数？
我们可以发现，记忆参数（state）是在每个batch对应的位置跳跃着传播的，所以batch_size参数至关重要，在stateful lstm层中必须提供。
那stateful时，对权重参数w有影响吗？
我们上面所说的一切记忆参数都是LSTM模型的特有记忆c，h参数，和权重参数w没有任何关系。无论是stateful还是stateless，都是在模型接受一个batch后，计算每个sequence的输出，然后平均它们的梯度，反向传播更新所有的各种参数。
如果你还是不理解，没关系，简单的说：
stateful LSTM：能让模型学习到你输入的samples之间的时序特征，适合一些长序列的预测，哪个sample在前，那个sample在后对模型是有影响的。
stateless LSTM：输入samples后，默认就会shuffle，可以说是每个sample独立，之间无前后关系，适合输入一些没有关系的样本。
如果你还是不理解，没关系……举个例子：
stateful LSTM：我想根据一篇1000句的文章预测第1001句，每一句是一个sample。我会选用stateful，因为这文章里的1000句是有前后关联的，是有时序的特征的，我不想丢弃这个特征。利用这个时序性能让第一句的特征传递到我们预测的第1001句。（batch_size = 10时）
stateless LSTM：我想训练LSTM自动写诗句，我想训练1000首诗，每一首是一个sample，我会选用stateless LSTM，因为这1000首诗是独立的，不存在关联，哪怕打乱它们的顺序，对于模型训练来说也没区别。
"""
model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))
model.add(Dense(y.shape[1]))
model.compile(loss='mean_squared_error', optimizer='adam')
print(model.summary())
# 调用网络，迭代数据对神经网络进行训练，最后输出训练好的网络模型
for i in range(nb_epoch):
model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
model.reset_states()
return model
# 用LSTM作预测
def forecast_lstm(model, X, n_batch):
# 重构输入参数[samples, timestemps, features]
X = X.reshape(1, 1, len(X))
# 开始预测
forecast = model.predict(X, batch_size=n_batch)
# 结果转换为数组
return [x for x in forecast[0, :]]
# 利用训练好的网络模型，对测试数据进行预测
def make_forecasts(model, n_batch, train, test, n_lag, n_seq):
forecasts = []
# 预测方式是用一个X值预测出后三步的Y值
for i in range(len(test)):
X, y = test[i, :n_lag], test[i, n_lag:]
# 调用训练好的模型预测未来数据
forecast = forecast_lstm(model, X, n_batch)
# 将预测的数据保存
forecasts.append(forecast)
return forecasts
# 对预测后的缩放值(-1,1)进行逆变换
def inverse_difference(last_ob, forecast):
# invert first forecast
inverted = []
inverted.append(forecast[0] + last_ob)
# propagate difference forecast using inverted first value
for i in range(1, len(forecast)):
inverted.append(forecast[i] + inverted[i-1])
return inverted
# 对预测数据进行逆变换
def inverse_transoform(series, forecasts, scaler, n_test):
inverted = []
for i in range(len(forecasts)):
# create array from forecast
forecast = np.array(forecasts[i])
forecast = forecast.reshape(1, len(forecast))
# 将预测后的数据缩放逆变换
inv_scale = scaler.inverse_transform(forecast)
inv_scale = inv_scale[0, :]
# invert differencing
index = len(series) - n_test + i - 1
last_ob = series.values[index]
# 将预测后的数据差值逆转换
inv_diff = inverse_difference(last_ob, inv_scale)
# 保存数据
inverted.append(inv_diff)
return inverted
# 评估每个预测时间步的RMSE
def evaluate_forecasts(test, forecasts, n_lag, n_seq):
for i in range(n_seq):
actual = [row[i] for row in test]
predicted = [forecast[i] for forecast in forecasts]
rmse = math.sqrt(mean_squared_error(actual, predicted))
print('t+%d RMSE: %f' % ((i+1), rmse))
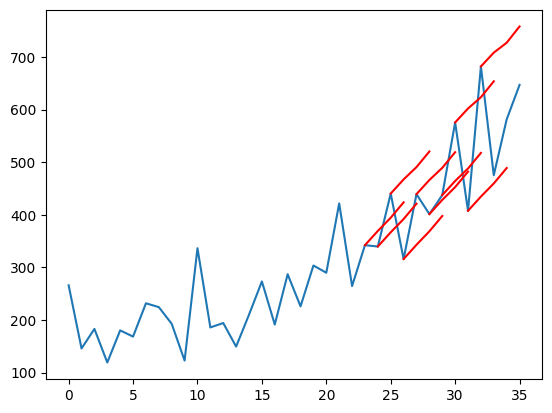
# 在原始数据集的上下文中绘制预测图
def plot_forecasts(series, forecasts, n_test):
# plot the entire datasets in blue
plt.plot(series.values)
# plot the forecasts in red
for i in range(len(forecasts)):
off_s = len(series) - n_test + i - 1
off_e = off_s + len(forecasts[i]) + 1
xaxis = [x for x in range(off_s, off_e)]
yaxis = [series.values[off_s]] + forecasts[i]
plt.plot(xaxis, yaxis, color='red')
plt.show()
# 加载数据
series = pd.read_csv('../LSTM系列/Multi-Step LSTM预测2/data_set/shampoo-sales.csv',
header=0, parse_dates=[0], index_col=0, date_parser=parser).squeeze('index')['Sales']
# 配置网络信息
n_lag = 1
n_seq = 3
n_test = 10
n_epochs = 5
n_batch = 1
n_neurons = 1
# 准备数据
scaler, train, test = prepare_data(series, n_test, n_lag, n_seq)
# 准备预测模型
model = fit_lstm(train, n_lag, n_seq, n_batch, n_epochs, n_neurons)
# 开始预测
forecasts = make_forecasts(model, n_batch, train, test, n_lag, n_seq)
# 逆转换训练数据和预测数据
forecasts = inverse_transoform(series, forecasts, scaler, n_test+2)
# 逆转换测试数据
actual = [row[n_lag:] for row in test]
actual = inverse_transoform(series, actual, scaler, n_test+2)
# 比较预测数据和测试数据，计算损失
evaluate_forecasts(actual, forecasts, n_lag, n_seq)
# 画图
plot_forecasts(series, forecasts, n_test+2)
