10-训练深度神经网络
理论部分
训练DNN常见问题
- 梯度消失或梯度爆炸问题
- 对于如此大的网络，你可能没有足够的训练数据，或者做标签的成本太高
- 训练可能会非常慢
- 具有数百万个参数的模型会有严重过拟合训练集的风险
梯度消失与梯度爆炸问题
- 反向传播算法的工作原理是从输出层到输入层，并在此过程中传播误差梯度。一旦算法计算出成本函数相对于网络中每个参数的梯度，就可以使用这些梯度以梯度下降步骤来跟心每个参数
- 不幸的是，随着算法向下传播到较低层，梯度通常会越来越小。结果梯度下降更新使较低层的连接权重保持不变，训练不能收敛到一个良好的解，称其为梯度消失问题。在某些情况下，可能会出现相反的情况：梯度可能会越来越大，各层需要更新很大的权重，直到算法发散为止，这是梯度爆炸问题，它出现在递归神经网络中
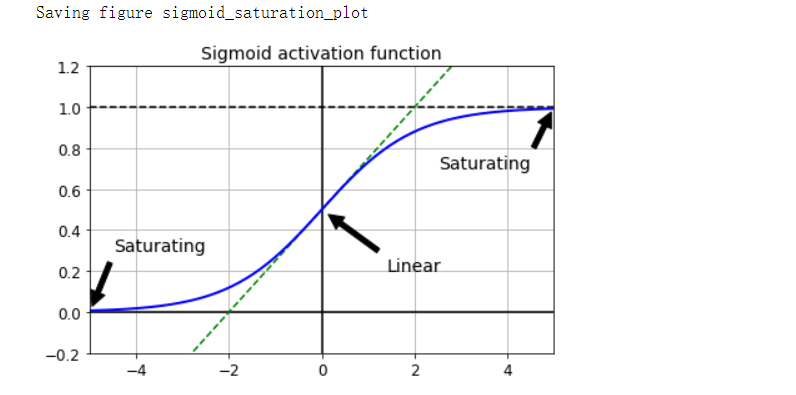
- 逻辑sigmoid激活函数和服从N(0,1)的权重初始化技术的问题
- 使用此激活函数和此初始化方案，每层输出的方差远大于其输入的方差
- 当输入变大(负数或正数)时，该函数会以0或1饱和，并且导数非常接近0。因此反向传播开始时它几乎没有梯度可以通过网络传播回去。当反向传播通过顶层向下传播时，存在的小梯度不断被稀释，因此对于底层来说，实际上什么也没有留下
解决梯度问题
-
Glorot和He初始化
- 为了缓解梯度不稳定，我们需要信号在两个方向上正确流动：进行预测时，信号为正向；在反向传播梯度时，信号为反向。我们既不希望信号消失，也不希望它爆炸并饱和。为了使信号正确流动，我们需要每层输出的方差等于其输入的方差，并且我们需要在反方向时流过某层之前和之后的梯度具有相同的方差
\[除非该层具有相等数量的输入和神经元，否则实际上不可能同时保证两者，但按照下述公式\\ 随机初始化每层的连接权重，可以实现一个很好的折中效果，称为Glorot初始化：\\ 正态分布，其均值为0，方差为\sigma^2=\frac{1}{fan_{avg}}，其中fan_{avg}=\frac{fan_{in}+fan_{out}}{2}\\ 或-r和+r之间的俊宇分布，其中r=\sqrt{\frac{3}{fan_avg}} \]-
LeCun初始化
\[如果用fan_{in}替换上述公式的fan_{avg}，则会得到LeCun初始化，当fan_{in}=fan_{out}时，\\ LeCun初始化等效于Glorot初始化 \] -
使用Glorot初始化可以大大加快训练速度
-
ReLU激活函数的初始化策略(及其变体，包括ELU激活函数)有时简称He初始化。而SELU激活函数它应该与LeCun初始化一起使用
初始化 激活函数 σ2(正常) Glorot None、tanh、logistic、softmax 1/fanavg He ReLU和变体 2/fanin LeCun SELU 1/fanin - 默认情况下，Keras使用具有均匀分布的Glorot初始化
-
非饱和激活函数
-
ReLU激活函数在深度神经网络中的表现非常好，主要是因为它对正值不饱和(并且计算速度很快)，但是ReLU激活函数并不完美，它有一个被称为“濒死的ReLU”的问题：在训练过程中，某些神经元实际上“死亡了”，这意味着它们停止输出除0以外的任何值，在某些情况下，你可能会发现网络中一半的神经元都死了，特别是如果你使用较大的学习率(ReLU函数的输入为负时，其梯度为0)
-
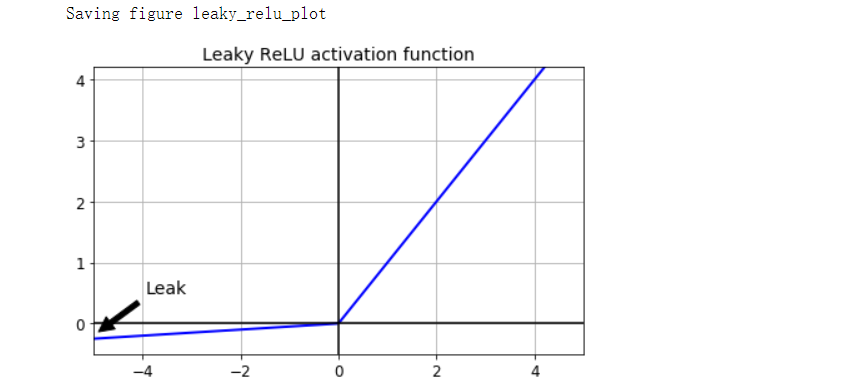
要解决此问题，需要使用ReLU函数的变体，例如leaky ReLU。该函数定义为LeakyReLUα(z)=max(αz, z)。超参数α定义函数“泄露”的程度：它是z<0时函数的斜率，通常设置为0.01，它们可能会陷入长时间的昏迷，但是有机会最后醒来。
-
其他观点
- 设置α=0.2(大泄露)似乎比α=0.01(小泄露)会产生更好的性能
- 随机的leaky ReLU(RReLU)
- 参数化的leaky ReLU(PReLU)，其中α可以在训练期间学习：PReLU在大型图像数据集上的性能明显由于ReLU，但是在较小的数据集上，它存在过拟合训练集的风险
-
ELU激活函数
\[ELU_\alpha(z)=\left\{\begin{matrix} \alpha(exp(z)-1)，如果z<0\\ z，如果z>=0 \end{matrix}\right . \]- ELU激活函数与ReLU函数非常相似，但有一些主要区别：
- 当z<0时，它取负值，这使该单元的平均输出接近于0，有助于缓解梯度消失的问题。
- 对于z<0，它具有非零梯度，从而避免了神经元死亡的问题
- 如果α等于1，则该函数在所有位置(包括z=0左右)都是平滑的，这有助于加速梯度下降，因为它在z=0的左右两侧弹跳不打
- ELU激活函数与ReLU函数非常相似，但有一些主要区别：
-
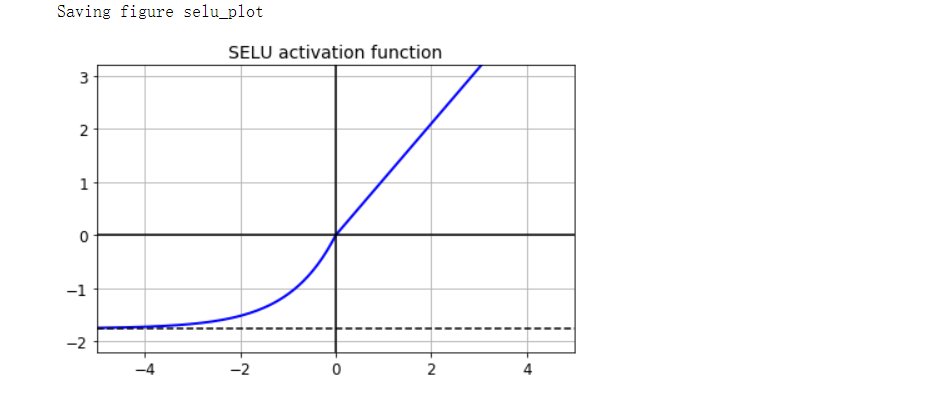
SELU激活函数
- SELU是可扩展的ELU，它是ELU激活函数的可扩展变体。如果你构建一个仅由密集层堆叠组成的神经网络，并且如果所有隐藏层都使用SELU激活函数，则该网络是自归一化的：每层的输出都倾向于在训练过程中保留平均值0和标准差1，从而解决了梯度消失/梯度爆炸的问题
- 产生自归一化的条件：
- 输入特征必须是标准化的(平均值为0，标准差为1)
- 每个隐藏层的权重必须使用LeCun正态初始化
- 网络的架构必须是顺序的
- 所有层都是密基层
-
如何选择神经网络隐藏层的激活函数
- 通常SELU>ELU>leaky ReLU(及其变体)>ReLU>tanh>logistic
- 如果网络的架构不能自归一化，那么ELU的性能可能会优于SELU(因为SELU在z=0时不平滑)
- 如果你非常关心运行时延迟，那么你可能更喜欢leaky ReLU
- 如果你有空闲时间和计算能力，则可以使用交叉验证来评估其他激活函数
- 如果网络过拟合，则为RReLU
- 如果你的训练集过大，则PReLU
- 如果你将速度放在首位，则ReLU可能仍然是最佳选择
-
-
批量归一化(BN)
- 该技术在模型中的每个隐藏层的激活函数之前或之后添加一个操作，该操作对每个输入零中心化并归一化，然后每层使用两个新的参数向量缩放和偏移其结果：一个用于缩放，另一个用于偏移。换句话说，该操作可以使模型学习各层输入的最佳缩放和均值。在许多情况下，如果你将BN层添加为神经网络的第一层，则无须归一化训练集，BN层会为你完成此操作
- 为了使输入零中心并归一化，该算法需要评估每个输入的均值和标准差，通过评估当前小批次上的输入的均值和标准差(因此称为“批量归一化”)来做到这一点
\[\mu_B=\frac{1}{m_B}\sum^{m_B}_{i=1}x^{(i)}\\ \sigma^2_B=\frac{1}{m_B}\sum^{m_B}_{i=1}(x^{(i)}-\mu_B)^2\\ \hat x^{(x)}=\frac{x^{(i)}-\mu_B}{\sqrt{\sigma^2_B+\epsilon}}\\ z^{(i)}=\gamma 逐元素乘\hat x^{(i)}+\beta\\ \mu_B是输入的均值，在整个小批量B上评估\\ \sigma_B是输入向量的标准差\\ m_B是小批量中的实例数量\\ x^{(i)}是实例i的零中心和归一化向量\\ \gamma是该层的输出缩放参数向量\\ \beta是层的输出移动(偏移)参数向量(每个输入包含一个偏移参数)。每个输入都通过其相应的\\ 移动参数进行偏移\\ \epsilon是一个很小的数字，以避免被零除，这称为平滑项 \]- 在训练期间，BN会归一化其输入，然后重新缩放并偏移它们。但在测试期间，这不那么简单，我们可能需要对单个实例而不是成批次的实例做出预测。一种解决方法是等到训练结束，然后通过神经网络运行整个训练集，计算BN层每个输入的均值和标准差。然后在进行预测时，可以使用这些“最终”的输入均值和标准差，而不是一个批次的输入均值和标准差。然而，大多数批量归一化的实现都是通过使用该层输入的均值和标准差的移动平均值来估计训练期间的最终统计信息
- 批量归一化极大地改善了深度神经网络，消失梯度的问题已大大减少，以至于它们可以使用饱和的激活函数，例如tanh甚至逻辑激活函数。网络对权重初始化也不太敏感，可以使用更大的学习率，大大加快了学习过程
- 批量归一化的作用就像正则化一样，减少了对其他正则化技术的需求。但是批量归一化确实增加了模型的复杂性，由于每一层都需要额外的计算，因此神经网络的预测速度较慢，幸运的是，经常可以在训练后将BN层与上一层融合，从而避免了运行时的损失
- BN论文的作者主张在激活函数之前(而不是之后)添加BN层
- BN已经成为深度神经网络中最常用的层之一，以至于在图表中通常将其省略，因为假定在每层之后都添加了BN
-
梯度裁剪
- 缓解梯度爆炸问题的另一种流性技术是在反向创博期间裁剪梯度，使它们永远不会超过某个阈值，这称为梯度裁剪。这种技术最常用于循环神经网络，因为在RNN中难以使用批量归一化，对于其他网络，BN通常就足够了
- 在Keras中，实现梯度裁剪仅仅是一个在创建优化器时设置clipvalue或clipnorm参数的问题，该优化器会将梯度向量的每个分量都裁剪为-1.0和1.0之间，阈值是你可以调整的超参数，注意，它可能会改变梯度向量的方向。如果要确保“梯度裁剪”不更改梯度向量的方向，你应该通过设置clipnorm而不是clipvalue按照范数来裁剪
重用预训练层
- 从头开始训练非常大的DNN通常不是一个好主意：相反，你应该总是试图找到一个现有的与你要解决的任务更相似的神经网络，然后重用该网络的较低层。此技术称为迁移学习，它不仅会大大加快训练速度，而且会大大减少训练数据
- 如果新任务的输入图片的大小与原始任务中使用的图片不同，通常必须添加预处理步骤将其调整为原始模型所需的大小。一般而言，当输入具有类似的低级特征时，迁移学习最有效
- 通常应该替换掉原始模型的输出层，因为它对于新任务很可能根本没有用，甚至对于新任务而言可能没有正确数量的输出
- 任务越相似，可重用的层就越多(从较低的层开始)。对于非常相似的任务，请尝试保留所有的隐藏层和只是替换掉输出层
- 首先尝试冻结所有可重复使用的层(使其权重不可训练，这样梯度下降就不会对其进行修改)，训练模型并查看其表现。然后尝试解冻上部隐藏层中的一两层，使反向传播可以对其进行调整，再看性能是否有所提高。你拥有的训练数据越多，可以解冻的层就越多。当解冻重用层时，降低学习率也很有用，可以避免破坏其已经调整好的权重。如果你仍然无法获得良好的性能，并且你的训练数据很少，试着去掉顶部的隐藏层，然后再次冻结所有其余的隐藏层。你可以进行迭代，直到找到合适的可以重复使用的层数。如果你有大量的训练数据，则可以尝试替换顶部的隐藏层而不是去掉它们，你甚至可以添加更多的隐藏层
- 使用Keras进行迁移学习
- 为任务B训练model_B_on_A，但是由于新的输出层是随机初始化的，它会产生较大的错误(至少在前几个轮次内)，因此将存在较大的错误梯度，这可能会破坏重用的权重。为了避免这种情况，一种方法是在前几个轮次时冻结重用的层，给新层一些时间来学习合理的权重
- 冻结或解冻层后，你必须总是要编译模型
- 解冻重用层之后，降低学习率通常是个好主意，可以再次避免破坏重用的权重
- 事实证明，迁移学习在小型密集网络中不能很好地工作，大概是因为小型网络学习的模式很少，密集网络学习的是非常特定的模式，这在其他任务中不是很有用。迁移学习最适合使用深度卷积神经网络，该神经网络倾向于学习更为通用的特征检测器(尤其在较低层)
- 无监督预训练
- 假设你要处理一个没有太多标签训练数据的复杂任务，但不幸的是，你找不到在类似任务上训练的模型，则你可以执行无监督预训练，例如自动编码器或GAN。然后你可以重用自动编码器的较低层或GAN判别器的较低层，在顶部为你的任务添加输出层，并使用有监督学习来微调最终的网络
- 直到2010年，无监督预训练—通常使用受限的Boltzmann机器(RBM)—是深度网络的标准，只有在梯度消失问题得到解决后，使用有监督学习来训练DNN才变得更加普遍。无监督预训练今天通常使用自动编码器或GAN而不是RBM
- 辅助任务的预训练
- 如果你没有太多标记的训练数据，最后一个选择是在辅助任务上训练第一个神经网络，你可以轻松地为其获得或生成标记的数据，然后对实际任务重用该网络的较低层。第一个神经网络的较低层将学习特征检测器，第二个神经网络可能会重用这些特征检测器
- 例如，如果你要构建一个识别人脸的系统，每个人可能只有几张照片，显然不足以训练一个好的分类器。收集每个人的数百张图片不切实际。但是，你可以在网络上收集很多随机人物的图片，然后训练第一个神经网络来检测两个不同的图片是否是同一个人，这样的网络将会学习到很好的人脸特征检测器，因此重用其较低层可以使你用很少的训练数据俩训练一个好的人脸分类器
- 自我监督学习是指你从数据本身自动生成标签，然后使用有监督学习技术在所得到的“标签”数据集上训练模型。由于此方法不需要任何人工标记，因此最好将其分类为无监督学习的一种形式
更快的优化器
-
训练一个非常大的深度神经网络可能会非常缓慢。到目前为止，我们已经知道了四种加快训练速度(并获得了更好的解决方法)的方法：对连接权重应用一个良好的初始化策略，使用良好的激活函数，使用批量归一化，以及重用预训练网络的某些部分(可能建立在辅助任务上或使用无监督学习)。与常规的梯度下降优化器相比，使用更快的优化器也可以带来巨大的速度提升
-
动量优化
\[梯度下降通过直接减去权重的成本函数J(\theta)的梯度乘以学习率\eta(\nabla_{\theta}J(\theta))来更新权重\\ \theta。等式是\theta←\theta-\eta\nabla_{\theta J(\theta)}。它不关心较早的梯度是什么，如果局部梯度\\ 很小，则它会走得非常慢 \]- 动量算法非常关心先前的梯度是什么：在每次迭代时，它都会从动量向量m(乘以学习率η)中减去局部梯度，并通过添加该动量向量来更新权重。换句话说，梯度是用于加速度而不是速度。为了模拟某种摩擦机制并防止动量变得过大，该算法引入了一个新的超参数β，称为动量，必须将其设置为0(高摩擦)和1(无摩擦)之间，典型的动量值是0.9
\[m←\beta m - \eta \nabla_{\theta} J(\theta)\\ \theta←\theta + m \]- 如果梯度保持恒定，则最终速度(即权重更新的最大大小)等于该梯度乘以学习率η再乘以1/(1-β)(忽略符号)。这使动量优化比梯度下降要更快地从平台逃脱。梯度下降相当快地沿着陡峭的斜坡下降，但是沿着山谷下降需要更多时间。相反，动量优化将沿着山谷滚动得越来越快，直到达到谷底(最优解)。在使用批量归一化的深层神经网络中，较高的层通常会得到比例不同的输入，因此使用动量优化会有所帮助，它还可以帮助绕过局部优化问题
- 由于这种动量势头，优化器可能会稍微过调，然后又回来，再次过调，在稳定于最小点之前会多次震荡。这是在系统中有些摩擦力的原因之一：它消除了这些震荡，从而加快了收敛速度
-
Nesterov加速梯度
-
Nesterov加速梯度(NAG)是动量优化的一个小变体，几乎总是比原始动量优化要快。它不是在局部位置θ，而是在θ+βm处沿动量方向稍微提前处测量成本函数的梯度
\[m ←\beta m-\eta\nabla_{\theta}J(\theta+\beta m)\\ \theta ← \theta + m \] -
这种小的调整有效是因为通常动量向量会指向正确的方向(即朝向最优解)，因此使用在该方向上测得的更远的梯度而不是原始位置上的梯度会稍微准确一些
-
NAG通常比常规动量优化更快
-
常规与Nesterov动量优化相比：前者使用在动量步骤之前计算的梯度，而后者使用在动量步骤之后计算的梯度
-
-
AdaGrad
- 再次考虑拉长的碗装问题：梯度下降从快速沿最陡的坡度下降开始，该坡度没有直接指向全局最优解，然后非常缓慢地下降到谷底。如果算法可以更早地纠正其方向，使它更多地指向全局最优解，那将是很好的。AdaGrad算法通过沿最陡峭的维度按比例缩小梯度向量来实现词矫正
\[s ← s + \nabla_{\theta}J(\theta) 逐元素相乘 \nabla_{\theta}J(\theta)\\ 此向量形式等效于针对向量s中的每个元素s_i计算s_i←s_i+(\partial J(\theta)/\partial \theta_i)^2\\ 换句话说，每个s_i累加关于参数\theta_i的成本函数偏导数的平方\\ 如果成本函数沿第i个维度陡峭，则s_i将在每次迭代中变得越来越大\\ \theta ← \theta-\eta\nabla_{\theta}J(\theta) 逐元素相除 \sqrt{s+\epsilon} \]- 该算法会降低学习率，但是对于陡峭的维度，它的执行速度要比对缓慢下降的维度的执行速度要快。这称为自适应学习率，它有助于将结果更新更直接地指向全局最优解。另一个好处是，它几乎不需要调整学习率η
- 对于简单的二次问题，AdaGrad经常表现良好，但是在训练神经网络时，它往往停止得太早，学习率被按比例缩小，以至于算法在最终达到全局最优解之前完全停止了。因此，及时Keras有AdaGrad优化器，你也不应使用它来训练深度神经网络
-
RMSProp
- AdaGrad有下降太快，永远不会收敛到全局最优解的风险，RMSProp算法通过只是累加最近迭代中的梯度(而不是自训练开始以来的所有梯度)来解决这个问题，它通过在第一步中使用指数衰减来实现
\[s←\beta s+(1-\beta)\nabla_{\theta}J(\theta) 逐元素相乘\nabla J(\theta)\\ \theta ← \theta - \eta \nabla _{\theta}J(\theta)逐元素相除\sqrt{s+\epsilon} \]- 衰减率β通常设置为0.9，除了简单的问题外该优化器几乎总是比AdaGrad表现更好
-
Adam和Nadam优化
- Adam代表自适应矩估计，结合了动量优化和RMSProp的思想：就像动量优化一样，它跟踪过去梯度的指数衰减平均值。就像RMSProp一样，它跟踪过去平方梯度的指数衰减平均值
\[m←\beta_1m-(1-\beta_1)\nabla_{\theta}J(\theta)\\ s←\beta_2s+(1-\beta_2)\nabla_{\theta}J(\theta)逐元素相乘\nabla_{\theta}J(\theta)\\ \hat m ← \frac{m}{1-\beta^t_1}\\ \hat s← \frac{s}{1-\beta^t_2}\\ \theta←\theta - \eta\hat m 逐元素相除\sqrt{\hat s + \epsilon}\\ 其中t表示迭代次数(从1开始) \]- 动量衰减超参数β1通常被初始化为0.9，而缩放衰减超参数β2通常被初始化为0.999
- 由于Adam是一种自适应学习算法(如AdaGrad和RMSProp)，因此对学习率超参数η需要较少的调整。你通常可以使用默认值η=0.001，这使得Adam甚至比梯度下降更易于使用
-
AdaMax
\[AdaMax将l_2范数替换为l_∞范数。具体来说，它用s←max(\beta_2s,\nabla_{\theta}J(\theta))替换上述\\ 公式的步骤2，删除步骤4，在第5步中，将梯度更新按比例s缩小，这是时间衰减梯度的最大值。\\ 实际上，这可以使AdaMax比Adam更稳定，但这确实取决于数据集，通常Adam的表现更好 \] -
Nadam
- Nadam优化是Adam优化加上Nesterov技巧，因此其收敛速度通常比Adam稍快
-
优化器比较
| 类别 | 收敛速度 | 收敛质量 |
|---|---|---|
| SGD | * | *** |
| SGD(momentum=...) | ** | *** |
| SGD(momentum=...,nesterov=True) | ** | *** |
| AdaGrad | *** | *(停止太早) |
| RMSProp | *** | ** 或者*** |
| Adam | *** | ** 或者*** |
| Nadam | *** | ** 或者*** |
| AdaMax | *** | ** 或者*** |
学习率调度
- 找到一个好的学习率非常重要。如果你设置得太高，训练可能会发散。如果你设置得太低，训练最终会收敛到最优解，但是这将花费很长时间。如果将它设置得稍微有点高，它一开始会很快，但是最终会围绕最优解震荡，不会真正稳定下来，如果你的计算力预算有限，则可能必须先中断训练，然后才能正确收敛，从而产生次优解决
- 如果你从一个较大的学习率开始，一旦训练没有取得进展后就降低它，那与恒定学习率相比，你就可以更快地找到一个最优解。从低学习率开始，增加它，然后再降低它也是有好处的，这些策略称为学习率调度
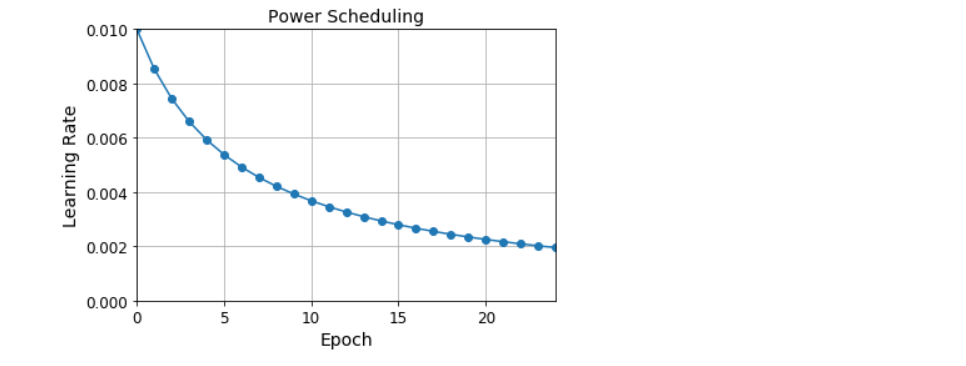
- 幂调度
- 将学习率设置为迭代次数t的函数：η(t)=η0/(1+t/s)c。初始学习率η0、幂c(通常设置为1)和步骤s是超参数。学习率再每一步都会下降。在s个步骤之后，它下降到η0/2。再在s个步骤后，它下降到η0/3，然就下降到η0/4，然后是η0/5，以此类推。此调度开始迅速下降，然后越来越慢
- 指数调度
- 将学习速率设置为η(t)=η00.1t/s。学习率每s步将逐渐下降10倍。幂调度越来越缓慢地降低学习率，而指数调度则使学习率每s步都降低10倍
- 分段恒定调度
- 对一些轮次使用恒定的学习率，对于另外一些轮次使用较小的学习率，以此类推
- 性能调度
- 每N步测量一次验证误差(就像提前停止一样)，并且当误差停止下降时，将学习率降低λ倍
- 1周期调度
- 1周期调度从提高初始学习率η0开始，在训练中途线性增长至η1。然后，它在训练的后半部分将学习率再次线性降低到η0，通过将学习率降低几个数量级(仍然是线性的)来完成最后几个轮次
- 幂调度
通过正则化避免过拟合
- 有了4个参数，我可以拟合出一头大象，有了5个参数我可以让它摆动鼻子
- l1和l2正则化
- 就像对简单线性模型所做的一样，可以使用l2正则化来约束神经网络的连接权重，如果想要稀疏模型则可以使用l1正则化
- dropout
- 对深度神经网络，dropout是最受欢迎的正则化技术之一，只需要增加dropout，即使最先进的神经网络也能获得1%-2%的准确率提升
- 在每个训练步骤中，每个神经元(包括输入神经元，但始终不包括输出神经元)都有暂时“删除”的概率p，这意味着在这个训练步骤中它被完全忽略，但在下一步中可能处于活动状态。超参数p称为dropout率，通常设置为10%到50%：在循环神经网络中接近20%-30%，在卷积神经网络中接近40%-50%，训练后，神经元不在被删除。
- 经过dropout训练的神经元不能与其相邻的神经元相互适应，它们必须自己发挥最大的作用。它们也不能过分依赖少数输入神经元，它们必须注意每个输入神经元。它们最终对输入的微小变化不太敏感。最后你将获得一个更有鲁棒性的网络，该网络有更好的泛化能力
- 在实践中，你通常只可以对第一层至第三层(不包括输出层)中的神经元应用dropout。训练后，需要将每个输入连接权重乘以保留高绿(1-p)，或者我们可以在训练过程中将每个神经元的输出除以保留概率(在测试过程中是不dropout的)
- 如果你发现模型过拟合，则可以提高dropout率，如果模型欠拟合，则应尝试降低dropout率
- 如果要基于SELU激活函数对自归一化网络进行正则化，则应使用alpha dropout：这是dropout的一种变体，它保留了其输入的均值和标注差(因为常规的dropout会破坏自归一化)
- 蒙特卡罗(MC)dropout
- 该技术可以提高任何训练后的dropout模型的性能，而无需重新训练甚至根本不用修改它，它可以更好地测量模型的不确定性，并且实现起来非常简单
- 对测试集进行n个预测，设置training=Ture来确保dropout层处于激活状态，然后把预测堆叠起来。由于dropout处于激活状态，因此所有预测都将有所不同。概括来说，对具有dropout功能的多个预测进行平均，这使蒙特卡罗估计比通常关闭dropout的单个预测的结果更可靠
- 简而言之，MC Dropout是一种出色的技术，可以提升dropout模型并提供更好的不确定性估计，当然，由于这只是训练期间的常规dropout，所以它也像正则化函数
- 最大范数正则化
\[对于神经网络而言，另一种流行的正则化技术称为最大范数正则化：对于每个神经元，\\
它会限制传入连接的权重w，使得||w||_2<=r，其中r是最大范数超参数，\\
||·||_2是l_2范数\\
最大范数正则化不会把正则化损失项添加到总体损失函数中。取而代之的是，\\
通常在每个训练步骤后通过计算||w||_2来实现，如有需要，请重新缩放\\
w(w←w\frac{r}{||w||_2})\\
减小r会增加正则化的数量，并有助于减少过拟合。最大范数正则化还可以帮助\\
缓解不稳定的梯度问题(如果你未使用“批量归一化”)
\]
总结和实用指南
- 默认的DNN配置
| 超参数 | 默认值 |
|---|---|
| 内核初始化 | He初始化 |
| 激活函数 | ELU |
| 归一化 | 浅层网络：不需要；深度网络：批量归一化 |
| 正则化 | 提前停止(如果需要，可加l2) |
| 优化器 | 动量优化(或RMSProp或Nadam) |
| 学习率调度 | 1周期 |
- 用于自归一化网络的DNN配置
| 超参数 | 默认值 |
|---|---|
| 内核初始化 | LeCun初始化 |
| 激活函数 | SELU |
| 归一化 | 不需要(自归一化) |
| 正则化 | 如果需要：Alpha dropout |
| 优化器 | 动量优化(或RMSProp或Nadam) |
| 学习率调度 | 1周期 |
代码部分
引入
import sys
assert sys.version_info >= (3, 5)
import sklearn
assert sklearn.__version__ >= '0.20'
try:
%tensorflow_version 2.x
except Exception as e:
pass
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= '2.0'
%load_ext tensorboard
import numpy as np
import os
np.random.seed(42)
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
PROJECT_ROOT_DIR = '.'
CHAPTER_ID = 'deep'
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, 'images', CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension='png', resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + '.' + fig_extension)
print('Saving figure', fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
梯度消失/梯度爆炸问题
def logit(z):
return 1 / (1 + np.exp(-z))
z = np.linspace(-5, 5, 200)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [1, 1], 'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot([-5, 5], [-3/4, 7/4], 'g--')
plt.plot(z, logit(z), 'b-', linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha='center')
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha='center')
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha='center')
plt.grid(True)
plt.title('Sigmoid activation function', fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig('sigmoid_saturation_plot')
plt.show()
He初始化
[name for name in dir(keras.initializers) if not name.startswith('_')]
'''
['Constant',
'GlorotNormal',
'GlorotUniform',
'HeNormal',
'HeUniform',
'Identity',
'Initializer',
'LecunNormal',
'LecunUniform',
'Ones',
'Orthogonal',
'RandomNormal',
'RandomUniform',
'TruncatedNormal',
'VarianceScaling',
'Zeros',
'constant',
'deserialize',
'get',
'glorot_normal',
'glorot_uniform',
'he_normal',
'he_uniform',
'identity',
'lecun_normal',
'lecun_uniform',
'ones',
'orthogonal',
'random_normal',
'random_uniform',
'serialize',
'truncated_normal',
'variance_scaling',
'zeros']
'''
keras.layers.Dense(10, activation='relu', kernel_initializer='he_normal') # <keras.layers.core.Dense at 0x15a3a0d0b70>
init = keras.initializers.VarianceScaling(scale=2, mode='fan_avg', distribution='uniform')
keras.layers.Dense(10, activation='relu', kernel_initializer=init) # <keras.layers.core.Dense at 0x15a3a0f9fd0>
非饱和激活函数
# leaky ReLU
def leaky_relu(z, alpha=0.01):
return np.maximum(alpha*z, z)
plt.plot(z, leaky_relu(z, 0.05), 'b-', linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([0, 0], [-0.5, 4.2], 'k-')
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5), xy=(-5, -0.2), arrowprops=props, fontsize=14, ha='center')
plt.title('Leaky ReLU activation function', fontsize=14)
plt.axis([-5, 5, -0.5, 4.2])
save_fig('leaky_relu_plot')
plt.show()
[m for m in dir(keras.activations) if not m.startswith('_')]
'''
['deserialize',
'elu',
'exponential',
'gelu',
'get',
'hard_sigmoid',
'linear',
'relu',
'selu',
'serialize',
'sigmoid',
'softmax',
'softplus',
'softsign',
'swish',
'tanh']
'''
[m for m in dir(keras.layers) if 'relu' in m.lower()] # ['LeakyReLU', 'PReLU', 'ReLU', 'ThresholdedReLU']
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full / 255.0
X_test = X_test / 255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer='he_normal'),
keras.layers.LeakyReLU(),
keras.layers.Dense(100, kernel_initializer='he_normal'),
keras.layers.LeakyReLU(),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
# PReLU
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer='he_normal'),
keras.layers.PReLU(),
keras.layers.Dense(100, kernel_initializer='he_normal'),
keras.layers.PReLU(),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
# ELU
def elu(z, alpha=1):
return np.where(z < 0, alpha * (np.exp(z) - 1), z)
plt.plot(z, elu(z), 'b-', linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1, -1], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title(r'ELU activation function ($\alpha=1$)', fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig('elu_plot')
plt.show()
keras.layers.Dense(10, activation='elu') # <keras.layers.core.Dense at 0x15a3a14dd68>
# SELU
from scipy.special import erfc
alpha_0_1 = -np.sqrt(2 / np.pi) / (erfc(1/np.sqrt(2)) * np.exp(1/2) - 1)
scale_0_1 = (1 - erfc(1 / np.sqrt(2)) * np.sqrt(np.e)) * np.sqrt(2 * np.pi) * (2 * erfc(np.sqrt(2))*np.e**2 + np.pi*erfc(1/np.sqrt(2))**2*np.e - 2*(2+np.pi)*erfc(1/np.sqrt(2))*np.sqrt(np.e)+np.pi+2)**(-1/2)
def selu(z, scale=scale_0_1, alpha=alpha_0_1):
return scale * elu(z, alpha)
plt.plot(z, selu(z), 'b-', linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1.758, -1.758], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title('SELU activation function', fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig('selu_plot')
plt.show()
# Using this activation function, even a 1,000 layer deep neural network
# preserves roughly mean 0 and standard deviation 1 across all layers,
# avoiding the exploding/vanishing gradients problem:
np.random.seed(42)
Z = np.random.normal(size=(500, 100)) # standardized inputs
for layer in range(1000):
W = np.random.normal(size=(100, 100), scale=np.sqrt(1 / 100)) # LeCun initialization
Z = selu(np.dot(Z, W))
means = np.mean(Z, axis=0).mean()
stds = np.std(Z, axis=0).mean()
if layer % 100 == 0:
print('Layer {}: mean {:.2f}, std deviation {:.2f}'.format(layer, means, stds))
'''
Layer 0: mean -0.00, std deviation 1.00
Layer 100: mean 0.02, std deviation 0.96
Layer 200: mean 0.01, std deviation 0.90
Layer 300: mean -0.02, std deviation 0.92
Layer 400: mean 0.05, std deviation 0.89
Layer 500: mean 0.01, std deviation 0.93
Layer 600: mean 0.02, std deviation 0.92
Layer 700: mean -0.02, std deviation 0.90
Layer 800: mean 0.05, std deviation 0.83
Layer 900: mean 0.02, std deviation 1.00
'''
keras.layers.Dense(10, activation='selu', kernel_initializer='lecun_normal') # <keras.layers.core.Dense at 0x15a3e760358>
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'))
for layer in range(99):
model.add(keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
# 中心化&标准化
pixel_means = X_train.mean(axis=0, keepdims=True)
pixel_stds = X_train.std(axis=0, keepdims=True)
X_train_scaled = (X_train - pixel_means) / pixel_stds
X_valid_scaled = (X_valid - pixel_means) / pixel_stds
X_test_scaled = (X_test - pixel_means) / pixel_stds
history = model.fit(X_train_scaled, y_train, epochs=5, validation_data=(X_valid_scaled, y_valid))
# 使用ReLU对比
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation='relu', kernel_initializer='he_normal'))
for layer in range(99):
model.add(keras.layers.Dense(100, activation='relu', kernel_initializer='he_normal'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model.fit(X_train_scaled, y_train, epochs=5, validation_data=(X_valid_scaled, y_valid))
批量归一化
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation='relu'),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation='relu'),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation='softmax')
])
model.summary()
'''
Model: "sequential_6"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_6 (Flatten) (None, 784) 0
_________________________________________________________________
batch_normalization (BatchNo (None, 784) 3136
_________________________________________________________________
dense_415 (Dense) (None, 300) 235500
_________________________________________________________________
batch_normalization_1 (Batch (None, 300) 1200
_________________________________________________________________
dense_416 (Dense) (None, 100) 30100
_________________________________________________________________
batch_normalization_2 (Batch (None, 100) 400
_________________________________________________________________
dense_417 (Dense) (None, 10) 1010
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
_________________________________________________________________
'''
bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]
'''
[('batch_normalization/gamma:0', True),
('batch_normalization/beta:0', True),
('batch_normalization/moving_mean:0', False),
('batch_normalization/moving_variance:0', False)]
'''
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation('relu'),
keras.layers.Dense(100, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation('relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
梯度裁剪
optimizer = keras.optimizers.SGD(clipvalue=1.0)
optimizer = keras.optimizers.SGD(clipnorm=1.0)
重用预训练层
def split_dataset(X, y):
y_5_or_6 = (y == 5) | (y == 6)
y_A = y[~y_5_or_6]
y_A[y_A > 6] -= 2
y_B = (y[y_5_or_6] == 6).astype(np.float32)
return ((X[~y_5_or_6], y_A), (X[y_5_or_6], y_B))
(X_train_A, y_train_A), (X_train_B, y_train_B) = split_dataset(X_train, y_train)
(X_valid_A, y_valid_A), (X_valid_B, y_valid_B) = split_dataset(X_valid, y_valid)
(X_test_A, y_test_A), (X_test_B, y_test_B) = split_dataset(X_test, y_test)
X_train_B = X_train_B[:200]
y_train_B = y_train_B[:200]
X_train_A.shape # (43986, 28, 28)
X_train_B.shape # (200, 28, 28)
y_train_A[:30]
'''
array([4, 0, 5, 7, 7, 7, 4, 4, 3, 4, 0, 1, 6, 3, 4, 3, 2, 6, 5, 3, 4, 5,
1, 3, 4, 2, 0, 6, 7, 1], dtype=uint8)
'''
y_train_B[:30]
'''
array([1., 1., 0., 0., 0., 0., 1., 1., 1., 0., 0., 1., 1., 0., 0., 0., 0.,
0., 0., 1., 1., 0., 0., 1., 1., 0., 1., 1., 1., 1.], dtype=float32)
'''
tf.random.set_seed(42)
np.random.seed(42)
model_A = keras.models.Sequential()
model_A.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_A.add(keras.layers.Dense(n_hidden, activation='selu'))
model_A.add(keras.layers.Dense(8, activation='softmax'))
model_A.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model_A.fit(X_train_A, y_train_A, epochs=20, validation_data=(X_valid_A, y_valid_A))
model_A.save('my_model_A.h5')
model_B = keras.models.Sequential()
model_B.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_B.add(keras.layers.Dense(n_hidden, activation='selu'))
model_B.add(keras.layers.Dense(1, activation='sigmoid'))
model_B.compile(loss='binary_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model_B.fit(X_train_B, y_train_B, epochs=20, validation_data=(X_valid_B, y_valid_B))
model_B.summary()
'''
Model: "sequential_11"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_11 (Flatten) (None, 784) 0
_________________________________________________________________
dense_436 (Dense) (None, 300) 235500
_________________________________________________________________
dense_437 (Dense) (None, 100) 30100
_________________________________________________________________
dense_438 (Dense) (None, 50) 5050
_________________________________________________________________
dense_439 (Dense) (None, 50) 2550
_________________________________________________________________
dense_440 (Dense) (None, 50) 2550
_________________________________________________________________
dense_441 (Dense) (None, 1) 51
=================================================================
Total params: 275,801
Trainable params: 275,801
Non-trainable params: 0
_________________________________________________________________
'''
model_A = keras.models.load_model('my_model_A.h5')
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation='sigmoid'))
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss='binary_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4, validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True
model_B_on_A.compile(loss='binary_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16, validation_data=(X_valid_B, y_valid_B))
model_B.evaluate(X_test_B, y_test_B) # [0.08957738429307938, 0.9860000014305115]
model_B_on_A.evaluate(X_test_B, y_test_B) # [0.060371216386556625, 0.9909999966621399]
(100 - 98.6) / (100 - 99.1) # 1.555555555555552
更快的优化器
# 动量优化
optimizer = keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)
# Nesterov加速梯度
optimizer = keras.optimizers.SGD(learning_rate=0.01, momentum=0.9, nesterov=True)
# AdaGrad
optimizer = keras.optimizers.Adagrad(learning_rate=0.001)
# RMSProp
optimizer = keras.optimizers.RMSprop(learning_rate=0.001, rho=0.9)
# Adam
optimizer = keras.optimizers.Adam(learning_rate=0.001, beta_1=0.9, beta_2=0.999)
# AdaMax
optimizer = keras.optimizers.Adamax(learning_rate=0.001, beta_1=0.9, beta_2=0.999)
# Nadam
optimizer = keras.optimizers.Nadam(learning_rate=0.001, beta_1=0.9, beta_2=0.999)
学习率调度
# 幂调度
optimizer = keras.optimizers.SGD(learning_rate=0.01, decay=1e-4)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
import math
learning_rate = 0.01
decay = 1e-4
batch_size = 32
n_steps_per_epoch = math.ceil(len(X_train) / batch_size)
epochs = np.arange(n_epochs)
lrs = learning_rate / (1 + decay * epochs * n_steps_per_epoch)
plt.plot(epochs, lrs, 'o-')
plt.axis([0, n_epochs - 1, 0, 0.01])
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.title('Power Scheduling', fontsize=14)
plt.grid(True)
plt.show()
# 指数调度
def exponential_decay_fn(epoch):
return 0.01 * 0.1 ** (epoch / 20)
# 闭包
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1 ** (epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics=['accuracy'])
n_epochs = 25
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid), callbacks=[lr_scheduler])
plt.plot(history.epoch, history.history['lr'], 'o-')
plt.axis([0, n_epochs - 1, 0, 0.011])
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.title('Exponential Scheduling', fontsize=14)
plt.grid(True)
plt.show()
# 在每一步更新学习率
def exponential_decay_fn(epoch, lr):
return lr * 0.1 ** (1 / 20)
K = keras.backend
class ExponentialDecay(keras.callbacks.Callback):
def __init__(self, s=4000):
super().__init__()
self.s = s
def on_batch_begin(self, batch, logs=None):
lr = K.get_value(self.model.optimizer.learning_rate)
K.set_value(self.model.optimizer.learning_rate, lr * 0.1 ** (1 / s))
def on_epoch_end(self, epoch, logs=None):
logs = logs or {}
logs['lr'] = K.get_value(self.model.optimizer.learning_rate)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
lr0 = 0.01
optimizer = keras.optimizers.Nadam(learning_rate=lr0)
model.compile(loss='sparse_categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
n_epochs = 25
s = 20 * len(X_train) // 32
exp_decay = ExponentialDecay(s)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid), callbacks=[exp_decay])
n_steps = n_epochs * len(X_train) // 32
steps = np.arange(n_steps)
lrs = lr0 * 0.1 ** (steps / s)
plt.plot(steps, lrs, '-', linewidth=2)
plt.axis([0, n_steps - 1, 0, lr0 * 1.1])
plt.xlabel('Batch')
plt.ylabel('Learning Rate')
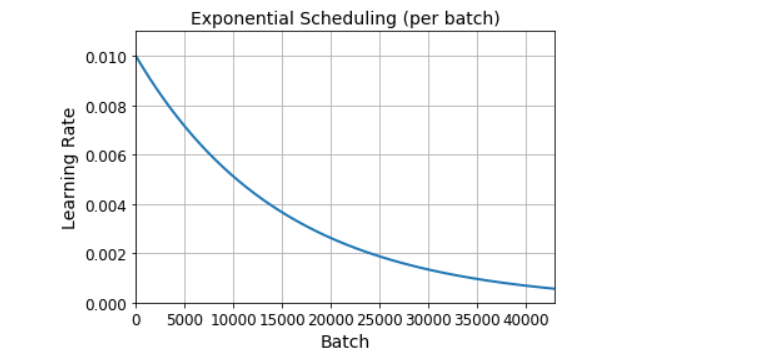
plt.title('Exponential Scheduling (per batch)', fontsize=14)
plt.grid(True)
plt.show()
# 分段恒定调度
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001
def piecewise_constant(boundaries, values):
boundaries = np.array([0] + boundaries)
values = np.array(values)
def piecewise_constant_fn(epoch):
return values[np.argmax(boundaries > epoch) -1]
return piecewise_constant_fn
piecewise_constant_fn = piecewise_constant([5, 15], [0.01, 0.005, 0.001])
lr_scheduler = keras.callbacks.LearningRateScheduler(piecewise_constant_fn)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics=['accuracy'])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid), callbacks=[lr_scheduler])
plt.plot(history.epoch, [piecewise_constant_fn(epoch) for epoch in history.epoch], 'o-')
plt.axis([0, n_epochs - 1, 0, 0.011])
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.title('Piecewise Constant Scheduling', fontsize=14)
plt.grid(True)
plt.show()
# 性能调度
tf.random.set_seed(42)
np.random.seed(42)
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
optimizer = keras.optimizers.SGD(learning_rate=0.02, momentum=0.9)
model.compile(loss='sparse_categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid), callbacks=[lr_scheduler])
plt.plot(history.epoch, history.history['lr'], 'bo-')
plt.xlabel('Epoch')
plt.ylabel('Learning Rate', color='b')
plt.tick_params('y', colors='b')
plt.gca().set_xlim(0, n_epochs - 1)
plt.grid(True)
ax2 = plt.gca().twinx()
ax2.plot(history.epoch, history.history['val_loss'], 'r^-')
ax2.set_ylabel('Validation Loss', color='r')
ax2.tick_params('y', colors='r')
plt.title('Reduce LR on Plateau', fontsize=14)
plt.show()
# tf.keras schedulers
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
s = 20 * len(X_train) // 32
learning_rate = keras.optimizers.schedules.ExponentialDecay(0.01, s, 0.1)
optimizer = keras.optimizers.SGD(learning_rate)
model.compile(loss='sparse_categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
# 对于分段恒定调度
learning_rate = keras.optimizers.schedules.PiecewiseConstantDecay(
boundaries = [5. * n_steps_per_epoch, 15. * n_steps_per_epoch],
values = [0.01, 0.005, 0.001]
)
# 1周期调度
K = keras.backend
class ExponentialLearningRate(keras.callbacks.Callback):
def __init__(self, factor):
self.factor = factor
self.rates = []
self.losses = []
def on_batch_end(self, batch, logs):
self.rates.append(K.get_value(self.model.optimizer.learning_rate))
self.losses.append(logs['loss'])
K.set_value(self.model.optimizer.learning_rate, self.model.optimizer.learning_rate * self.factor)
def find_learning_rate(model, X, y, epochs=1, batch_size=32, min_rate=10**-5, max_rate=10):
init_weights = model.get_weights()
iterations = math.ceil(len(X) / batch_size) * epochs
factor = np.exp(np.log(max_rate / min_rate) / iterations)
init_lr = K.get_value(model.optimizer.learning_rate)
K.set_value(model.optimizer.learning_rate, min_rate)
exp_lr = ExponentialLearningRate(factor)
history = model.fit(X, y, epochs=epochs, batch_size=batch_size, callbacks=[exp_lr])
K.set_value(model.optimizer.learning_rate, init_lr)
model.set_weights(init_weights)
return exp_lr.rates, exp_lr.losses
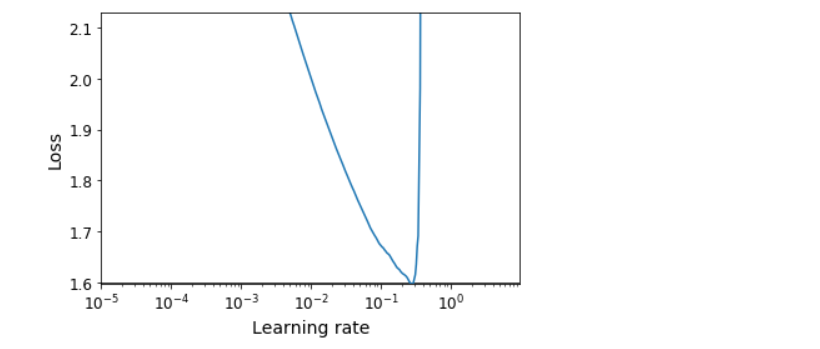
def plot_lr_vs_loss(rates, losses):
plt.plot(rates, losses)
plt.gca().set_xscale('log')
plt.hlines(min(losses), min(rates), max(rates))
plt.axis([min(rates), max(rates), min(losses), (losses[0] + min(losses)) / 2])
plt.xlabel('Learning rate')
plt.ylabel('Loss')
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer=keras.optimizers.SGD(learning_rate=1e-3), metrics=['accuracy'])
batch_size = 128
rates, losses = find_learning_rate(model, X_train_scaled, y_train, epochs=1, batch_size=batch_size)
plot_lr_vs_loss(rates, losses)
class OneCycleScheduler(keras.callbacks.Callback):
def __init__(self, iterations, max_rate, start_rate=None, last_iteration=None, last_rate=None):
self.iterations = iterations
self.max_rate = max_rate
self.start_rate = start_rate or max_rate / 10
self.last_iteration = last_iteration or iterations // 10 + 1
self.half_iteration = (iterations - self.last_iteration) // 2
self.last_rate = last_rate or self.start_rate / 1000
self.iteration = 0
def _interpolate(self, iter1, iter2, rate1, rate2):
return ((rate2 - rate1) * (self.iteration - iter1) / (iter2 - iter1) + rate1)
def on_batch_begin(self, batch, logs):
if self.iteration < self.half_iteration:
rate = self._interpolate(0, self.half_iteration, self.start_rate, self.max_rate)
elif self.iteration < 2 * self.half_iteration:
rate = self._interpolate(self.half_iteration, 2 * self.half_iteration, self.max_rate, self.start_rate)
else:
rate = self._interpolate(2 * self.half_iteration, self.iterations, self.start_rate, self.last_rate)
self.iteration += 1
K.set_value(self.model.optimizer.learning_rate, rate)
n_epochs = 25
onecycle = OneCycleScheduler(math.ceil(len(X_train) / batch_size) * n_epochs, max_rate=0.05)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, batch_size=batch_size, validation_data=(X_valid_scaled, y_valid), callbacks=[onecycle])
正则化避免过拟合
# l1和l2正则化
layer = keras.layers.Dense(100, activation='elu', kernel_initializer='he_normal', kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation='elu', kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(0.01)),
keras.layers.Dense(100, activation='elu', kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(0.01)),
keras.layers.Dense(10, activation='softmax', kernel_regularizer=keras.regularizers.l2(0.01))
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics='accuracy')
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
from functools import partial
RegularizedDense = partial(keras.layers.Dense, activation='elu', kernel_initializer='he_normal',
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics=['accuracy'])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
# Dropout
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation='elu', kernel_initializer='he_normal'),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation='elu', kernel_initializer='he_normal'),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics=['accuracy'])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
# Alpha Dropout
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(300, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal'),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation='softmax')
])
optimizer = keras.optimizers.SGD(learning_rate=0.01, momentum=0.9, nesterov=True)
model.compile(loss='sparse_categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
n_epochs = 20
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test) # [0.4866867661476135, 0.8493000268936157]
model.evaluate(X_train_scaled, y_train) # [0.3851325213909149, 0.8676000237464905]
# MC Dropout
tf.random.set_seed(42)
np.random.seed(42)
y_probas = np.stack([model(X_test_scaled, training=True) for sample in range(100)])
y_proba = y_probas.mean(axis=0)
y_std = y_probas.std(axis=0)
np.round(model.predict(X_test_scaled[:1]), 2)
'''
array([[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.03, 0. , 0.94]],
dtype=float32)
'''
np.round(y_probas[:, :1], 2)
'''
array([[[0. , 0. , 0. , 0. , 0. , 0.05, 0. , 0.67, 0. , 0.28]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.09, 0. , 0.87]],
[[0. , 0. , 0. , 0. , 0. , 0.17, 0. , 0.62, 0. , 0.21]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.04, 0. , 0.92]],
[[0. , 0. , 0. , 0. , 0. , 0.21, 0. , 0.61, 0. , 0.18]],
[[0. , 0. , 0. , 0. , 0. , 0.18, 0. , 0.34, 0. , 0.48]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.96, 0. , 0.02]],
[[0. , 0. , 0. , 0. , 0. , 0.17, 0. , 0.06, 0. , 0.77]],
[[0. , 0. , 0. , 0. , 0. , 0.22, 0. , 0.02, 0. , 0.76]],
[[0. , 0. , 0. , 0. , 0. , 0.24, 0. , 0.24, 0. , 0.52]],
[[0. , 0. , 0. , 0. , 0. , 0.07, 0. , 0.14, 0. , 0.79]],
[[0. , 0. , 0. , 0. , 0. , 0.36, 0. , 0.45, 0.03, 0.16]],
[[0. , 0. , 0. , 0. , 0. , 0.33, 0. , 0.15, 0. , 0.51]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.64, 0. , 0.32]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.02, 0. , 0.97]],
[[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.47, 0. , 0.5 ]],
[[0. , 0. , 0.01, 0. , 0. , 0.22, 0. , 0.33, 0. , 0.43]],
[[0. , 0. , 0. , 0. , 0. , 0.62, 0. , 0.04, 0. , 0.33]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.9 , 0. , 0.06]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.18, 0. , 0.8 ]],
[[0. , 0. , 0. , 0. , 0. , 0.32, 0. , 0.49, 0. , 0.19]],
[[0. , 0. , 0. , 0. , 0. , 0.19, 0. , 0.56, 0. , 0.25]],
[[0. , 0. , 0. , 0. , 0. , 0.06, 0. , 0.38, 0. , 0.56]],
[[0. , 0. , 0. , 0. , 0. , 0.24, 0. , 0.15, 0. , 0.61]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.01, 0. , 0.97]],
[[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.12, 0. , 0.85]],
[[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.11, 0. , 0.89]],
[[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.81, 0. , 0.17]],
[[0. , 0. , 0. , 0. , 0. , 0.22, 0. , 0.32, 0. , 0.45]],
[[0. , 0. , 0. , 0. , 0. , 0.89, 0. , 0.07, 0. , 0.04]],
[[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.47, 0. , 0.5 ]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.17, 0. , 0.79]],
[[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.99, 0. , 0.01]],
[[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.03, 0. , 0.94]],
[[0. , 0. , 0. , 0. , 0. , 0.37, 0. , 0.16, 0. , 0.46]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.01, 0. , 0.98]],
[[0. , 0. , 0. , 0. , 0. , 0.08, 0. , 0.02, 0. , 0.89]],
[[0. , 0. , 0. , 0. , 0. , 0.26, 0. , 0.58, 0. , 0.16]],
[[0. , 0. , 0. , 0. , 0. , 0.73, 0. , 0.17, 0. , 0.1 ]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.16, 0. , 0.82]],
[[0. , 0. , 0. , 0. , 0. , 0.36, 0. , 0.02, 0. , 0.62]],
[[0. , 0. , 0. , 0. , 0. , 0.14, 0. , 0.34, 0. , 0.52]],
[[0. , 0. , 0. , 0. , 0. , 0.86, 0. , 0.05, 0. , 0.08]],
[[0. , 0. , 0. , 0. , 0. , 0.11, 0. , 0. , 0. , 0.89]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.01, 0. , 0.98]],
[[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.84, 0. , 0.13]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.98, 0. , 0. ]],
[[0. , 0. , 0. , 0. , 0. , 0.5 , 0. , 0.1 , 0. , 0.4 ]],
[[0. , 0. , 0. , 0. , 0. , 0.64, 0. , 0.03, 0. , 0.33]],
[[0. , 0. , 0. , 0. , 0. , 0.84, 0. , 0.06, 0. , 0.11]],
[[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.09, 0. , 0.91]],
[[0. , 0. , 0. , 0. , 0. , 0.16, 0. , 0.02, 0. , 0.82]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.27, 0. , 0.7 ]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.03, 0. , 0.96]],
[[0. , 0. , 0. , 0. , 0. , 0.22, 0. , 0.07, 0. , 0.7 ]],
[[0. , 0. , 0. , 0. , 0. , 0.23, 0. , 0.01, 0. , 0.76]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.38, 0. , 0.59]],
[[0. , 0. , 0. , 0. , 0. , 0.07, 0. , 0.67, 0. , 0.25]],
[[0. , 0. , 0. , 0. , 0. , 0.17, 0. , 0.18, 0. , 0.65]],
[[0. , 0. , 0. , 0. , 0. , 0.19, 0. , 0.07, 0. , 0.74]],
[[0. , 0. , 0. , 0. , 0. , 0.43, 0. , 0.13, 0. , 0.44]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.81, 0. , 0.18]],
[[0. , 0. , 0. , 0. , 0. , 0.58, 0. , 0.18, 0. , 0.25]],
[[0. , 0. , 0. , 0. , 0. , 0.25, 0. , 0.56, 0. , 0.19]],
[[0. , 0. , 0. , 0. , 0. , 0.52, 0. , 0.08, 0. , 0.39]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.04, 0. , 0.95]],
[[0. , 0. , 0. , 0. , 0. , 0.27, 0. , 0.11, 0. , 0.61]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0. , 0. , 0.99]],
[[0. , 0. , 0. , 0. , 0. , 0.28, 0. , 0.68, 0. , 0.04]],
[[0. , 0. , 0. , 0. , 0. , 0.12, 0. , 0.38, 0. , 0.49]],
[[0. , 0. , 0. , 0. , 0. , 0.05, 0. , 0. , 0. , 0.95]],
[[0. , 0. , 0. , 0. , 0. , 0.27, 0. , 0.01, 0. , 0.72]],
[[0. , 0. , 0. , 0. , 0. , 0.08, 0. , 0.39, 0. , 0.53]],
[[0. , 0. , 0. , 0. , 0. , 0.64, 0. , 0.12, 0. , 0.24]],
[[0. , 0. , 0. , 0. , 0. , 0.1 , 0. , 0.1 , 0. , 0.81]],
[[0. , 0. , 0. , 0. , 0. , 0.81, 0. , 0.03, 0. , 0.16]],
[[0. , 0. , 0. , 0. , 0. , 0.06, 0. , 0.06, 0. , 0.88]],
[[0. , 0. , 0. , 0. , 0. , 0.06, 0. , 0.78, 0. , 0.16]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.01, 0. , 0.98]],
[[0. , 0. , 0. , 0. , 0. , 0.67, 0. , 0.32, 0. , 0.01]],
[[0. , 0. , 0. , 0. , 0. , 0.1 , 0. , 0.86, 0. , 0.04]],
[[0. , 0. , 0. , 0. , 0. , 0.19, 0. , 0.01, 0. , 0.8 ]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.25, 0. , 0.74]],
[[0. , 0. , 0. , 0. , 0. , 0.91, 0. , 0.05, 0. , 0.05]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.47, 0. , 0.51]],
[[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.13, 0. , 0.87]],
[[0. , 0. , 0. , 0. , 0. , 0.04, 0. , 0.62, 0. , 0.35]],
[[0. , 0. , 0. , 0. , 0. , 0.02, 0. , 0.66, 0. , 0.32]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.04, 0. , 0.95]],
[[0. , 0. , 0. , 0. , 0. , 0.25, 0. , 0.43, 0. , 0.32]],
[[0. , 0. , 0. , 0. , 0. , 0.37, 0. , 0.13, 0. , 0.5 ]],
[[0. , 0. , 0. , 0. , 0. , 0.74, 0. , 0.11, 0. , 0.15]],
[[0. , 0. , 0. , 0. , 0. , 0.37, 0. , 0.36, 0. , 0.27]],
[[0. , 0. , 0. , 0. , 0. , 0.07, 0. , 0.09, 0. , 0.84]],
[[0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.85, 0. , 0.15]],
[[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.21, 0. , 0.79]],
[[0. , 0. , 0. , 0. , 0. , 0.7 , 0. , 0. , 0. , 0.29]],
[[0. , 0. , 0. , 0. , 0. , 0.22, 0. , 0.05, 0. , 0.73]],
[[0. , 0. , 0. , 0. , 0. , 0.55, 0. , 0.32, 0. , 0.14]],
[[0. , 0. , 0. , 0. , 0. , 0.21, 0. , 0.09, 0. , 0.7 ]]],
dtype=float32)
'''
np.round(y_proba[:1], 2)
'''
array([[0. , 0. , 0. , 0. , 0. , 0.21, 0. , 0.27, 0. , 0.51]],
dtype=float32)
'''
y_std = y_probas.std(axis=0)
np.round(y_std[:1], 2)
'''
array([[0. , 0. , 0. , 0. , 0. , 0.24, 0. , 0.28, 0. , 0.31]],
dtype=float32)
'''
y_pred = np.argmax(y_proba, axis=1)
accuracy = np.sum(y_pred == y_test) / len(y_test)
accuracy # 0.8614
class MCDropout(keras.layers.Dropout):
def call(self, inputs):
return super().call(inputs, training=True)
class MCAlphaDropout(keras.layers.AlphaDropout):
def call(self, inputs):
return super().call(inputs, training=True)
tf.random.set_seed(42)
np.random.seed(42)
mc_model = keras.models.Sequential([
MCAlphaDropout(layer.rate) if isinstance(layer, keras.layers.AlphaDropout) else layer for layer in model.layers
])
mc_model.summary()
'''
Model: "sequential_28"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_26 (Flatten) (None, 784) 0
_________________________________________________________________
mc_alpha_dropout (MCAlphaDro (None, 784) 0
_________________________________________________________________
dense_486 (Dense) (None, 300) 235500
_________________________________________________________________
mc_alpha_dropout_1 (MCAlphaD (None, 300) 0
_________________________________________________________________
dense_487 (Dense) (None, 100) 30100
_________________________________________________________________
dropout_5 (Dropout) (None, 100) 0
_________________________________________________________________
dense_488 (Dense) (None, 10) 1010
=================================================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0
_________________________________________________________________
'''
optimizer = keras.optimizers.SGD(learning_rate=0.01, momentum=0.9, nesterov=True)
mc_model.compile(loss='sparse_categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
mc_model.set_weights(model.get_weights())
np.round(np.mean([mc_model.predict(X_test_scaled[:1]) for sample in range(100)], axis=0), 2)
'''
array([[0. , 0. , 0. , 0. , 0. , 0.2 , 0. , 0.26, 0. , 0.54]],
dtype=float32)
'''
# 最大范数正则化
layer = keras.layers.Dense(100, activation='selu', kernel_initializer='lecun_normal', kernel_constraint=keras.constraints.max_norm(1.))
MaxNormDense = partial(keras.layers.Dense, activation='selu', kernel_initializer='lecun_normal',
kernel_constraint=keras.constraints.max_norm(1.))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
MaxNormDense(300),
MaxNormDense(100),
keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy', optimizer='nadam', metrics=['accuracy'])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, validation_data=(X_valid_scaled, y_valid))
