3-训练模型

理论部分

线性回归

• 线性回顾模型预测

\[\hat y = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n \]

\[其中，\hat y是预测值；n是特征数量；x_i是第i个特征值；\theta_j是第j个模型参数 \]

\[向量化形式：\hat y = h_\theta(x)=\theta·x \]

• 线性回归的MSE成本函数

\[MSE = (X, h_\theta)=\frac{1}{m}\sum^m_{i=1}(\theta^Tx^{(i)}-y^{(i)})^2 \]

• 标准方程
  • 为了得到使成本函数最小的θ值，有一个闭式解方法，也就是一个直接得出结果的数学方程，及标准方程

\[\hat \theta = (X^TX)^{-1}X^Ty \]

\[\hat \theta是使成本函数最小的\theta值；y是包含y^{(1)}到y^{(m)}的目标值向量 \]

• 利用伪逆计算

\[\hat \theta = X^+y，其中 X^+是X的伪逆 \]

伪逆本身是使用被称为奇异值分解(SVD)的标准矩阵分解技术来计算的，可以将训练集矩阵X分解为三个矩阵UΣV^T的乘积。伪逆的计算公式为X⁺=VΣ⁺U^T。为了计算矩阵Σ⁺，该算法取Σ并将所有小于一个小阈值的值设置为0，然后将所有非零值替换成它们的倒数，最后把结果矩阵转置。这种方法比计算标准方程更有效，再加上它可以很好地处理边缘情况：的确，如果矩阵X^TX是不可逆的(即奇异的)，标准方程可能没有解，例如m<n或某些特征是多余的，但伪逆总是有定义的。

• 梯度下降

  • 批量梯度下降
  • 随机梯度下降
  • 小批量梯度下降
  \[成本函数的偏导数：\frac{\partial}{\partial\theta_j}MSE(\theta)=\frac{2}{m}\sum^m_{i=1}(\theta^Tx^{(i)}-y^{(i)})x^{(i)}_j \]

\[成本函数的梯度向量：\nabla_\theta MSE(\theta)=\begin{vmatrix} \frac{\partial}{\partial\theta_0}MSE(\theta) \\ \frac{\partial}{\partial\theta_1}MSE(\theta) \\ ... \\ \frac{\partial}{\partial\theta_n}MSE(\theta) \end{vmatrix}=\frac{2}{m}X^T(X\theta-y) \]

\[\theta^{下一步}=\theta - \eta\nabla_\theta MSE(\theta) \]

多项式回归

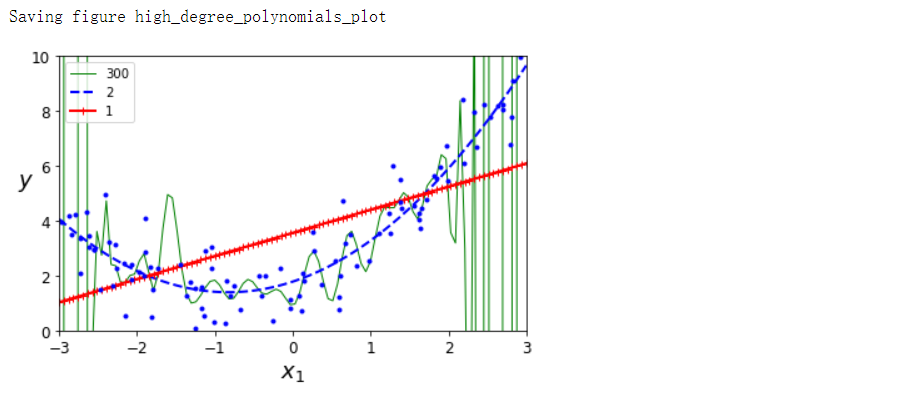
• 当存在多个特征时，多项式回归能够找到特征之间的关系(这是普通线性回归模型无法做到的)

• 学习曲线

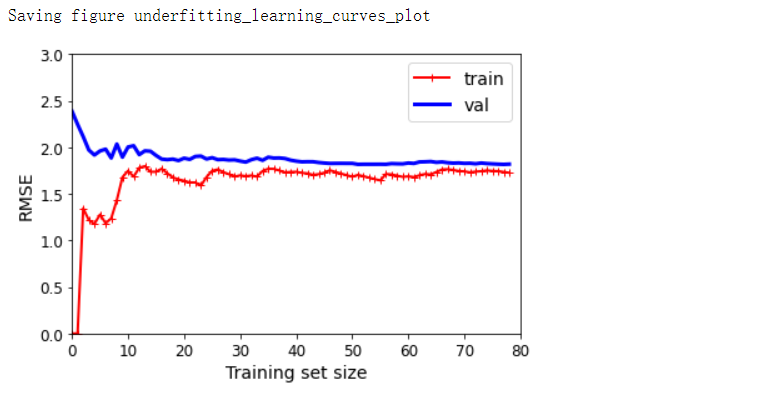
  • 一种区别模型是否过于简单或过于复杂的方法
  • 典型的欠拟合模型：两条曲线都达到了平稳状态，它们很接近而且很高
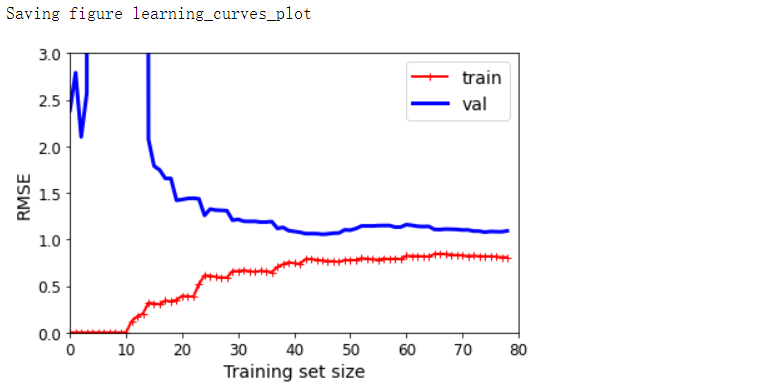
  • 曲线之间存在间隙。这意味着该模型在训练数据上的性能要比在验证数据上的性能好得多，这是过拟合模型的标志

偏差/方差权衡

• 统计学和机器学习的重要理论成果是以下事实：模型的泛化误差可以表示为三个非常不同的误差之和
  • 偏差
    • 这部分泛化误差的原因在于错误的假设，比如假设数据是线性的，而实际上是二次的。高偏差模型最有可能欠拟合训练数据
  • 方差
    • 这部分是由于模型对训练数据的细微变化过于敏感。具有许多自由度的模型(例如高阶多项式模型)可能具有较高的方差，因此可能过拟合训练数据
  • 不可避免的误差
    • 这部分误差是因为数据本身的噪声所致。减少这部分误差的唯一方法就是清理数据
  • 增加模型的复杂度通常会显著提升模型的防擦并减少偏差。反过来，降低模型的复杂度则会提升模型的偏差并降低方差。这就是为什么称其为权衡。

正则化线性模型

• 对于线性模型，正则化通常是通过约束模型的权重来实现的

• 岭回归

  • \[岭回归成本函数：J(\theta)=MSE(\theta)+\alpha\frac{1}{2}\sum^n_{i=1}\theta^2_i \]

  • \[闭式解的岭回归：\hat \theta=(X^T+\alpha A)^{-1}X^Ty \]

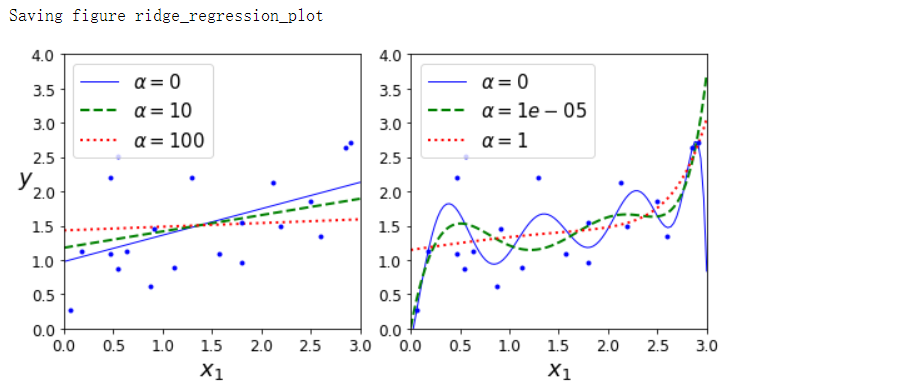
  • 在执行岭回归之前缩放数据很重要，因为它对输入特征的缩放敏感

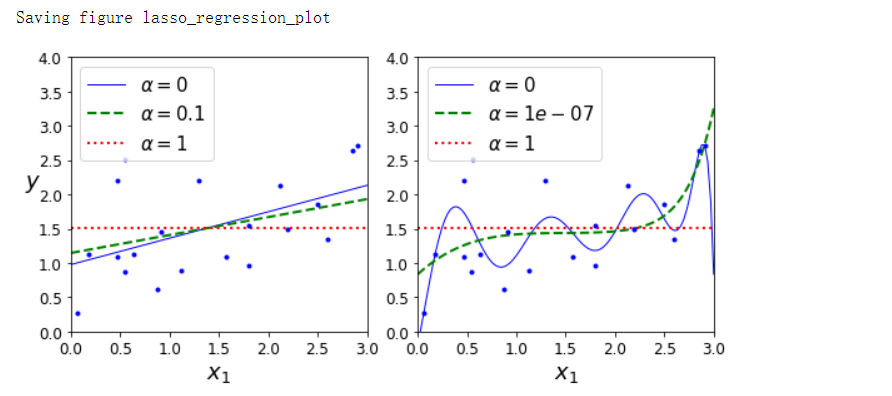
• Lasso回归

  • 线性回归的另一种正则化叫作最小绝对收缩和选择算子回归

  • \[Lasso回归成本函数：J(\theta)=MSE(\theta)+\alpha \sum^n_{i=1}|\theta_i| \]

  • Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重(也就是将它们设置为0)，换句话说，Lasso回归会自动执行特征选择并输出一个稀疏模型

  • \[Lasso回归子梯度向量：g(\theta, J)=\nabla_\theta MSE(\theta)+\alpha \begin{vmatrix} sign(\theta_1) \\ sign(\theta_2) \\ ... sign(\theta_n) \\ \end{vmatrix}，其中sign(\theta_i)=\left\{ \begin{aligned} -1， 如果\theta_i<0 \\ 0，如果\theta=0 \\ +1，如果\theta>0 \end{aligned} \right . \]

• 弹性网络

  • 弹性网络是介于岭回归和Lasso回归之间的中间地带，大多数情况下，你应该避免使用纯线性回归。岭回归是个不错的默认选择，但是如果你觉得实际用到的特征只有少数几个，那就应该更倾向于Lasso回归或是弹性网络，因为它们会将无用特征的权重降为0.一般而言，弹性网络优于Lasso回归，因为当特征数量超过训练实例数量，又或是几个特征强相关时，Lasso回归的表现可能非常不稳定

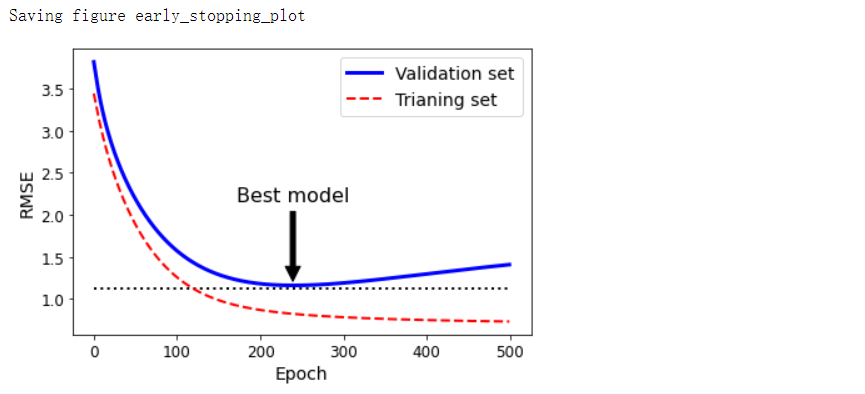
提前停止法

• 对于梯度下降这一类迭代学习的算法，还有一个与众不同的正则化方法，就是在验证误差达到最小值时停止训练，该方法叫作提前停止法。
• 经过一轮一轮的训练，算法不断地学习，训练集上的预测误差(RMSE)自然不断下降，同样其在验证集上的预测误差也随之下降。但是一段时间之后，验证误差停止下降反而开始回升，这说明模型开始过拟合训练数据，通过早期停止法，一旦验证误差达到最小值，就立刻停止训练，这是一个非常简单而有效的正则化技巧，所以称为“美丽的免费午餐”

逻辑回归

• 逻辑回归被广泛用于估算一个实例属于某个特定类别的概率。
• 逻辑回归模型也是计算输入特征的加权和(加上偏置项)，但是不同于线性回归模型直接输出结果，它输出的是结果的数理逻辑值

\[逻辑回归模型的估计概率：\hat p = h_\theta(x)=\sigma(x^T\theta) \]

\[逻辑记为\sigma(·)，是一个sigmoid函数，逻辑函数：\sigma(t)=\frac{1}{1+exp(-t)} \]

\[逻辑回归模型预测：\hat y=\left\{ \begin{matrix} 0，如果\hat p<0.5， \\ 1，如果\hat p>=0.5 \end{matrix} \right . \]

分数t通常称为logit。该名称源于以下事实：定义为logit(p)=log(p/(1-p))的logit函数与logistic函数相反。确实，如果你计算估计概率p的对数，则会发现结果为t。对数也称为对数奇数，因为它是正类别的估计概率与负类别的估计概率之比的对数

\[单个训练实例的成本函数：c(\theta)=\left\{ \begin{matrix} -log(\hat p)，如果y=1 \\ -log(1-\hat p)，如果y=0 \end{matrix} \right . \]

\[逻辑回归成本函数(对数损失、交叉熵损失函数)：J(\theta)=-\frac{1}{m}\sum^m_{i=1}[y^{(i)}log(\hat p ^{(i)})+(1-y^{(i)}log(1-\hat p^{(i)}))] \]

\[逻辑成本函数偏导数：\frac{\partial}{\partial \theta_j}J(\theta)=\frac{1}{m}\sum^m_{i=1}(\sigma(\theta^Tx^{(i)})-y^{(i)})x_j^{(i)} \]

Softmax回归

• 逻辑回归模型经过推广，可以直接支持多个类别，而不需要训练并且组合多个二元分类器，这就是Softmax回归，或者叫作多元逻辑回归
• 原理：给定一个实例x，Softmax回归模型首先计算出每个类k的分数s_k(x)，然后对这些分数应用Softmax函数(也叫归一化函数)，估算出每个类的概率。

\[类k的Softmax分数：s_k(x)=x^T\theta^{(k)} \]

\[请注意，每个类都有自己的特定参数向量\theta^{(k)}，所有这些向量通常都作为行存储在参数矩阵\Theta中 \]

\[softmax函数计算每个分数的指数，然后对其进行归一化。分数通常称为对数或对数奇数，尽管它们实际上是未归一化的对数奇数 \\ \hat p_k = \sigma(s(x))_k=\frac{exp(s_k(x))}{\sum ^K_{j=1}exp(s_j(x))} \\ 此等式中：K是类数；s(x)是一个向量，其中包含实例x的每个类的分数；\sigma(s(x))_k是实例x属于k的估计概率，给定该实例每个类的分数 \]

\[Softmax回归分类预测：\hat y = {\underset {k} argmax}\sigma(s(x))_k={\underset {k}argmaxs_k(x)}={\underset {k}argmax}((\theta^{(k)})^Tx) \]

• 交叉熵成本函数
  • 交叉熵通常被用来衡量一组估算出的类概率跟目标类的匹配程度
  • 交叉熵源于信息理论，假设你想要有效传递每天的天气信息，交叉熵测量的是你每次发送天气选项的平均比特数。如果你对天气的假设是完美的，交叉熵将会等于天气本身的熵(也就是其本身固有的不可预测性)。但是如果你的假设是错误的(比如经常下雨)，交叉熵将会变大，增加的这一部分我们称之为KL散度(也叫相对熵)

\[交叉熵成本函数：J(\Theta)=-\frac{1}{m}\sum^m_{i=1}\sum^K_{k=1}y^{(i)}_klog(\hat p_k^{(i)}) \\ y^{(i)}_k是属于类k的第i个实例的目标概率，一般而言等于1或0，具体取决于实例是否属于该类 \]

\[类k的交叉熵梯度向量：\nabla_{\theta(k)}J(\Theta)=\frac{1}{m}\sum^m_{i=1}(\hat p^{(i)}_k-y^{(i)}_k)x^{(i)} \]

代码部分

引入

import sys
assert sys.version_info >= (3, 5)

import sklearn
assert sklearn.__version__ >= '0.20'

import numpy as np
import os

np.random.seed(42)

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

PROJECT_ROOT_DIR = '.'
CHAPTER_ID = 'training_linear_models'
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, 'images', CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)

def save_fig(fig_id, tight_layout=True, fig_extension='png', resolution=300):
    path = os.path.join(IMAGES_PATH, fig_id + '.' + fig_extension)
    print('Saving figure', fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path, format=fig_extension, dpi=resolution)

使用正规方程求解线性回归（最小二乘法）

import numpy as np

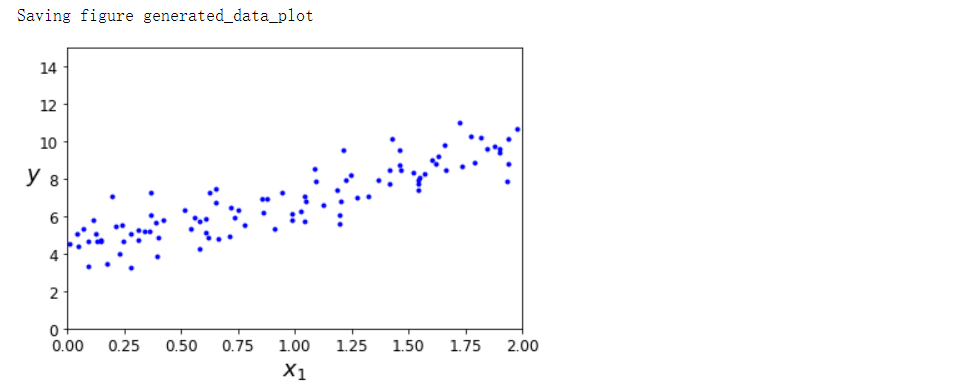
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
plt.plot(X, y, 'b.')
plt.xlabel('$x_1$', fontsize=18)  # 下标1
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
save_fig('generated_data_plot')
plt.show()

X_b = np.c_[np.ones((100, 1)), X]  # add x0 = 1 to each instance，为了添加偏置项，theta0
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best  # array([[4.21509616], [2.77011339]])

X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
y_predict = X_new_b.dot(theta_best)
y_predict  # array([[4.21509616], [9.75532293]])

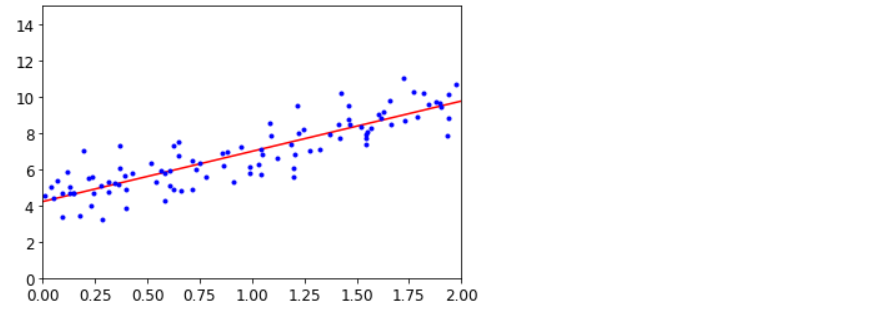
plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

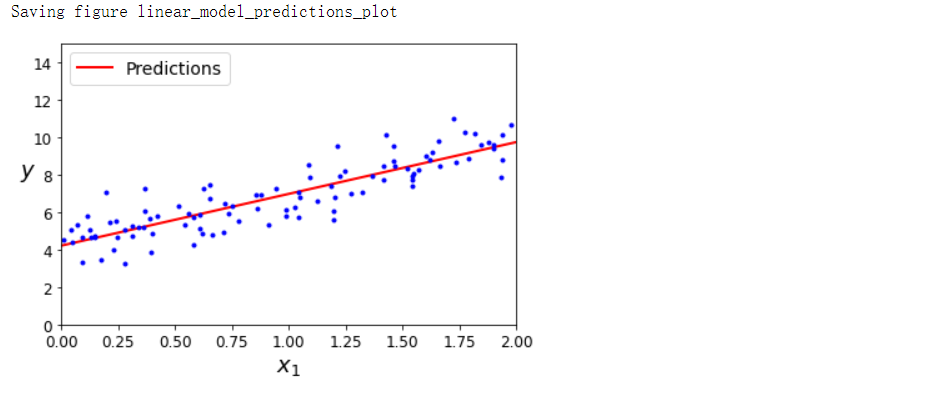
plt.plot(X_new, y_predict, 'r-', linewidth=2, label='Predictions')
plt.plot(X, y, 'b.')
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.legend(loc='upper left', fontsize=14)
plt.axis([0, 2, 0, 15])
save_fig('linear_model_predictions_plot')
plt.show()

• 直接调用sklearn

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_  # (array([3.56401543]), array([[0.84362064]]))

lin_reg.predict(X_new)  # array([[4.21509616], [9.75532293]])

• 调用scipy

# 线性回归类基于scipy. linalgl .lstsq()函数(名称代表“最小二乘”)，可以直接调用
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd  # array([[4.21509616], [2.77011339]])

• 伪逆

np.linalg.pinv(X_b).dot(y)  # array([[4.21509616], [2.77011339]])

批量梯度下降求解线性回归

eta = 0.1  # 学习率
n_iterations = 1000  # 迭代次数
m = 100
theta = np.random.randn(2, 1)  # 随机初始化
for iteration in range(n_iterations):
    gradients = 2/m * X_b.T.dot(X_b.dot(theta) -y)
    theta = theta - eta * gradients

theta  # array([[4.21509616], [2.77011339]])

X_new_b.dot(theta)  # array([[4.21509616], [9.75532293]])

theta_path_bgd = []

def plot_gradient_descent(theta, eta, theta_path=None):
    m = len(X_b)
    plt.plot(X, y, 'b.')
    n_iterations = 1000
    for iteration in range(n_iterations):
        if iteration < 10:
            y_predict = X_new_b.dot(theta)
            style = 'b-' if iteration > 0 else 'r--'
            plt.plot(X_new, y_predict, style)
        gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
        theta = theta - eta * gradients
        if theta_path is not None:
            theta_path.append(theta)
    plt.xlabel('$x_1$', fontsize=18)
    plt.axis([0, 2, 0, 15])
    plt.title(r'$\eta = {}$'.format(eta), fontsize=16)

np.random.seed(42)
theta = np.random.randn(2, 1)  # 随机初始化
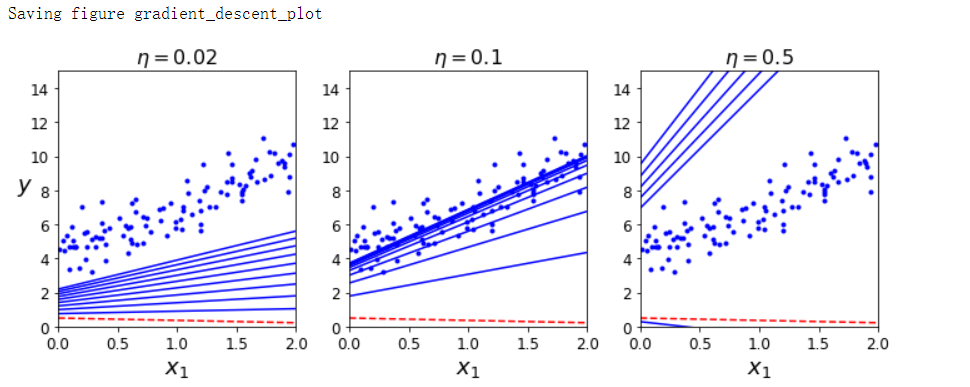
plt.figure(figsize=(10, 4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
save_fig('gradient_descent_plot')
plt.show()

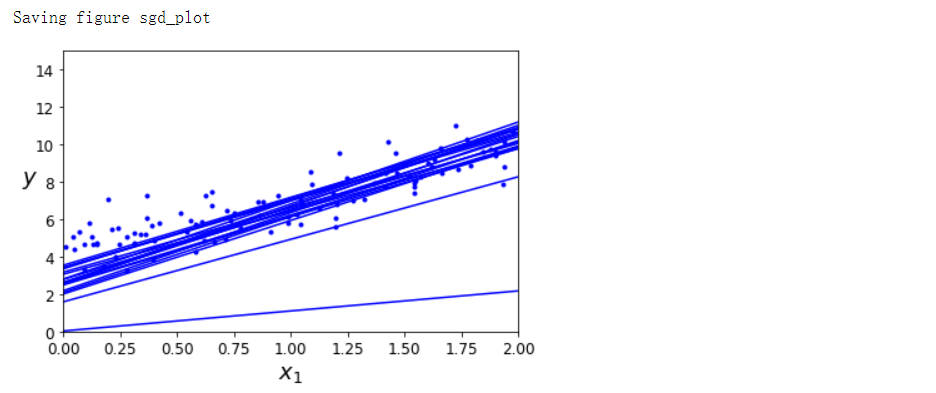
随机梯度下降

theta_path_sgd = []
m = len(X_b)
np.random.seed(42)
n_epochs = 50  # 迭代轮数
t0, t1 = 5, 50  # 学习计划超参数
def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2, 1)  # 随机初始化

for epoch in range(n_epochs):
    for i in range(m):
        if epoch == 0 and i < 20:
            y_predict = X_new_b.dot(theta)
            style = 'b-' if i > 0 else 'r--'
            plt.plot(X_new, y_predict, style)
        random_index = np.random.randint(m)  # 随机选择一个数据做梯度下降
        xi = X_b[random_index: random_index+1]
        yi = y[random_index: random_index+1]
        gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(epoch * m + i)  # 越到后面，学习率越小
        theta = theta - eta * gradients
        theta_path_sgd.append(theta)
    
plt.plot(X, y, 'b.')
plt.xlabel('$x_1$', fontsize=18)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
save_fig('sgd_plot')
plt.show()

theta  # array([[4.20727007], [2.7427877 ]])

• 直接调用sklearn

# sklearn只有随机梯度下降
from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y.ravel())  # 扁平化

sgd_reg.intercept_, sgd_reg.coef_  # (array([4.24365286]), array([2.8250878]))

小批量梯度下降

theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2, 1)  # 随机初始化
t0, t1 = 200, 1000
def learning_schedule(t):
    return t0 / (t + t1)

t = 0
for epoch in range(n_iterations):
    shuffled_indices = np.random.permutation(m)  # 打散数据
    X_b_shuffled = X_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for i in range(0, m, minibatch_size):
        t += 1
        xi = X_b_shuffled[i: i+minibatch_size]
        yi = y_shuffled[i: i+minibatch_size]
        gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
        eta = learning_schedule(t)
        theta = theta - eta * gradients
        theta_path_mgd.append(theta)

theta  # array([[4.25214635], [2.7896408 ]])

theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(7, 4))
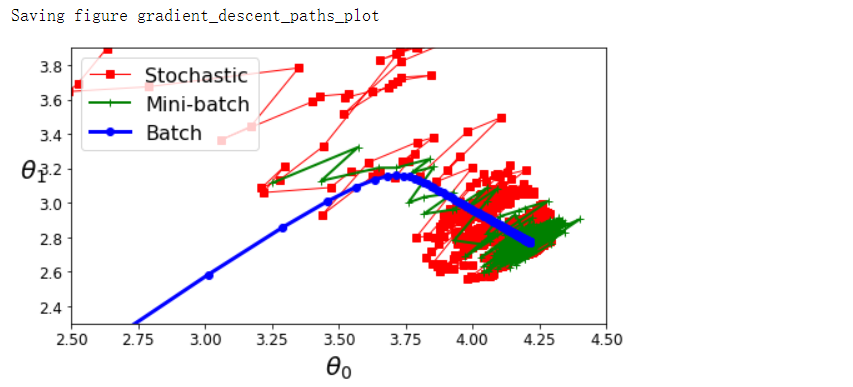
plt.plot(theta_path_sgd[:, 0], theta_path_sgd[:, 1], 'r-s', linewidth=1, label='Stochastic')
plt.plot(theta_path_mgd[:, 0], theta_path_mgd[:, 1], 'g-+', linewidth=2, label='Mini-batch')
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], 'b-o', linewidth=3, label='Batch')
plt.legend(loc='upper left', fontsize=16)
plt.xlabel(r'$\theta_0$', fontsize=20)
plt.ylabel(r'$\theta_1$', fontsize=20, rotation=0)
plt.axis([2.5, 4.5, 2.3, 3.9])
save_fig('gradient_descent_paths_plot')
plt.show()

多项式回归

import numpy as np
import numpy.random as rnd

np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
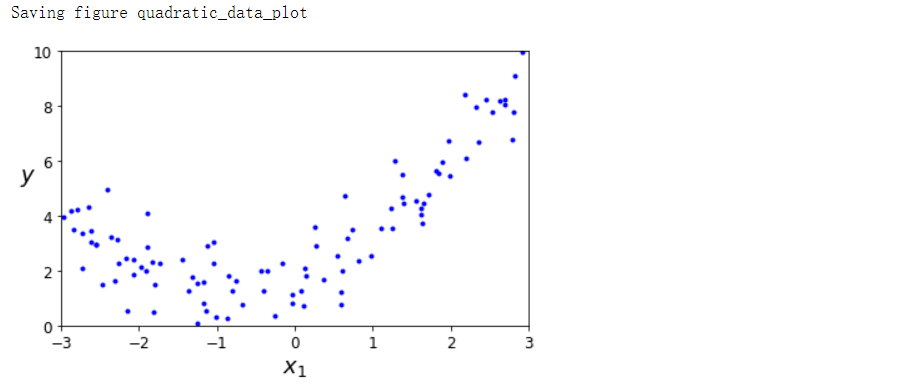
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, 'b.')
plt.xlabel('$x_1$', fontsize=18)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig('quadratic_data_plot')
plt.show()

from sklearn.preprocessing import PolynomialFeatures

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]  # array([-0.75275929])

X_poly[0]  # array([-0.75275929,  0.56664654])

lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_  # (array([1.78134581]), array([[0.93366893, 0.56456263]]))

X_new = np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
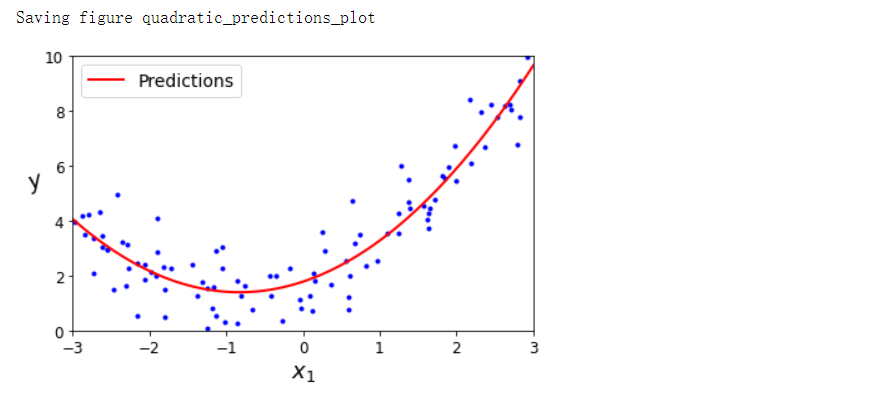
plt.plot(X, y, 'b.')
plt.plot(X_new, y_new, 'r-', linewidth=2, label='Predictions')
plt.xlabel('$x_1$', fontsize=18)
plt.ylabel('$y$', rotation=18, fontsize=18)
plt.legend(loc='upper left', fontsize=14)
plt.axis([-3, 3, 0, 10])
save_fig('quadratic_predictions_plot')
plt.show()

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

for style, width, degree in (('g-', 1, 300), ('b--', 2, 2), ('r-+', 2, 1)):
    polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
    std_scaler = StandardScaler()
    lin_reg = LinearRegression()
    polynomial_regression = Pipeline([
        ('poly_features', polybig_features),
        ('std_scaler', std_scaler),
        ('lin_reg', lin_reg),
    ])
    polynomial_regression.fit(X, y)
    y_newbig = polynomial_regression.predict(X_new)
    plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)

plt.plot(X, y, 'b.', linewidth=3)
plt.legend(loc='upper left')
plt.xlabel('$x_1$', fontsize=18)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig('high_degree_polynomials_plot')
plt.show()

学习曲线

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

def plot_learning_curves(model, X, y):
    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
    train_errors, val_errors = [], []
    for m in range(1, len(X_train)):
        model.fit(X_train[:m], y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
        val_errors.append(mean_squared_error(y_val, y_val_predict))
    plt.plot(np.sqrt(train_errors), 'r-+', linewidth=2, label='train')
    plt.plot(np.sqrt(val_errors), 'b-', linewidth=3, label='val')
    plt.legend(loc='upper right', fontsize=14)
    plt.xlabel('Training set size', fontsize=14)
    plt.ylabel('RMSE', fontsize=14)

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
plt.axis([0, 80, 0, 3])
save_fig('underfitting_learning_curves_plot')
plt.show()

from sklearn.pipeline import Pipeline

polynomial_regression = Pipeline([
    ('poly_features', PolynomialFeatures(degree=10, include_bias=False)),
    ('lin_reg', LinearRegression()),
])
plot_learning_curves(polynomial_regression, X, y)
plt.axis([0, 80, 0, 3])
save_fig('learning_curves_plot')
plt.show()

正则化

• 岭回归

np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)
from sklearn.linear_model import Ridge

ridge_reg = Ridge(alpha=1, solver='cholesky', rnadom_state=42)  # 正则化强度，正则化项系数
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])  # array([[1.55071465]])

ridge_reg = Ridge(alpha=1, solver='sag', random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])  # array([[1.5507201]])

from sklearn.linear_model import Ridge

def plot_model(model_class, polynomial, alphas, **model_kargs):
    for alpha, style in zip(alphas, ('b-', 'g--', 'r:')):
        model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
        if polynomial:
            model = Pipeline([
                ('poly_features', PolynomialFeatures(degree=10, include_bias=False)),
                ('std_scaler', StandardScaler()),
                ('regul_reg', model),
            ])
        model.fit(X, y)
        y_new_regul = model.predict(X_new)
        lw = 2 if alpha > 0 else 1
        plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r'$\alpha={}$'.format(alpha))
    plt.plot(X, y, 'b.', linewidth=3)
    plt.legend(loc='upper left', fontsize=15)
    plt.xlabel('$x_1$', fontsize=18)
    plt.axis([0, 3, 0, 4])
plt.figure(figsize=(8, 4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
save_fig('ridge_regression_plot')
plt.show()

sgd_reg = SGDRegressor(penalty='l2', max_iter=1000, tol=1e-3, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])  # array([1.47012588])

• Lasso回归

from sklearn.linear_model import Lasso

plt.figure(figsize=(8, 4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel('$y$', rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)
save_fig('lasso_regression_plot')
plt.show()

from sklearn.linear_model import Lasso

lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])  # array([1.53788174])

• 弹性网络回归

from sklearn.linear_model import ElasticNet

elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])  # array([1.54333232])

提前结束迭代，选择最优模型

np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)
X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(), test_size=0.5, random_state=10)
from copy import deepcopy

poly_scaler = Pipeline([
    ('poly_features', PolynomialFeatures(degree=90, include_bias=False)),
    ('std_scaler', StandardScaler()),
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, penalty=None, 
                       learning_rate='constant', eta0=0.0005, random_state=42)  # 用上一轮的结果作为本轮的初始化
minimum_val_error = float('inf')
best_epoch = None
best_model = None
for epoch in range(1000):
    sgd_reg.fit(X_train_poly_scaled, y_train)
    y_val_predict = sgd_reg.predict(X_val_poly_scaled)
    val_error = mean_squared_error(y_val, y_val_predict)
    if val_error < minimum_val_error:
        minimum_val_error = val_error
        best_epoch = epoch
        best_model = deepcopy(sgd_reg)

sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, penalty=None, 
                       learning_rate='constant', eta0=0.0005, random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
    sgd_reg.fit(X_train_poly_scaled, y_train)
    y_train_predict = sgd_reg.predict(X_train_poly_scaled)
    y_val_predict = sgd_reg.predict(X_val_poly_scaled)
    train_errors.append(mean_squared_error(y_train, y_train_predict))
    val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
plt.annotate('Best model',
             xy=(best_epoch, best_val_rmse),
             xytext=(best_epoch, best_val_rmse + 1),
             ha='center',
             arrowprops=dict(facecolor='black', shrink=0.05),
             fontsize=16,
            )
best_val_rmse -= 0.03  # 为了使图形看起来更方便
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], 'k:', linewidth=2)
plt.plot(np.sqrt(val_errors), 'b-', linewidth=3, label='Validation set')
plt.plot(np.sqrt(train_errors), 'r--', linewidth=2, label='Trianing set')
plt.legend(loc='upper right', fontsize=14)
plt.xlabel('Epoch', fontsize=14)
plt.ylabel('RMSE', fontsize=14)
save_fig('early_stopping_plot')
plt.show()

best_epoch, best_model
'''
(239, SGDRegressor(eta0=0.0005, learning_rate='constant', max_iter=1, penalty=None, random_state=42, tol=-inf, warm_start=True))
'''

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

t1a, t1b, t2a, t2b = -1, 3, -1.5, 1.5
t1s = np.linspace(t1a, t1b, 500)
t2s = np.linspace(t2a, t2b, 500)
t1, t2 = np.meshgrid(t1s, t2s)  # 网格化
T = np.c_[t1.ravel(), t2.ravel()]
Xr = np.array([[1, 1], [1, -1], [1, 0.5]])
yr = 2 * Xr[:, :1] + 0.5 * Xr[:, 1:]
J = (1/len(Xr) * np.sum((T.dot(Xr.T) - yr.T) ** 2, axis=1)).reshape(t1.shape)
N1 = np.linalg.norm(T, ord=1, axis=1).reshape(t1.shape)  # 求L1范数
N2 = np.linalg.norm(T, ord=2, axis=1).reshape(t1.shape)
t_min_idx = np.unravel_index(np.argmin(J), J.shape)
t1_min, t2_min = t1[t_min_idx], t2[t_min_idx]
t_init = np.array([[0.25], [-1]])

def bgd_path(theta, X, y, l1, l2, core=1, eta=0.05, n_iterations=200):
    path = [theta]
    for iteration in range(n_iterations):
        gradients = core * 2/len(X) * X.T.dot(X.dot(theta) - y) + l1 * np.sign(theta) + l2 * theta
        theta = theta - eta * gradients
        path.append(theta)
    return np.array(path)

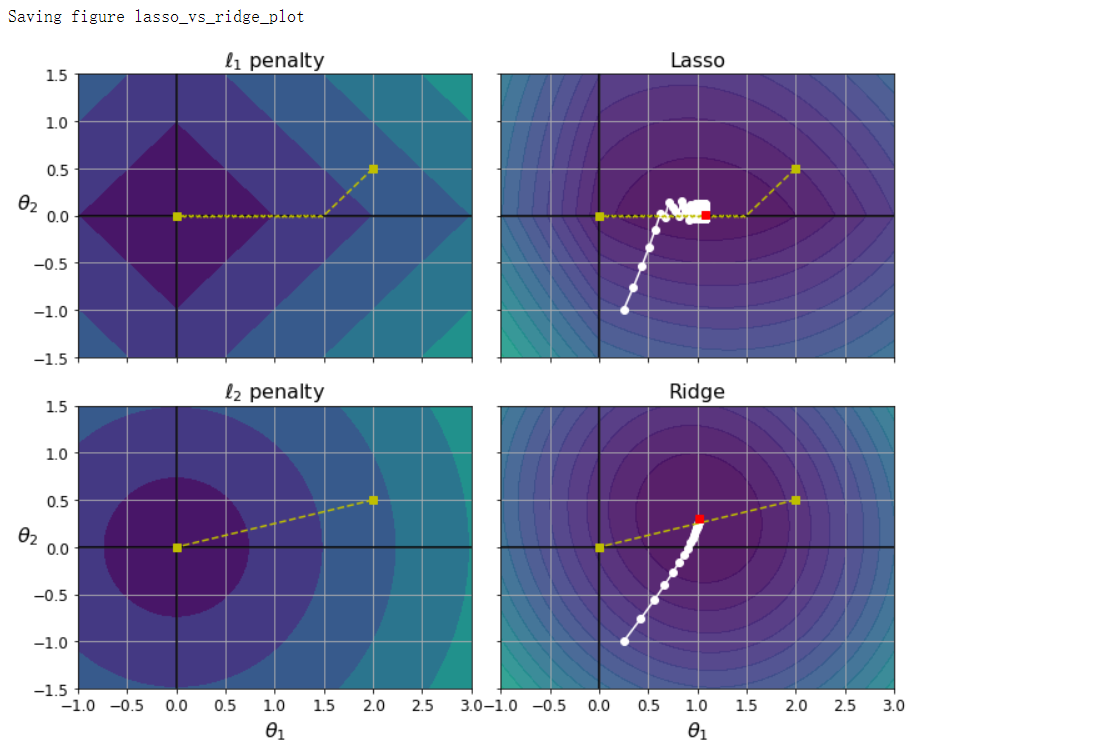
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10.1, 8))
for i, N, l1, l2, title in ((0, N1, 2.0, 0, 'Lasso'), (1, N2, 0.0, 2.0, 'Ridge')):
    JR = J + l1 * N1 + l2 * 0.5 * N2**2
    tr_min_idx = np.unravel_index(np.argmin(JR), JR.shape)
    t1r_min, t2r_min = t1[tr_min_idx], t2[tr_min_idx]
    levelsJ = (np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J)
    levelsJR = (np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR)
    levelsN = np.linspace(0, np.max(N), 10)
    path_J = bgd_path(t_init, Xr, yr, l1=0, l2=0)
    path_JR = bgd_path(t_init, Xr, yr, l1, l2)
    path_N = bgd_path(np.array([[2.0], [0.5]]), Xr, yr, np.sign(l1)/3, np.sign(l2), core=0)
    ax = axes[i, 0]
    ax.grid(True)
    ax.axhline(y=0, color='k')
    ax.axvline(x=0, color='k')
    ax.contourf(t1, t2, N/2.0, levels=levelsN)
    ax.plot(path_N[:, 0], path_N[:, 1], 'y--')
    ax.plot(0, 0, 'ys')
    ax.plot(t1_min, t2_min, 'ys')
    ax.set_title(r'$\ell_{}$ penalty'.format(i+1), fontsize=16)
    ax.axis([t1a, t1b, t2a, t2b])
    if i == 1:
        ax.set_xlabel(r'$\theta_1$', fontsize=16)
    ax.set_ylabel(r'$\theta_2$', fontsize=16, rotation=0)
    ax = axes[i, 1]
    ax.grid(True)
    ax.axhline(y=0, color='k')
    ax.axvline(x=0, color='k')
    ax.contourf(t1, t2, JR, levels=levelsJR, alpha=0.9)
    ax.plot(path_JR[:, 0], path_JR[:, 1], 'w-o')
    ax.plot(path_N[:, 0], path_N[:, 1], 'y--')
    ax.plot(0, 0, 'ys')
    ax.plot(t1_min, t2_min, 'ys')
    ax.plot(t1r_min, t2r_min, 'rs')
    ax.set_title(title, fontsize=16)
    ax.axis([t1a, t1b, t2a, t2b])
    if i == 1:
        ax.set_xlabel(r'$\theta_1$', fontsize=16)
save_fig('lasso_vs_ridge_plot')
plt.show()

逻辑回归

from sklearn import datasets
iris = datasets.load_iris()

import numpy as np
X = iris['data'][:, 3:]
y = (iris['target'] == 2).astype(np.int)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(solver='lbfgs', random_state=42)
log_reg.fit(X, y)

import matplotlib.pyplot as plt

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
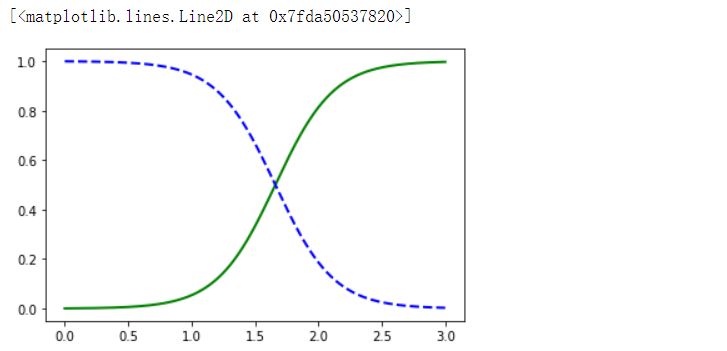
plt.plot(X_new, y_proba[:, 1], 'g-', linewidth=2, label='Iris virginica')
plt.plot(X_new, y_proba[:, 0], 'b--', linewidth=2, label='Not Iris virginica')

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
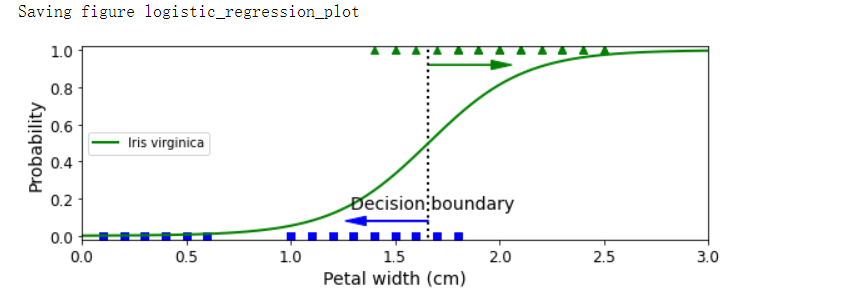
plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], 'bs')
plt.plot(X[y==1], y[y==1], 'g^')
plt.plot([decision_boundary, decision_boundary], [-1, 2], 'k:', linewidth=2)
plt.plot(X_new, y_proba[:, 1], 'g-', linewidth=2, label='Iris virginica')
plt.text(decision_boundary+0.02, 0.15, 'Decision boundary', fontsize=14, color='k', ha='center')
plt.arrow(decision_boundary, 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary, 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel('Petal width (cm)', fontsize=14)
plt.ylabel('Probability', fontsize=14)
plt.legend(loc='center left')
plt.axis([0, 3, -0.02, 1.02])
save_fig('logistic_regression_plot')
plt.show()

decision_boundary  # array([1.66066066])

log_reg.predict([[1.7], [1.5]])  # array([1, 0])

from sklearn.linear_model import LogisticRegression

X = iris['data'][:, (2, 3)]
y = (iris['target'] == 2).astype(np.int)
log_reg = LogisticRegression(solver='lbfgs', C=10**10, random_state=42)
log_reg.fit(X, y)
x0, x1 = np.meshgrid(
    np.linspace(2.9, 7, 500).reshape(-1, 1),
    np.linspace(0.8, 2.7, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = log_reg.predict_proba(X_new)
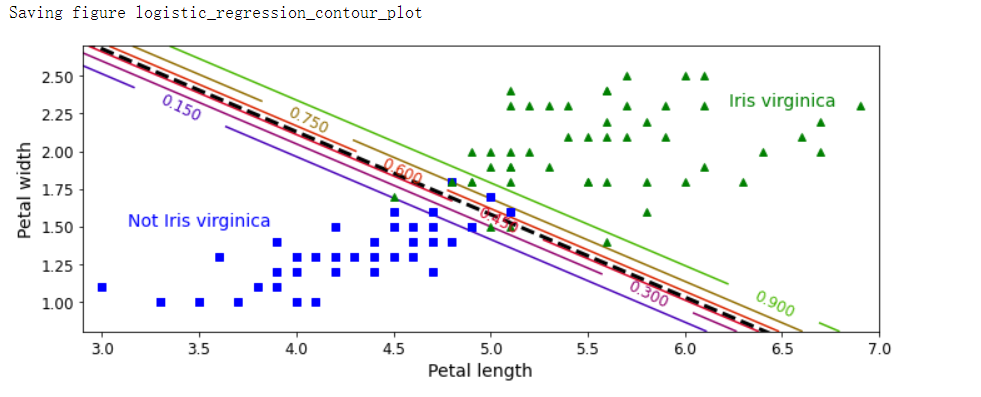
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], 'bs')
plt.plot(X[y==1, 0], X[y==1, 1], 'g^')
zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]
plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, 'k--', linewidth=3)
plt.text(3.5, 1.5, 'Not Iris virginica', fontsize=14, color='b', ha='center')
plt.text(6.5, 2.3, 'Iris virginica', fontsize=14, color='g', ha='center')
plt.xlabel('Petal length', fontsize=14)
plt.ylabel('Petal width', fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
save_fig('logistic_regression_contour_plot')
plt.show()

Softmax回归

X = iris['data'][:, (2, 3)]
y = iris['target']
softmax_reg = LogisticRegression(multi_class='multinomial', solver='lbfgs', C=10, random_state=42)
softmax_reg.fit(X, y)

x0, x1 = np.meshgrid(
    np.linspace(0, 8, 500).reshape(-1, 1),
    np.linspace(0, 3.5, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)
zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)
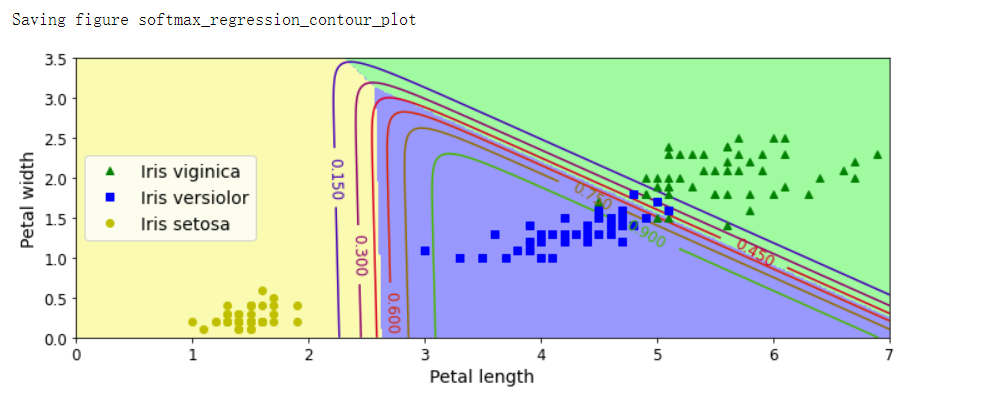
plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], 'g^', label='Iris viginica')
plt.plot(X[y==1, 0], X[y==1, 1], 'bs', label='Iris versiolor')
plt.plot(X[y==0, 0], X[y==0, 1], 'yo', label='Iris setosa')
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel('Petal length', fontsize=14)
plt.ylabel('Petal width', fontsize=14)
plt.legend(loc='center left', fontsize=14)
plt.axis([0, 7, 0, 3.5])
save_fig('softmax_regression_contour_plot')
plt.show()

softmax_reg.predict([[5, 2]])  # array([2])

softmax_reg.predict_proba([[5, 2]])  # array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])