Loading

13-AB Test学习

实验背景

Udacity的A/B Testing课程是由Google提供，重点是A/B测试的设计和分析。课程包括如何选择和定义衡量指标，如何设计一个具有统计功效(statistical power)的实验，以及如何分析结果并得出可靠的结论。

  • 实验策略
    • 在点击免费试用按钮后，对照组不会出现弹窗，直接进入免费试用课程的流程。实验组加了弹窗，需要用户回答他们每周有多少时间可以投入到课程中
    • 如果学生表示每周有5个小时或者更多的时间，他们将会像往常一样通过检查流程，如果他们表示每周不到5个小时，就会出现一条信息，说需要更多的时间投入才能成功完成课程，并表明学生可以免费获得课程材料
    • 无论如何，学生都可以选择继续参加免费试用课程或者免费获取课程材料
  • 策略目标
    • 实验假设了加入弹窗填时间这个步骤可以提醒用户了解到自己的学习时间是否足以完成课程。通过让部分用户察觉到自己学习时间不足以完成任务，从而自动放弃免费试用课程，最后可以提高整体用户的课程完成率，另一方面也可以为辅助老师减压，让他们专注于哪些可以投入更多时间的用户

指标选择

一个成功的A/B实验应该有两种类型的指标：

  • 第一类指标 invariant metrics
    • 原则上不能发生变化的指标，用来作为策略的健康检验，确保新上线的策略不会发生原则性错误。用来确保实验的变化确实是由策略造成的，就好比控制变量，在研究某一个自变量对因变量的影响时，需要控制其它变量一样
    • 对于每一个指标，都需要声明一个Dmin，它标志着最小的变化，这对业务来说是非常重要的。例如任何低于2%的转化率变化，即使在统计上是显著的，对企业来说也是不实际的
    • 第一类指标包括：uv独立访客数，用去重Cookies计数、免费试用按钮的点击量、点击率
指标 计算公式 Dmin 标识
uv unique daily cookies on page 3000 cookies Ck
clicks unique daily cookies who clicked 240 clicks Cl
CTP Cl/Ck 0.01 CTP
  • 第二类指标 evaluation metrics
    • 第二类指标是我们希望变化的指标，这个和实验的产品或者商业目标有关
      • 课程登记转化率(Gross Conversion):课程登记用户数/免费试用按钮点击量
      • 全流程转化率(Net Conversion):课程付费用户数/免费试用按钮点击量
指标 计算公式 Dmin 标识
Gross Conversion enrolled/Cl 0.01 ConversionGross
Net Conversion Paid/Cl 0.0075 ConversionNet

估计样本标准差

在开始实验之前，我们需要知道这些指标在策略上线之前的平时表现如何，即baseline values，基线值。这些数据应该是从日常数据中聚合得到的（日均）。

  • 基线数据
baseline = {
  "Cookies": 40000,
  "Clicks": 3200,
  "Enrollments": 600,
  "CTP": 0.08,
  "GConversion": 0.20625,
  "NConversion": 0.109313
}

  • 估计样本的标准差

    • 估计标准差(Standard Deviation)是后续计算实验样本量和置信区间的前提。同时，如果指标变化越大，获得置信结果就越难
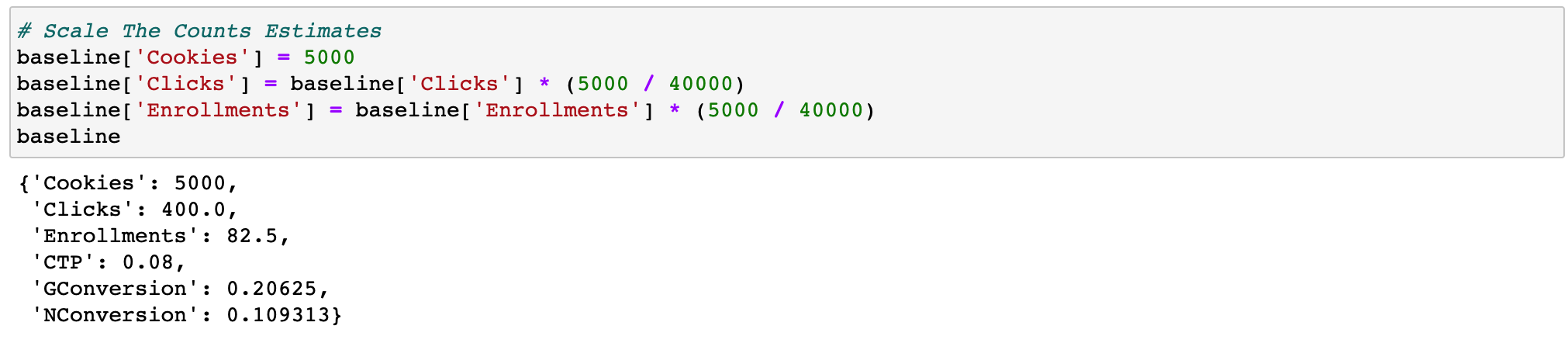
    • 缩放数据
      • 假设每天访问课程介绍页面的样本(cookies)大小为5000个，这里5000是项目给出的，作为用来估计标准差的抽样样本大小，我们希望基于5000这个数值，估计一个标准差，仅用于评估指标，这个样本量应该小于我们基线值(40000)
      • 因为我们用5000样本来估计标准差，所以其它的绝对量(点击量clicks，登记数enrollments)都应该进行等比的缩放，相对比值指标保持不变

  • 估计标准差

    • 假设转化率指标满足二项分布，就拿课程登记转化率(Gross Conversion)来说，课程登记用户数/免费试用按钮点击量，一次点击，要么登记课程，要么退回不登记课程，所以这个转化率对应二项分布中时间成功发生的概率p，那么总体方差为np(1-p)，由中心极限定理，从总体抽取一定样本，样本标准差的估计量为：

    \[SD=\sqrt{\frac{\hat p*(1-\hat p)}{n}} \]

    • 注意，并不是所有转化率(比例指标)的标准差估计都可以利用上述公式，这里需要区分两个概念
      • unit of diversion 分流单元
      • unit of analysis 分析单元(通常指指标的分母)
      • 分流单元被用来定义哪个用户或者触发哪个事件会进行样本分流(实验组和对照组)，它可以是一种独立标识，比如user_id或者cookie，也可以是一种基于事件的，比如page view(每当用户重新刷新页面时就会进行一次分流)。选择unit of diversion取决于以下三种重要的因素：
        • 用户一致性(User consistency)：如果我们上线的策略对用户是可见的(例如UI类实验，改下button颜色啥的)，原则是让用户始终有一致的体验。因此，选择User_ID或Cookie作为分流单元是不错的选择。如果我们上线的策略对用户是不可见的，那么基于事件的分流，如页面浏览将更有意义。
        • 理论考量(Ethical considerations)
        • 指标变化性(Variability of metrics)：指标变化性越大，代表样本指标值之间的波动会比较大，如果分流单元比分析单元的范围更大，则指标的变化性要高得多。分析单元一般是指指标的分母，例如对于点击率(CTP=click/PV)，PV称为分析单元。因此，如果使用user_id作为分流单元，以PV作为分析单元，CTP的变化性就回变高，因为一个user_id可以对应对个PV。只有当实验的分流单元等于分析单元的时候，才满足上述样本标准差估计量的计算方法，如果不满足条件，则可以依据经验给定。
# 估计两种转化率的标准差
conversion_dict = {
    'GConversion': [0.01, 'Clicks'],
    'NConversion': [0.0075, 'Clicks']
}

def cal_sd(conversion, d_min, denominator):
    '''
    Conversion:转化率名称
    d_min:最小变化
    denominator:转化率的分母
    '''
    R = {}
    R['d_min'] = d_min
    R['p'] = baseline[conversion]
    R['n'] = baseline[denominator]
    R['sd'] = round(math.sqrt((R['p'] * (1 - R['p'])) / R['n']), 4)
    print('{} 标准差'.format(conversion), R['sd'])

conversions = ['GConversion', 'NConversion']
for conversion in conversions:
    d_min = conversion_dict[conversion][0]
    denominator = conversion_dict[conversion][1]
    cal_sd(conversion, d_min, denominator)
# GConversion 标准差 0.0202
# NConversion 标准差 0.0156

计算实验样本量

  • 一旦估计出小流量实验(样本)的指标标准差，就可以计算出实验所需的样本量，太多了会浪费很多资源，太少了会因为统计灵敏度太低而得不到显著的结论。在计算样本量之前，必须弄懂假设检验中的两个概念：
    • (1)第一类错误α：当原假设为真的时候，却拒绝的概率，拒真错误，也被称为Significance Level(显著性水平)。对于A/B测试，犯这个错误代表新策略没有收益，但是却认为有收益，然后上线的错误
    • (2)第二类错误β：当原假设为假的时候(备择假设为真)，却接受原假设的概率，纳伪错误。而Statistical Power(统计功效)=1-β。直观上理解，AB两组即使有差异，也不一定被你观测出来，必须保证一定的条件(比如样本要充足)才能使你观测出统计量之间的差异，而统计功效就是当AB两组实际有差异时，能被我们检测出来差异的概率
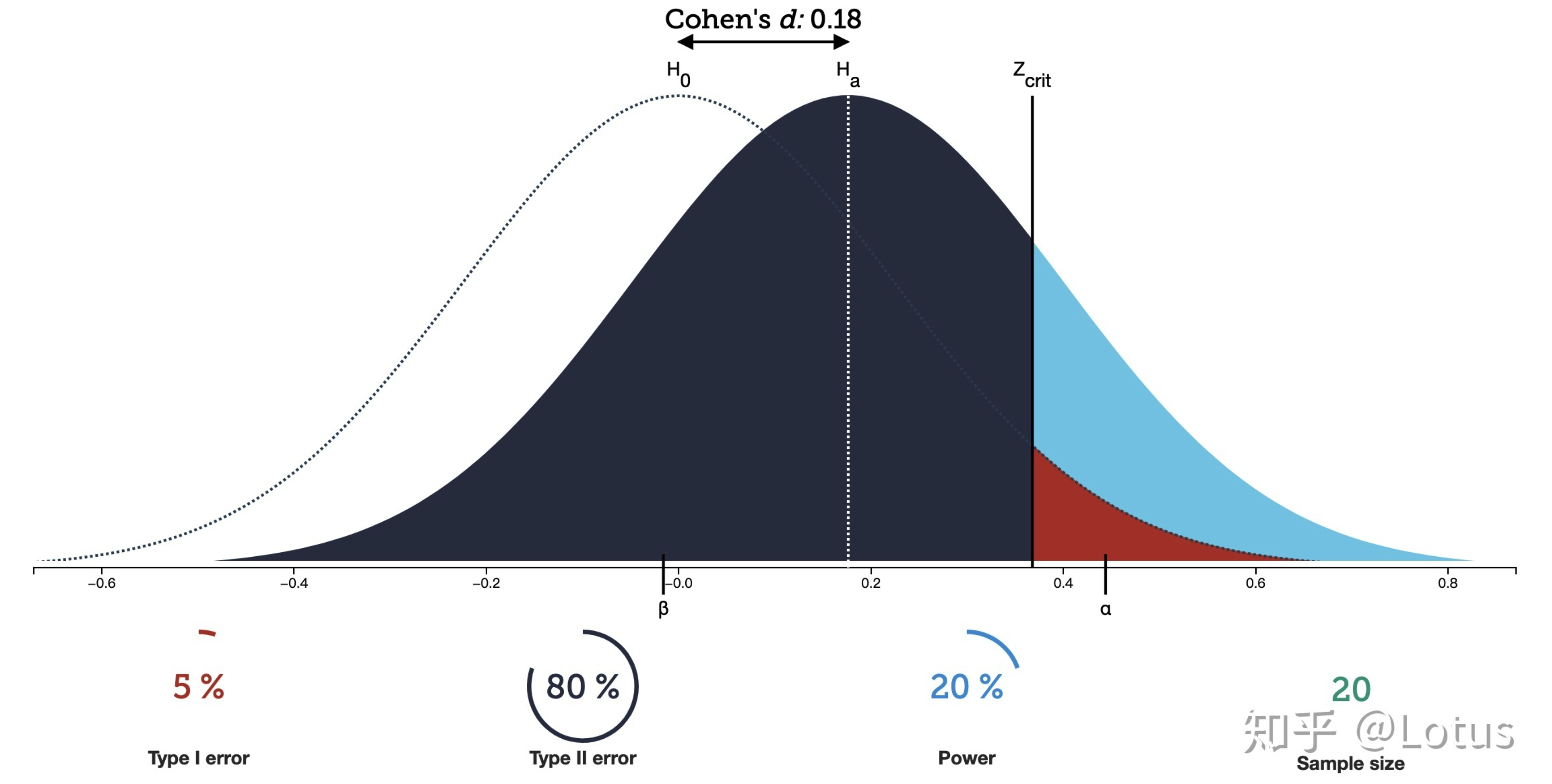
  • 如下图所示，四种因素满足知三求一
    • significance level 显著性水平
    • effective size 两组样本均值的差异(Cohen's d)
    • statistical power 统计功效
    • sample size 样本量

  • 给定α=0.05和β=0.2，对于effect size(公式中的d)就是前述的Dmin(业务上接受的指标最小变化)，接下来，计算实验需要的样本量。这个值会分为两组：对照组和实验组

  • 原假设

    • \[H_0 = P_{cont} - P_{exp} = 0 \]

  • 样本量n的计算公式如下：

    • \[n = \frac{(Z_{1-\frac{α}{2}})^2*sd_1+Z_{1-\beta}*sd_2}{d^2} \]

    • \[sd_1 = \sqrt{p(1-p)+p(1-p)} \]

    • \[sd_2 = \sqrt{p(1-p)+(p+d)(1-(1-(p+d)))} \]

# 计算sd1和sd2
def get_sds(p, d):
    sd1 = math.sqrt(2 * p * (1 - p))
    sd2 = math.sqrt(p * (1 - p) + (p + d) * (1 - (p + d)))
    x = [sd1, sd2]
    return x

# 计算z-score
def get_z_score(alpha):
    return norm.ppf(alpha)


# 计算样本量
def get_sampSize(sds, alpha, beta, d):
    n = pow((get_z_score(1 - alpha/2) * sds[0] + get_z_score(1 - beta) * sds[1]), 2) / pow(d, 2)
    return n

# 指定基线数据p和d
GC = {}
GC['p'] = baseline['GConversion']
GC['d'] = 0.01
NC = {}
NC['p'] = baseline['NConversion']
NC['d'] = 0.0075

  • 计算每个指标实验所需样本量，然后选择最大的，需要注意的是，上述计算的样本量n指的是点击了免费试用button的cookies(一次点击才代表二项分布中的一次试验)，然而，对于一次PV来说，有的用户会点击，有的不会点击，无法保证每个浏览这个页面的用户都会点击，所以需要修正样本量。

    • (1)对于课程登记转化率(Gross Conversion)：课程登记用户数(enrolled)/免费试用按钮点击量(clicks)

      • 基线数据：
页面uv=40000
button人均点击率=button点击量(clicks) / 页面uv = 3200 / 40000 = 0.08
SampSize = (SampSize / button人均点击率) * 2
这里的页面uv指的是Number of cookies who viewed the course overview page

      • GC['SampSize'] = round(get_sampSize(get_sds(GC['p'], GC['d']), 0.05, 0.2, GC['d']))
GC['SampSize'] = round(GC['SampSize'] / 0.08 * 2)
GC['SampSize']  # 645875

    • (2)全流程转化率(Net Conversion)：课程付费用户数(paid) / 免费试用按钮点击量(clicks)

      • NC['SampSize'] = round(get_sampSize(get_sds(NC['p'], NC['d']), 0.05, 0.2, NC['d']))
NC['SampSize'] = round(NC['SampSize'] / 0.08 * 2)
NC['SampSize']  # 685325

    • 可以看出685325最大，而每天日均页面uv是40000，对于这个实验，如果每天只用80%，即32000，那么大概需要21天时间积累样本。这里存在一个问题，就是21天uv必然存在重复的，这样实际收集的样本量要少于实验需要的，所以这里做了一个近似处理(UV = PV)

AB实验分析

  • 加载AB组实验数据

  • 实验健康检验

    • 对于三种理论上不会变的指标，因为策略(弹窗)实在这些行为之后才生效的，如果三种指标在A/B两组存在显著性差异，那么最终结果是不可靠的：页面UV、免费试用按钮点击量、人均点击率

    • (1)计数差异的检验

      • 分析页面UV，点击量的检验(绝对量)，分析A/B两组的差异是否显著

      • pageviews_cont = control['Pageviews'].sum()
pageviews_exp = experiment['Pageviews'].sum()
pageviews_total = pageviews_cont + pageviews_exp
print('number of pageviews in control:', pageviews_cont)  # 345543
print('number of pageviews in experiment:', pageviews_exp)  # 344660

      • 可以从结果看到，实验组和对照组的Pageviews近似一样，接下来我们需要通过假设检验的方法验证这种差异是随机性导致的，我们期待的对照组PV数值，应该是总PV的一半(50%)，如果将样本分配到对照组这个事件看作是伯努利试验中成功的事件，同时我们希望这个概率是0.5，那么分配给对照组的样本量(PV)应该满足二项分布的随机变量X

      • 当n很大时，基于中心极限定理，二项分布可以近似为正态分布

        • \[X-N(p, \sqrt{\frac{p(1-p)}{p}})，其中N是总PV \]

      • 原假设：

        • \[H_0：P=0.5 \]

      • 在5%的显著性水平下，边界误差和置信区间为

        • \[ME = Z_{1-\frac{\alpha}{2}}*SD \]

        • \[CI = [\hat p - ME, \hat p + ME] \]

        • 其中SD为标准差

    • (2)概率差异的检验

      • CTP = clicks / pv，这类指标是比例值，我们期望CTP在对照组和实验组里无显著差异，即：

        • \[CTP_{exp} - CTP_{cont} = 0 \]

      • 计算其置信区间为：

        • \[SD_{pool} = \sqrt{p_{pool}(1 - \hat p_{pool})(\frac{1}{N_{cont}} + \frac{1}{N_{exp}})} \]

        • \[其中，\hat p_{pool} = \frac{x_{cont}+x_{exp}}{N_{cont}+N_{exp}} \]

p = 0.5
alpha = 0.05
p_hat = round(pageviews_cont / pageviews_total, 4)
sd = math.sqrt(p * (1 - p) / pageviews_total)
ME = round(get_z_score(1 - (alpha / 2)) * sd, 4)
print('置信区间的范围在', p-ME, '和', p+ME, '之间，样本值是', p_hat)
# 置信区间的范围在 0.4988 和 0.5012 之间，样本值是 0.5006
# 可以看出,对照组样本比例是0.5006在置信区间范围内，所以pv(页面uv)这个指标是通过检验的,不存在显著差异。

# 同理,对于点击量clicks
clicks_cont = control['Clicks'].sum()
clicks_exp = experiment['Clicks'].sum()
clicks_total = clicks_cont + clicks_exp
p_hat = round(clicks_cont / clicks_total, 4)
sd = math.sqrt(p * (1 - p) / clicks_total)
ME = round(get_z_score(1 - (alpha / 2)) * sd, 4)
print('置信区间的范围在', p-ME, '和', p+ME, '之间，样本值是', p_hat)
# 置信区间的范围在 0.4959 和 0.5041 之间，样本值是 0.5005

ctp_cont = clicks_cont / pageviews_cont
ctp_exp = clicks_exp / pageviews_cont
d_hat = round(ctp_exp - ctp_cont, 4)
p_pooled = clicks_total / pageviews_total
sd_pooled = math.sqrt(p_pooled * (1 - p_pooled) * (1 / pageviews_cont + 1 / pageviews_exp))
ME = round(get_z_score(1 - (alpha / 2)) * sd_pooled, 4)
print(f'置信区间的范围在，{0-ME}和{0+ME}之间，样本值是{d_hat}')
# 置信区间的范围在，-0.0013和0.0013之间，样本值是-0.0002
# CTP指标也通过检验了,到此为止，第一类指标全部通过检验。

  • 用两总体比例之差检验，原理(贾俊平统计学)如下：

    • 设两个总体服从二项分布，这两个总体中具有某种特征单位数的比例分别为π1和π2，但π1和π2未知，可以用样本比例p1和p2代替，检验两个总体比例相等的假设：

      • \[H_0:π_1 - π_2 = 0 或 H_0:π_1 = π_2 \]

    • 在原假设成立的条件下，最佳的方差是p(1-p)，其中p是将两个样本合并后得到的比例估计量，即：

      • \[p = \frac{x_1 + x_2}{n_1 + n_2} = \frac{p_1n_1+p_2n_2}{n_1 + n_2} \]

    • 式中，x1表示样本n1中具有某种特征的单位数；x2表示样本n2中具有某种特征的单位数。

    • 在大样本条件下，统计量z的表达式为：

      • \[z = \frac{p_1 - p_2}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}} \]

  • 核心-策略相关指标检验

    • 策略相关指标检验是A/B实验的价值所在，检验策略相关指标差异的显著性，即判断策略给公司带来的收益是显著的还是不显著的，不显著可能就不值得上线，这种显著是正收益还是负收益。注意：给定数据中enrollments和payments两列有缺失值，所有在检验这部分相关指标时，真正有效的数据只有23天的，包括：
      • 课程登记转化率(Gross Conversion)：课程登记用户数(enrolled) / 免费试用按钮点击量(clicks)
      • 全流程转化率(Net Conversion)：课程付费用户数(paid) / 免费试用按钮点击量(clicks)
# 统计实验组和对照组各自有效的点击量
clicks_cont = control['Clicks'].loc[control['Enrollments'].notnull()].sum()
clicks_exp = experiment['Clicks'].loc[experiment['Enrollments'].notnull()].sum()
display(clicks_cont, clicks_exp)  # 17293,17260

# 检验课程登记转化率(Gross Conversion)如下，这里检验仍是两总体比例之差检验：
enrollments_cont = control['Enrollments'].sum()
enrollments_exp = experiment['Enrollments'].sum()
GC['d_min'] = 0.01
GC_cont = enrollments_cont / clicks_cont
GC_exp = enrollments_exp / clicks_exp
GC_pooled = (enrollments_cont + enrollments_exp) / (clicks_cont + clicks_exp)
GC_sd_pooled = math.sqrt(GC_pooled * (1 - GC_pooled) * (1 / clicks_cont + 1 / clicks_exp))
GC_ME = round(get_z_score(1 - alpha / 2) * GC_sd_pooled, 4)
GC_diff = round(GC_exp - GC_cont, 4)
print(f'因为策略造成的指标变化：{GC_diff*100}%')
print(f'置信区间：[{GC_diff-GC_ME},{GC_diff+GC_ME}]')
# 因为策略造成的指标变化：-2.06%
# 置信区间：[-0.0292,-0.012]
# 可以看出差异的置信区间不包括0，所有策略造成的指标变化在统计上是显著的
# 但是是否在现实意义上是显著的，需要与D_min比较，GC的D_min是0.01，实验差异大于0.01，所以这个差异在现实意义上也是显著的
# 课程登记转化率指标是显著减少的(-2.06%)，在点击量差异不显著的情况下，说明实验策略有效的减少了课程登记用户数，弹窗有效的阻挡了一部分用户登记课程

# 全流程转化率(Net Conversion)如下:
payments_cont = control['Payments'].sum()
payments_exp = experiment['Payments'].sum()
NC_cont = payments_cont / clicks_cont
NC_exp = payments_exp / clicks_exp
NC_pooled = (payments_cont + payments_exp) / (clicks_cont + clicks_exp)
NC_sd_pooled = math.sqrt(NC_pooled * (1 - NC_pooled) * (1 / clicks_cont + 1 / clicks_exp))
NC_ME = round(get_z_score(1 - alpha / 2) * NC_sd_pooled, 4)
NC_diff = round(NC_exp - NC_cont, 4)
print(f'因为策略造成的指标变化：{NC_diff*100}%')
print(f'置信区间：[{NC_diff-NC_ME},{NC_diff+NC_ME}]')
# 因为策略造成的指标变化：-0.49%
# 置信区间：[-0.0116,0.0018]
# 误差的置信区间不包括-0.49%，NC的D_min是0.75%，所以指标差异在统计上是显著的，但在现实意义上不显著，即收益不显著

双重检验-符号检验

我们可以通过符号检验(Sign Test)获得对实验结果的另外一个视角分析，检验观察结果每天的变化趋势是否显著。可以通过每天的指标值，统计对照组指标数值低于实验组的次数，将对照组指标数值较低这个时间，作为伯努利试验中成功的事件。

  • 数据准备

    • # 连接器实验组与对照组，同时实验组指标名都加上_exp后缀，对照组一样
full = control.join(other=experiment, how='inner', lsuffix='_cont', rsuffix='_exp')
# 不要有缺失值的数据
full = full.loc[full['Enrollments_cont'].notnull()]
full.count()
'''
Date_cont           23
Pageviews_cont      23
Clicks_cont         23
Enrollments_cont    23
Payments_cont       23
Date_exp            23
Pageviews_exp       23
Clicks_exp          23
Enrollments_exp     23
Payments_exp        23
dtype: int64
'''

# 对于GC和NC指标，比较每天实验组与对照组指标数值的大小
x = full['Enrollments_cont'] / full['Clicks_cont']
y = full['Enrollments_exp'] / full['Clicks_exp']
full['GC'] = np.where(x<y, 1, 0)

z = full['Payments_cont'] / full['Clicks_cont']
w = full['Payments_exp'] / full['Clicks_exp']
full['NC'] = np.where(z<w, 1, 0)
print(full[['Date_cont', 'GC', 'NC']])
'''
      Date_cont  GC  NC
0   Sat, Oct 11   0   0
1   Sun, Oct 12   0   1
2   Mon, Oct 13   0   0
3   Tue, Oct 14   0   0
4   Wed, Oct 15   0   1
5   Thu, Oct 16   0   0
6   Fri, Oct 17   0   0
7   Sat, Oct 18   0   0
8   Sun, Oct 19   0   1
9   Mon, Oct 20   0   1
10  Tue, Oct 21   0   0
11  Wed, Oct 22   0   0
12  Thu, Oct 23   0   1
13  Fri, Oct 24   0   0
14  Sat, Oct 25   0   0
15  Sun, Oct 26   0   0
16  Mon, Oct 27   0   0
17  Tue, Oct 28   1   1
18  Wed, Oct 29   1   1
19  Thu, Oct 30   1   0
20  Fri, Oct 31   1   1
21   Sat, Nov 1   0   1
22   Sun, Nov 2   0   1
'''

# 计算实验组比对照组指标值更高的天数
GC_x = full.GC[full['GC'] == 1].count()
NC_x = full.NC[full['NC'] == 1].count()
n = full.NC.count()
print(f'GC:{GC_x}\nNC:{NC_x}\ntotal_days:{n}')
# GC:4
# NC:10
# total_days:23

  • 符号检验

    • 当我们计算出实验组比对照组指标值更高的天数后，接下来，就是检验这个值是否显著，假设每天产生这种结果是随机的(50%)，因此，根据p=0.5和n=天数的二项分布，S+表示这个事件(实验组的指标值更高)成功发生的天数，这也是检验统计量。

    \[p(success) = \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} \]

    • 若S+<n/2，则计算p(x<=S+)，若S+>n/2，则计算p(x>=S+)，用p值作为检验，p值的定义为：当原假设为真的时候，比所得到的样本观察结果更极端的结果出现的概率，例如观察结果是2，则：

      • \[p-value =p(x<=2)=p(0) + p(1) + p(2) \]

    • def get_prob(x, n):
    p = round(math.factorial(n) / (math.factorial(x) * math.factorial(n - x)) * 0.5**x*0.5**(n-x), 4)
    return p
  
def get_2side_pvalue(x, n):
    p = 0
    for i in range(0, x+1):
        p += get_prob(i, n)
    return 2*p

# 与显著性水平0.05进行比较
print(f'GC Change is significant if {get_2side_pvalue(GC_x, n)} is samller than 0.05')
print(f'NC Change is significant if {get_2side_pvalue(NC_x, n)} is samller than 0.05')
# GC Change is significant if 0.0026 is samller than 0.05
# NC Change is significant if 0.6774 is samller than 0.05
# GC指标变化显著，NC指标变化不显著，结合上文参数检验结果，可以确认结论

结论

  • 对于三个预期不会变的指标，全部通过检验，说明除了策略影响外，A/B两组没有受到外界不可知因素影响，这是后面结论可靠的前提。实际AB实验中，可能会出现抽样不均的情况，为了保证实验数据的变化仅仅是实验本身引起的，可以一次性抽取4，5组流量，不加策略空跑，监控核心指标数据，选取两组数据最接近的上实验(控制变量)，即AA实验，相比AB实验，AA实验是预先控制好变量，减少不确定因素带来的误差。
  • 对于第二类评估指标的检验结果：课程登记转化率(Gross Conversion)变化显著，即实验组课程登记数减少显著；全流程转化率(Net Conversion)变化不显著(参数检验统计显著，现实业务不显著，符号检验不显著)，说明策略没有影响到付费用户

其它

  • 关于对照组和实验组样本独不独立的问题，如果将实验组和对照组近似为独立的，将每一天的数据看做配对，然后检验差值是否显著，用配对样本t检验；如果认为实验组和对照组不是独立的，汇总全部的数据，求总的比例，用z检验

  • 如何计算业务上允许的最小变化D_min

    • D_min：业务上允许的最小变化，即A/B实验除p值、置信区间外另外一个阈值，也被称为effect size，两组样本均值的差异(Cohen's d)

    • D_min计算方法如下(正态分布算法)：

      • 假设有k天数据，则没分流量在对应指标上取k天的均值

      • 将n份流量对应指标两两相减，共得n0=Cn2个差值，将差值样本记为D

      • 差值总体分布 vs 0，做z检验

      • 在α=0.05下，求得拒绝阈值

        • \[C: \bar {|D|} >= φ_{0.975}\frac{S_D}{\sqrt{n_0}}=C \]

  • t-检验

    • 确定实验周期，一般为7天

    • 确定实验所需样本量

      • 如何决定样本的数量？太多了会浪费很多资源，太少了会因为统计灵敏度太低而得不到显著的结论，可以利用功效分析：第一类错误α不超过5%，即Significance Level(显著性水平)=5%；第二类错误β不超过20%，即Statistical Power(统计功效)=1-β=80%
      • 直观上理解，AB两组即使有差异，也不一定被你观测出来，必须保证一定的条件(比如样本要充足)才能使你观测出统计量之间的差异；而统计功效就是当AB两组实际有差异时，能被我们检测出出差异的概率(当备择假设为真，我们接受的概率)，利用功效函数反推样本量，计算公式见前述示例。

    • 配对样本t-检验

      • 设实验组、对照组有n天数据，则：

      \[X = {X_1, X_2, ..., X_n} \]

      \[Y = {Y_1, Y_2, ..., Y_n} \]

      • 做配对t-检验，令：

      \[Z = {Z_1, Z_2, ..., Z_n}，其中Z_i= X_i- Y_i, i=1, 2, ..., n \]

      • 有统计量

      \[T= \frac{\sqrt{n}*\sqrt{Z}}{S_Z} 服从 t(n-1) \]

      • 拒绝域

      \[W=P(|T| >= t_{1-\frac{\alpha}{2}}(n-1)) \]

      • p值

      \[p=2*t_{n-1}(|T|) \]

      • 在部分情况下，要更小的p值才能拒绝原假设，会使第一类错误概率降低，第二类错误概率提高，要使第二类错误概率不过高，可以通过增加样本量来解决
      • 决策方案：
        • 正收益：确定发布新版本
          • 进一步验证实验是否正确-实验反转，对照组变成实验组，实验组变成对照组。但需要注意的是，建议只在实验为正向收益时反转实验，如果收益为负，反转实验，只会多损伤原对照组用户的体验
        • 负收益：优化迭代方案重新开发
        • 持平：调整分流比例，继续测试

AB Test在业务运用上的常见场景

  • 如何选择正确的实验指标，一般A/B实验指标体系需要三类实验指标

    • 核心指标：这种指标是决定实验成败的关键指标
      • 需要依据具体的业务理解，明白实验的目标，进而做出选择，避免选择虚荣指标作为核心指标
    • 辅助指标：用于辅助判断实验对其它因素的影响
      • 漏斗细分部分转化率、重要下游指标、其它关键用户指标
    • 反向指标：实验可能产生负面影响的指标
      • 反向指标的作用是提示实验可能的负面影响，如果负面影响太高，即使其它指标通过，也可以否决实验结果

  • AB测试中的常见问题

    • 新奇效应-实验时间对统计显著性的影响
      • 新奇效应，也称均值回归，在统计学上指的是对于概率事件的结果，随着试验次数的增加，结果往往趋近于均值。举个例子，假设让一个人回答若干个历史问题，这些问题是从庞大的题目数据库里随机抽取的，那么这个人一次测试的分数很有可能高于他自身能力获得的分数(超长发挥)，也可能低于，但是若干次测试后，分数会接近他的真是平均水平
      • AB测试中，试验早起用户因为新奇会关注新改动，但是往往前期显著的提升在之后几天或者几周的测试中会逐渐消失
    • 以偏概全-实验周期是否覆盖产品高低频用户
      • 如果实验时间跑的太短，没有让高频用户和低频用户都包含在实验里，那么实验结果就是有偏的。
    • 辛普森悖论-实验流量分割比例改变带来的结果错误
      • 辛普森悖论是英国统计学家E.H.辛普森于1951年剔除的悖论，即在某个条件下的两组数据，分别讨论时都会满足某种性质，但是一单合并考虑，却可能导致相反的结论。如：男生点击率增加，女生点击率增加，为何总体点击率减少？因为男女的点击率可能有较大差异，且低点击率群体的占比增大。如原来男性20人，点击1人；女性10偶人，点击99人，总点击率100/120。现在男性100人，点击6人；女性20人，点击20人，总点击率26/120。
      • 如何才能在AB测试的设计、实施以及分析的时候，规避辛普森悖论造成的各种大坑呢？最重要的一点是，要得到科学可信的AB测试试验结果，就必须合理的进行正确的流量分割，保证试验组合对照组里的用户特征是一致的，并且都具有代表性，可以代表总体用户特征。

  • 正交实验-如何同时进行多个实验，保证流量的高可用

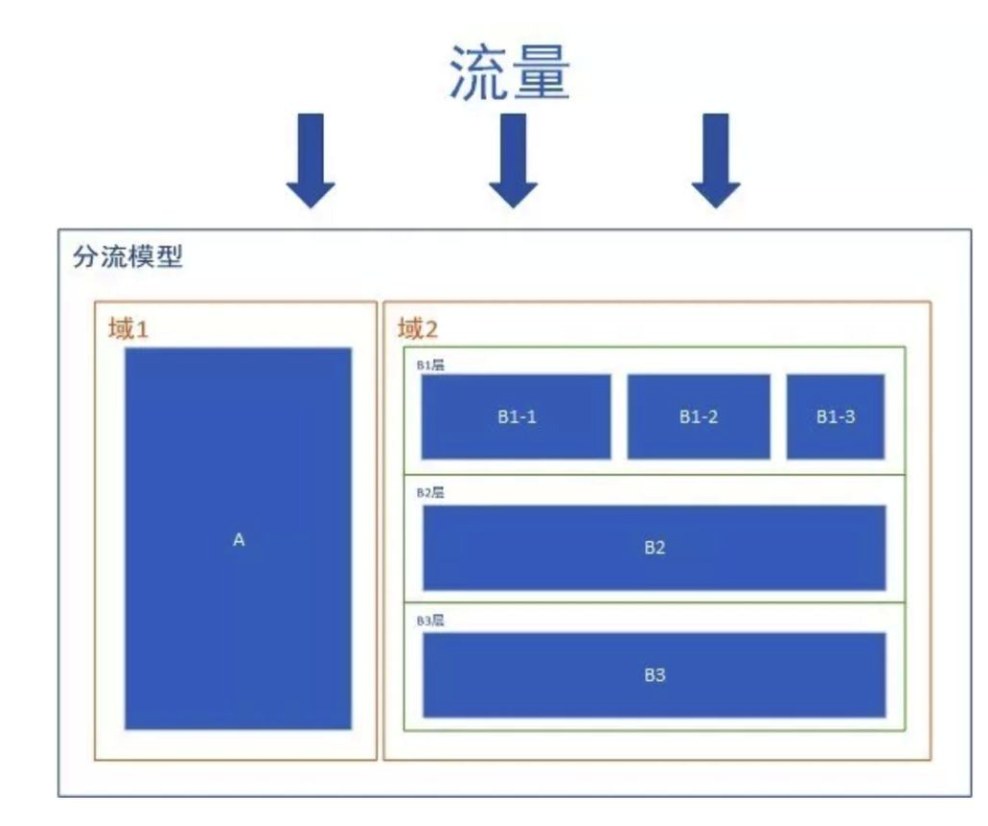
    • 在实验版本的设计过程中，还需要考虑线上进行多个实验相互之间的影响，AB实验的抽样流量架构需要利用流量分层分流机制来保证流量的高可用，流量分层分流机制主要涉及两个概念：正交和互斥。层与层之前的流量被称为正交关系，互斥与正交的概念分别对应流量分层分流机制中的域和层的概念。

  • 域1和域2拆分流量，此时域1和域2是互斥的；流量流过域2中的B1层、B2层、B3层时，B1层、B2层、B3层的流量都是与域2的流量相等(流量的复用)，此时B1层、B2层、B3层的流量是正交的；流量流过域2中的B1层时，又把B1层分为了B1-1，B1-2，B1-3，此时B1-1，B1-2，B1-3之间又是互斥的。根据以上规则，我们可以不断的在此模型中增加域、层，并且可以相互嵌套，这要与时间的业务相匹配，拆分过多的结构可能会把简单的业务复杂化，拆分过少的结构又可能不满足实际业务。

  • 例：B1层、B2层、B3层可能分别为：UI层、搜索结果层、广告结果层，这几层基本上是没有任何的业务关联度的，即使共用相同的流量(流量正交)也不会对实际的业务造成影响。但是如果不同层之间所进行的试验相互关联，如B1层是修改的一个页面的按钮文字颜色，B2层是修改的按钮的颜色，当按钮文字颜色和按钮颜色一样时，该按钮已经是不可用的了。因此同一类的实验在同一层内进行，并且需要考虑到不同实验互相的依赖。

  • 总结

    • 流量正交让业务关联度很小的实验有足够的流量同时进行(实现流量的高可用)
    • 流量互斥让业务关联度较大的实验流量分开，避免该绕，保证实验结果的可信度

  • 如何分析实验结果背后的原因：如果预期改动的可以提升的某个指标，反而下降了，该如何分析

    • 细分漏斗：看具体是漏斗转化路径上的哪一步与假设不符
    • 分维度拆分
      • 用户分群：对实验结果进行分群分析，看总体实验结果在用户分解之后是否一致，是否某一个版本在某一类用户表现好，而在另外一类用户表现差？
      • 分位置拆分：对于点击率实验，可以把页面总体点击率拆分为分位置点击率，然后针对页面内容与用户需求，做一一对应分析
    • 用户调研
    • 后续实验：针对结果形成新的假设，进行后续实验，验证假设
posted @ 2021-11-08 16:40  lotuslaw  阅读(576)  评论(0)  编辑  收藏  举报