第一章 绪论

第一章 绪论

机器学习概述

机器学习是这样一门学科，它致力于研究如何通过计算的手段，利用经验来改善系统自身的性能。在计算机系统中，“经验”通常以“数据”形式存在，因此机器学习所研究的主要内容，是关于在计算机上从数据中产生“模型”的算法，即“学习算法”。

有了学习算法，我们把经验数据提供给它，他就能基于这些数据产生模型；在面对新的情况时，模型会给我们提供相应的判断。如果说计算机科学是研究关于“算法”的学问，那么类似的，可以说机器学习是研究关于“学习算法”的学问。

基本术语

• 数据集

• 事件/对象

• 示例/样本

• 属性/特征

• 属性值

• 属性空间/样本空间/输入空间

• 特征向量

  由于空间中的每个点对应一个坐标向量，因此我们也把一个示例称为一个“特征向量”

• \[D={x1,x2,...,xm}表示包含m个示例的数据集 \]

• 每个实例由d个属性描述，则每个示例：

  \[x_i=(x_{i1};x_{i2};...;x_{id}) 是d维样本空间X的一个向量，x_i\in X \]
  \[其中x_{ij}是x_i在第j个属性上的取值，d成为样本x_i的维数。 \]

• 学习/训练

  从数据中学得模型得过程称为“学习”或“训练”。

• 训练数据

• 训练样本

• 训练集

  训练样本组成的集合称为训练集。

• 假设

  学得模型对应了关于数据的某种潜在的规律，因此亦称“假设”；这种潜在规律自身则称为“真相”/“真实”。

• 模型/学习器

• 标记

  关于示例结果的信息，称为“标记”。

• 样例

  拥有了标记信息的示例，则称为样例。

  \[一般地，用(x_i,y_i)表示第i个样例，其中y_i\in Y是示例x_i得标记 \]
  \[Y是所有标记的集合，亦称“标记空间”或“输出空间”。 \]

• 分类

  若我们预测的是离散值，此类学习任务称为“分类”。

• 回归

  若我们预测的是连续值，此类学习任务称为"回归"。

• 二分类

  只涉及两个类别的分类任务。正例/反例

• 预测任务

  \[预测任务是希望通过对训练集{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}进行学习， \]
  \[建立一个从输入空间X到输出空间Y的映射f：X\longrightarrow Y \]
  \[(1)对于二分类任务，通常令Y={-1，+1}或{0，1} \]
  \[(2)对于多分类任务，|Y|>2;对于回归任务，Y\in R，R为实数集 \]

• 测试

  使用模型进行预测的过程

• 测试样本

• 聚类

  将训练集中的样本分成若干组，每个组称为一个簇，这些自动形成的簇可能对应一些潜在的概念划分。

• 监督学习

  训练数据集拥有标记信息的学习任务。

  分类和回归。

• 无监督学习

  训练数据集不包含标记信息的学习任务。

  聚类。

• 泛化

  学得模型适用于新样本的能力称为“泛化”能力。

• 独立同分布假设

  通常假设样本空间中全体样本服从一个未知分布D，我们获得的每个样本都是独立同分布地从这个分布上采样获得的，即“独立同分布”。

假设空间

• 归纳与演绎

  归纳与演绎是科学推理的两大基本手段，前者是从特殊到一般的“泛化”过程，后者则是从一般到特殊的“特化”过程。

  从“样例中学习”显然是一个归纳的过程，因此亦称“归纳学习”。

• 归纳学习

  归纳学习分为侠义归纳学习和广义归纳学习。

  广义的归纳学习大体相当于从样例中学习，而狭义的归纳学习则要求从训练数据中学得概念，因此亦称概念学习或概念形成。

• 概念学习

  概念学习中最基本的是布尔概念学习，即对“是”“不是”这样的可表示为0/1布尔值的目标概念的学习。

• 学习过程

  我们可以把学习过程看作一个在所有假设组成的空间中进行搜索的过程，搜索目标是找到与训练集“匹配”的假设，即能够将训练集中的瓜判断正确的假设。

• 版本空间

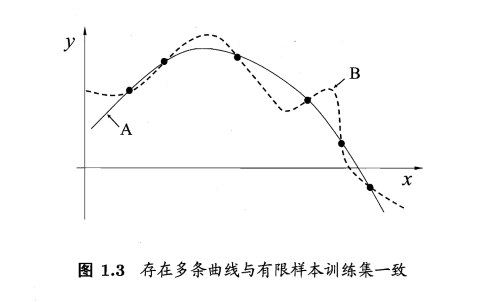
  需注意的是，现实问题中我们常面临很大的假设空间，但学习过程是基于有限样本训练集进行的，因此，可能有多个假设与训练集一致，即存在着一个与训练集一致的“假设集合”，我们称之为“版本空间”。

归纳偏好

• 归纳偏好

  机器学习算法在学习过程中对某种类型假设的偏好，称为“归纳偏好” , 或简称为“偏好”。

  任何一个有效的机器学习算法必有其归纳偏好，否则它将被假设空间中看似在训练集上“等效”的假设所迷惑，而无法产生确定的学习结果。

若认为相似的样本应有相似的输出(例如，在各种属性上都比较像的西瓜，成熟程度应该比较接近)，则对应的学习算法可能偏好图中比较“平滑”的曲线A而不是比较“崎岖”的曲线B，反之则相反。

• 奥卡姆剃刀

  一般性的原则来引导算法确立“正确的”偏好。

  “奥卡姆剃刀”是一种常用的、自然科学研究中最基本的原则，即“若有多个假设与观察一致，则选择最简单的那个”。

• NFL(No Free Lunch Throrem)定理

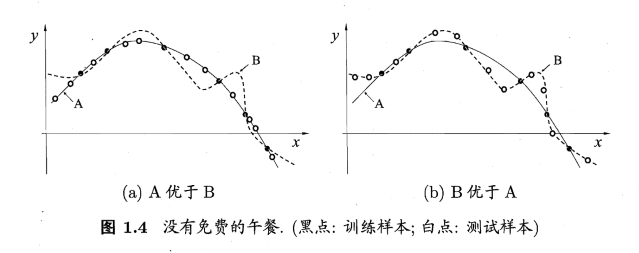
  “没有免费的午餐”定理。

对于一个学习算法A，若它在某 些问题上比学习算法B好，则必然存在另一些问题，在那里B比A好。有趣的是，这个结论对任何算法均成立。

NFL定理有一个重要前提：所有“问题”出现的机会相同、或所有问题同等重要。但实际情况并不是这样，很多时候，我们只关注自己正在试图解决的问题(例如某个具体应用任务)，希望为它找到一个解决方案，至于这个解决方案在别的问题、甚至在相似的问题上是否为好方案，我们并不关心。

所以NFL定理最重要的寓意，是然我们清楚地认识到，脱离具体问题，空泛地谈论“什么学习算法更好”毫无意义，因为若考虑所有潜在地问题，则所有学习算法都一样好。

学习算法自身的归纳偏好于问题是否相配，往往会起到决定性的作用。

发展历程

• 二十世纪五十年代到七十年代初，人工只能研究处于“推理期”，那时人们以为只要赋予机器逻辑推理能力，机器就能具有智能。

  逻辑理论家程序

  通用问题求解程序

• 五十年代中后期，基于神经网络的“连接主义”学习开始出现。

  感知机

• 在六七十年代，基于逻辑表示的“符号主义”学习技术蓬勃发展。

  结构学习系统

  基于逻辑的归纳学习系统

  概念学习系统

• 二十世纪八十年代是机器学习称为一个独立的科学领域、各种机器学习技术百花初绽的时期。

• 从“样例中学习”(也就是广义的归纳学习)，它涵盖了监督学习、无监督学习等。

• 在二十世纪八十年代，“从样例中学习”的一大主流是符号主义学习，其代表包括决策树和基于逻辑的学习。

  典型的决策树学习以信息论为基础，以信息熵(在信息论中，熵被用来衡量一个随机变量出现的期望值，它代表了在被接收之前，信号传输过程中损失的信息量又被称为信息熵)的最小化为目标。

  基于逻辑的学习的著名代表是归纳逻辑程序设计，可看作机器学习于逻辑程序设计的交叉。

• 二十世纪九十年代中期之前，“从样例中学习”的另一主流技术是基于神经网络的连接主义学习。

  与符号主义学习能产生明确的概念表示不同，连接主义学习产生的是“黑箱”模型，因此从知识获取的角度来看，连接主义学习技术有明显弱点。

• 二十世纪九十年代中期，“统计学习”闪亮登场并迅速占据主流舞台。

  支持向量机

  核方法

• 二十一世纪初，连接主义学习又卷土重来，掀起了以“深度学习”为名的热潮，所谓深度学习，狭义地说就是“很多层”的神经网络。

  深度学习技术涉及的模型复杂度非常高，以至于只要下功夫“调参”，把参数调节好，性能往往就好，因此，深度学习虽然缺乏严格的理论基础，但它显著降低了机器学习应用者的门槛。

应用现状

谈到对数据进行分析利用，很多人会想到“数据挖掘”，数据挖掘领域在二十世纪九十年代形成，它受到很多科学领域的影响，其中数据库、机器学习、统计学习无疑影响最大。

数据挖掘是从海量数据中挖掘知识，这就必然涉及对“海量数据”的管理和分析。大体来说，数据库领域的研究为数据挖掘提供数据管理技术，而机器学习和统计学的研究为数据挖掘提供数据分析技术。