【算法设计】
二 分治策略
2.1 最大子数组问题
分治算法
分治法是一种将问题分解成子问题递归解决的算法思想,用于求解连续最大子数组问题非常合适。该问题的目标是找到数组中连续子数组的最大和。
算法解释
-
分解:将数组划分为左右两个子数组,分别求解左右子数组的最大子数组和。
-
合并:最大子数组可能出现在:
- 左子数组中
- 右子数组中
- 跨越中间的数组中
-
递归求解:递归地分解子数组,直到子数组大小为1,此时直接返回数组的唯一元素作为最大子数组和。
-
跨越中间的情况:在数组中心位置左右两边分别向外扩展,找到左边最大和的子数组以及右边最大和的子数组,它们的和即为跨越中心的最大子数组和。
-
合并结果:最终最大子数组和为上面三种情况中的最大值。
算法复杂度
- 时间复杂度:(O(n \log n)),其中 (n) 是数组的长度。每次分解子数组需要 (O(\log n)) 次,每次合并子问题需要 (O(n)) 时间。
- 空间复杂度:由于递归调用栈空间的消耗,复杂度为 (O(\log n))。
C++代码实现
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 辅助函数:计算跨越中间的最大子数组和
int maxCrossingSum(const vector<int>& arr, int left, int mid, int right) {
int leftSum = INT_MIN, rightSum = INT_MIN;
int sum = 0;
// 从中间向左扫描,找到左半部分的最大子数组和
for (int i = mid; i >= left; i--) {
sum += arr[i];
leftSum = max(leftSum, sum);
}
sum = 0;
// 从中间向右扫描,找到右半部分的最大子数组和
for (int i = mid + 1; i <= right; i++) {
sum += arr[i];
rightSum = max(rightSum, sum);
}
// 返回跨越中间的最大和
return leftSum + rightSum;
}
// 主函数:分治法求解最大子数组和
int maxSubArraySum(const vector<int>& arr, int left, int right) {
// 基本情况:只有一个元素
if (left == right) {
return arr[left];
}
// 取中间点
int mid = (left + right) / 2;
// 递归计算左半部分、右半部分和跨中间的最大子数组和
int leftMax = maxSubArraySum(arr, left, mid);
int rightMax = maxSubArraySum(arr, mid + 1, right);
int crossMax = maxCrossingSum(arr, left, mid, right);
// 返回三者中的最大值
return max({leftMax, rightMax, crossMax});
}
int main() {
vector<int> arr = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
int n = arr.size();
int maxSum = maxSubArraySum(arr, 0, n - 1);
cout << "最大子数组和为: " << maxSum << endl;
return 0;
}
代码说明
maxCrossingSum函数:计算从mid向左、向右扩展得到的跨越中间的最大子数组和。maxSubArraySum函数:实现分治算法,递归求解左右和跨越中间的最大子数组和,并返回三者的最大值。main函数:创建一个测试数组并调用maxSubArraySum求解。
Kadane算法
求解连续最大子数组问题(即最大子数组和问题)最常见的算法是Kadane’s Algorithm。该算法的时间复杂度为 (O(n)),可以高效地找到最大子数组的和。
算法解释
假设给定一个包含 ( n ) 个整数的数组 arr,我们需要找到和最大的连续子数组。Kadane算法的核心思想是通过动态规划来解决这个问题,即通过局部最优解推导出全局最优解。
-
定义两个变量:
current_max:记录包含当前元素的最大子数组和。global_max:记录全局的最大子数组和。
-
初始化:
current_max和global_max初始化为数组的第一个元素的值arr[0]。
-
迭代数组:
- 从第二个元素开始遍历数组,对每个元素
arr[i]执行以下步骤:- 更新
current_max为max(arr[i], current_max + arr[i]),即判断当前元素单独作为新子数组的开始,还是继续累加前面的和更大。 - 更新
global_max为max(global_max, current_max),即检查当前的current_max是否大于记录的global_max,如果是则更新。
- 更新
- 从第二个元素开始遍历数组,对每个元素
-
结果:
- 遍历完成后,
global_max即为最大子数组的和。
- 遍历完成后,
代码实现
#include <iostream>
#include <vector>
#include <algorithm>
int maxSubArray(const std::vector<int>& arr) {
// 初始值设为数组第一个元素
int current_max = arr[0];
int global_max = arr[0];
// 从第二个元素开始遍历
for (size_t i = 1; i < arr.size(); i++) {
// 更新 current_max,决定是否开始新的子数组
current_max = std::max(arr[i], current_max + arr[i]);
// 更新 global_max,如果 current_max 更大则更新
global_max = std::max(global_max, current_max);
}
return global_max;
}
int main() {
std::vector<int> arr = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
int result = maxSubArray(arr);
std::cout << "最大子数组和为: " << result << std::endl;
return 0;
}
示例运行
对于输入数组 { -2, 1, -3, 4, -1, 2, 1, -5, 4 }:
- 该算法找到的最大子数组是
{4, -1, 2, 1},其和为6。
复杂度分析
- 时间复杂度:(O(n)),因为只需遍历数组一次。
- 空间复杂度:(O(1)),仅使用了几个额外变量。
2.2 Strassen矩阵乘法
高效解决矩阵乘法有几种常用的算法,经典的算法是Strassen算法。它使用分治法,将两个矩阵递归分块,从而减少矩阵乘法的乘积计算量。相比于传统的矩阵乘法算法,Strassen算法的时间复杂度更低。
传统矩阵乘法的时间复杂度
对于两个 n阶方阵 A和B,传统的矩阵乘法算法时间复杂度为 O(n^3),因为每个元素都需要计算 n 次乘法和加法。
Strassen算法简介
Strassen算法的关键思想是将矩阵分块并递归处理,使得矩阵乘法的时间复杂度降为 ( O(n^{\log_2 7}) \approx O(n^{2.81}) )。
算法步骤
-
分解:将两个矩阵 A和B 各自划分成 ( 2 \times 2 ) 的四个子矩阵:
- 对于矩阵 ( A ),将其分成四个子矩阵 ( A_{11}, A_{12}, A_{21}, A_{22} )。
- 对于矩阵 ( B ),将其分成四个子矩阵 ( B_{11}, B_{12}, B_{21}, B_{22} )。
-
递归计算:Strassen算法定义了七个辅助矩阵,通过这些辅助矩阵的加减运算,能够更高效地求出结果:
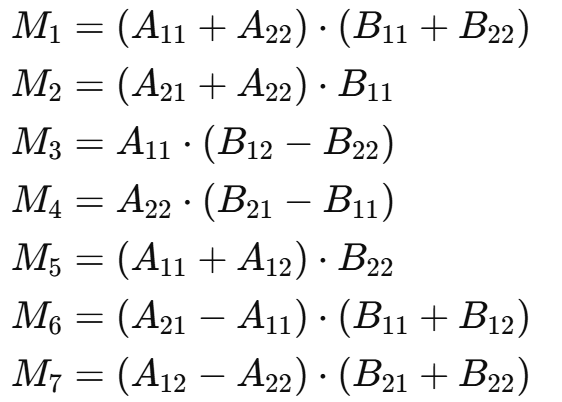
-
合并结果:根据上面计算的七个矩阵,得到结果矩阵 ( C ) 的四个子矩阵:
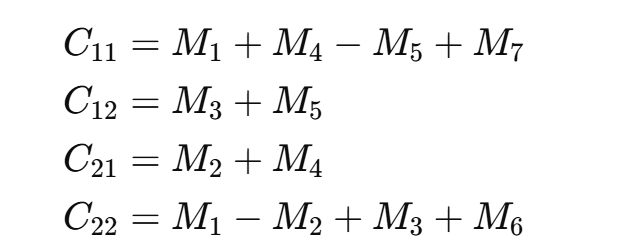
-
递归终止:当矩阵大小达到 1 时,直接进行数值乘法。
C++代码实现
以下代码实现了Strassen算法的矩阵乘法,假设矩阵大小为 ( 2^k \times 2^k )(即大小是2的幂次方)。
#include <iostream>
#include <vector>
using namespace std;
typedef vector<vector<int>> Matrix;
// 矩阵相加
Matrix add(const Matrix& A, const Matrix& B) {
int n = A.size();
Matrix result(n, vector<int>(n, 0));
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
result[i][j] = A[i][j] + B[i][j];
return result;
}
// 矩阵相减
Matrix subtract(const Matrix& A, const Matrix& B) {
int n = A.size();
Matrix result(n, vector<int>(n, 0));
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
result[i][j] = A[i][j] - B[i][j];
return result;
}
// Strassen算法核心函数
Matrix strassen(const Matrix& A, const Matrix& B) {
int n = A.size();
if (n == 1) {
return Matrix{{A[0][0] * B[0][0]}};
}
int newSize = n / 2;
Matrix A11(newSize, vector<int>(newSize)), A12(newSize, vector<int>(newSize)),
A21(newSize, vector<int>(newSize)), A22(newSize, vector<int>(newSize)),
B11(newSize, vector<int>(newSize)), B12(newSize, vector<int>(newSize)),
B21(newSize, vector<int>(newSize)), B22(newSize, vector<int>(newSize));
for (int i = 0; i < newSize; ++i) {
for (int j = 0; j < newSize; ++j) {
A11[i][j] = A[i][j];
A12[i][j] = A[i][j + newSize];
A21[i][j] = A[i + newSize][j];
A22[i][j] = A[i + newSize][j + newSize];
B11[i][j] = B[i][j];
B12[i][j] = B[i][j + newSize];
B21[i][j] = B[i + newSize][j];
B22[i][j] = B[i + newSize][j + newSize];
}
}
Matrix M1 = strassen(add(A11, A22), add(B11, B22));
Matrix M2 = strassen(add(A21, A22), B11);
Matrix M3 = strassen(A11, subtract(B12, B22));
Matrix M4 = strassen(A22, subtract(B21, B11));
Matrix M5 = strassen(add(A11, A12), B22);
Matrix M6 = strassen(subtract(A21, A11), add(B11, B12));
Matrix M7 = strassen(subtract(A12, A22), add(B21, B22));
Matrix C(n, vector<int>(n));
for (int i = 0; i < newSize; ++i) {
for (int j = 0; j < newSize; ++j) {
C[i][j] = M1[i][j] + M4[i][j] - M5[i][j] + M7[i][j];
C[i][j + newSize] = M3[i][j] + M5[i][j];
C[i + newSize][j] = M2[i][j] + M4[i][j];
C[i + newSize][j + newSize] = M1[i][j] - M2[i][j] + M3[i][j] + M6[i][j];
}
}
return C;
}
// 测试Strassen算法
int main() {
Matrix A = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
Matrix B = {{16, 15, 14, 13}, {12, 11, 10, 9}, {8, 7, 6, 5}, {4, 3, 2, 1}};
Matrix C = strassen(A, B);
cout << "Result matrix C:" << endl;
for (auto row : C) {
for (auto elem : row) {
cout << elem << " ";
}
cout << endl;
}
return 0;
}
代码说明
add和subtract函数用于矩阵的加减运算。strassen函数实现Strassen算法的递归分治。main函数用于测试矩阵乘法并打印结果。
Strassen算法适合较大规模的矩阵,能够显著提高计算效率。

评价
- 从实用的角度看,Strassen算法并不是解决矩阵乘法的最好选择:
(1)隐藏在Strassen算法运行时间Θ(nlog7)中的常数因子比直接过程的Θ(n3)的常数因子大。
(2)对于稀疏矩阵,有更快的专用算法可用。
(3)Strassen算法的数值稳定性不如直接过程,其计算过程中引起的误差积累比直接过程大。
(4)递归过程生成的子矩阵会消耗更多的存储空间。 - 目前已知的n * n矩阵乘的最优时间是Ο(n^2.376)(oppersmith-Winograd算法)



