万老师C语言笔记:二维数组：八皇后 幻方 迷宫问题

一、数组知识回顾

一维数组

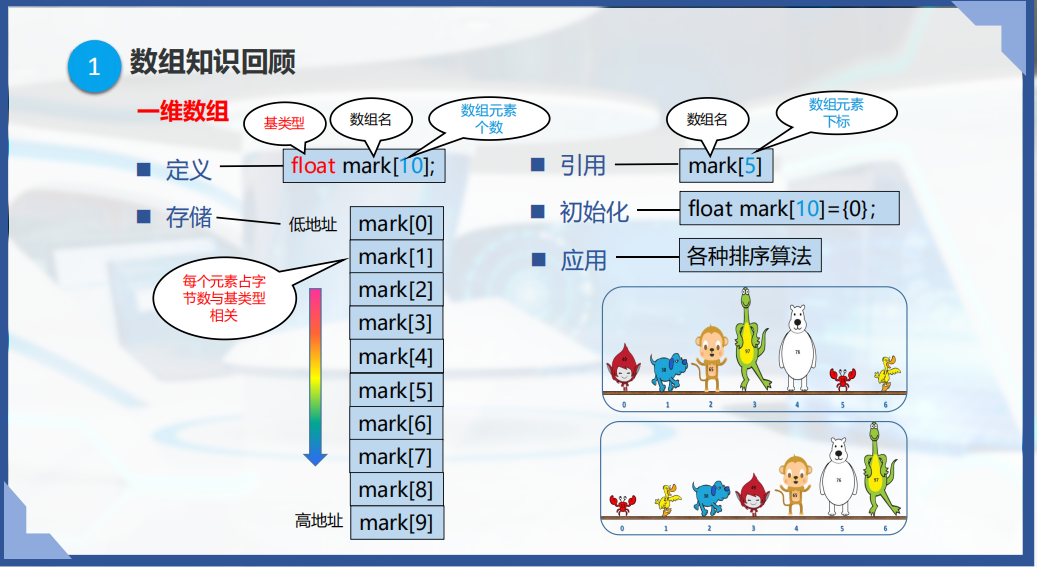
二维数组

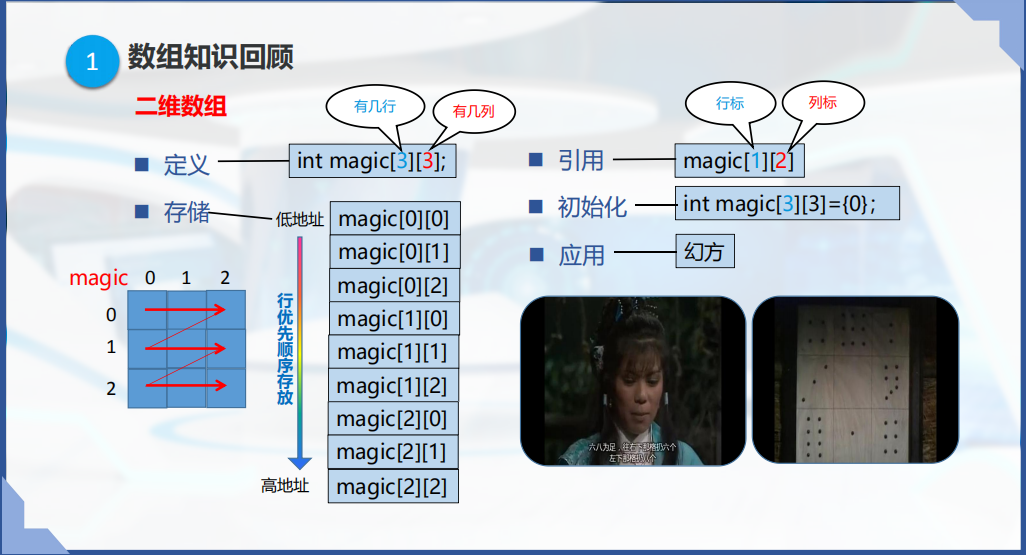
二、八皇后问题

八皇后问题是国际西洋棋棋手马克 斯·贝瑟尔于1848年提出： 在8×8格的国际象棋上摆放八个皇 后，使其不能互相攻击，即任意两个皇 后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。
高斯认为有76种方案。1854年在柏林的 象棋杂志上不同的作者发表了40种不同的解 ，后来有人用图论的方法解出92种结果。 计算机发明后，有多种计算机语言可以 解决此问题。

数据结构：二维数组？一维数组？

方案一：二维数组

用一个8行8列的二维数组存储8*8的国际 象棋棋盘，数组元素初值为0；0-代表没有放皇后 1-代表放置了皇后。
int board[MAX_N][MAX_N];
例如：
chess[0][5]=1;//在第0行第5列放一个皇后
chess[1][1]=1;//在第1行第1列放一个皇后

方案二：一维数组

用下标代表行，值代表列。只要数组每个值各不相同，就说明不在同一行和列，从而简化了冲突的判断，只需要考虑是否对角线冲突。

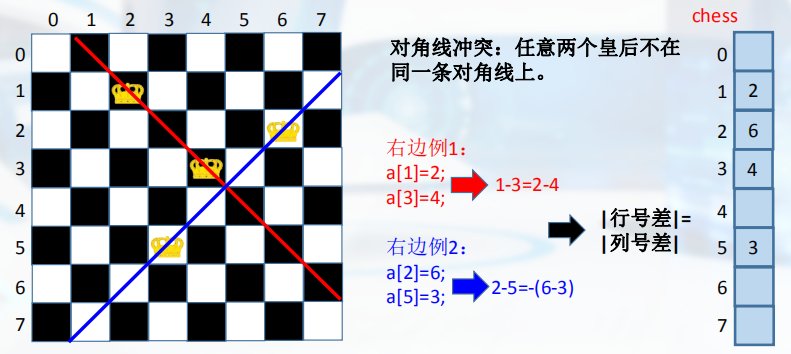
实际上等价于行号差与列号差的绝对值相同。因此可这样进行冲突检测：
if (queen[i] == col || abs(queen[i] - col) == abs(i - row))
那么如何摆放呢？

三、枚举方法

最适合计算机也一定不会遗漏任何一种摆放的方法！摆放方式共有：8×8 ×8 ×8 ×8 ×8 ×8 ×8 = 8^8
用八层for循环枚举。
分析：同一列没有必要再摆放，若第n个皇后与前面冲突，则不用进行n+1个皇后的摆放，而应回到上一步。（回溯思想）

    void queen() {
    int chess[8], i; // chess数组存放皇后的摆放，i用于输出皇后的循环变量

    for (chess[0] = 0; chess[0] <= 7; chess[0]++) // 对应第0行的8种摆放
        for (chess[1] = 0; chess[1] <= 7; chess[1]++)
            for (chess[2] = 0; chess[2] <= 7; chess[2]++)
                for (chess[3] = 0; chess[3] <= 7; chess[3]++)
                    for (chess[4] = 0; chess[4] <= 7; chess[4]++)
                        for (chess[5] = 0; chess[5] <= 7; chess[5]++)
                            for (chess[6] = 0; chess[6] <= 7; chess[6]++)
                                for (chess[7] = 0; chess[7] <= 7; chess[7]++)
                                    if (check(chess, 8) == 1) // 如果不存在冲突则输出这种摆放方案
                                        for (i = 0; i < 8; i++) // 输出每一行皇后的位置
                                            printf("%d ", chess[i]);}

这段代码通过嵌套的循环尝试所有可能的皇后摆放方式。对于每种摆放方式，它调用名为 check 的函数，检查是否存在皇后之间的冲突（即是否存在在同一行、同一列或对角线上）。如果没有冲突，它就打印出每一行皇后的位置。

四、回溯方法

    void queen() {
    int chess[8], i; // chess存放皇后的摆放 i用于输出皇后的循环变量

    // 循环尝试每一行的摆放方式
    for (chess[0] = 0; chess[0] <= 7; chess[0]++) {
        // 对应第0行的8种摆放
        for (chess[1] = 0; chess[1] <= 7; chess[1]++) {
            // 如果存在冲突，则看下一种摆放
            if (check(chess, 2) == 0)
                continue;
            else
                // 循环尝试第2行的摆放方式
                for (chess[2] = 0; chess[2] <= 7; chess[2]++) {
                    // 如果存在冲突，则看下一种摆放
                    if (check(chess, 3) == 0)
                        continue;
                    else
                        // 循环尝试第3行的摆放方式
                        // ... （以此类推，一直到第7行）
                        for (chess[7] = 0; chess[7] <= 7; chess[7]++) {
                            // 如果第8个皇后和前面7个冲突则看下一种摆放，否则输出这种摆放方式
                            if (check(chess, 8) == 0)
                                continue;
                            else
                                // 输出当前的摆放方式
                                for (i = 0; i <= 7; i++)
                                    print(chess[i]);
                        }
                }
        }
    }
    }
    // 函数check用于检查当前皇后的摆放是否与前面的皇后有冲突
    int check(int a[], int n) {
    // 实现检查的逻辑，如果有冲突返回0，否则返回1}

    // 函数print用于输出当前皇后的摆放
    void print(int queenPosition) {
    // 输出当前皇后的位置}

八重for循环 只能解决8皇后，如果变成N皇后呢？
有一种思路：
放下第1个皇后，还需要放下N-1个皇后；
放下第2个皇后，还需要放下N-2个皇后；
放下了第N个皇后，结束了(递归出口)
递归的回溯算法分析：实际上是一个DFS算法

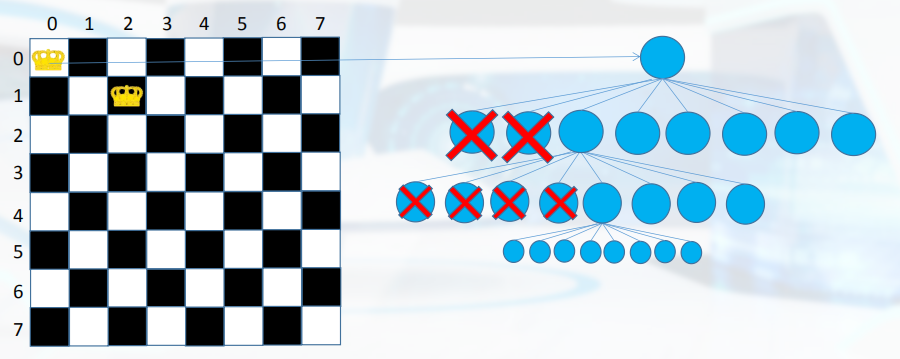
最终代码（一维数组实现）:

    #include <stdio.h>
    #include<math.h>
    #define N 4
    int queen[N];
    bool isSafe(int row, int col) {
    // 检查同一列是否有皇后
    for (int i = 0; i < row; i++) {
        if (queen[i] == col || abs(queen[i] - col) == abs(i - row)) {
            return false;
        }
    }
    return true;}

    int placeQueen(int row) {
    int count = 0;
    if (row == N) {
        // 所有皇后都已经放置，找到一个解法       
        return 1;
    }

    for (int col = 0; col < N; col++) {
        if (isSafe(row, col)) {
            // 在当前位置放置皇后
            queen[row] = col;
            // 递归放置下一行的皇后
            count+=placeQueen(row + 1);
            
        }
    }
    return count;}
    int main()
    {
    int count=placeQueen(0);
    printf("%d", count);
    return 0;
    }

五、幻方问题

幻方是指将若干个自然数排成纵横各为若干个数的正方形，使在同一行、同一列和同一对角线上的几个数的和都相等。此时我们只考虑奇幻方问题。可见：洛谷P2615
简单来说就是将1放在第一行的中间，下一个数放在上一个数“右上角”，若已被占，放在正下方。
例如，三阶幻方为：
8 1 6
3 5 7
4 9 2
/代码实现/

#include<stdio.h>
int n, a[40][40], x, y;
 int main() {
scanf("%d", &n);
x = 1, y = (n + 1) / 2;
for (int i = 1; i <= n * n; i++) {
	a[x][y] = i;
	if (!a[(x - 2 + n) % n + 1][y % n + 1])
		{
			x = (x - 2 + n) % n + 1, y = y % n + 1;
		}
	else x = x % n + 1;//数学运算
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			printf("%d ", a[i][j]);
		}
		printf("\n");
	}
    }

以下是if法题解，采用了动态内存分配。

#include <stdio.h> 
#include <stdlib.h>

int main()
    {
    int n;
    scanf("%d", &n);

    if (n <= 0)
    {
        printf("错误的输入。请输入一个正整数。");
        return 1;
    }

    int** a = (int**)malloc(sizeof(int*) * n);
    if (a == NULL)
    {
        printf("内存分配失败");
        return 1;
    }

    for (int i = 0; i < n; i++)
    {
        a[i] = (int*)malloc(sizeof(int) * n);
        if (a[i] == NULL)
        {
            printf("内存分配失败");
            return 1;
        }
    }
    int i = 0;
    int j = (n - 1) / 2;
    a[i][j] = 1;
    for (int k = 2; k <= n * n; k++)
    {
        if (i == 0 && j != n - 1)
        {
            i = n - 1;
            j++;
        }
        else if (i != 0 && j == n - 1)
        {
            i--;
            j = 0;
        }
        else if (i == 0 && j == n - 1)
        {
            i++;
        }
        else if (i != 0 && j != n - 1)
        {
            if (i-1>=0&&i-1<n&&j+1>=0&&j<n&&(!(a[i - 1][j + 1] >= 1 && a[i - 1][j + 1] <= n * n)))
            {
                i--;
                j++;
            }
            else
            {
                i++;
            }
        }
        a[i][j] = k;
    }

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            printf("%d ", a[i][j]);
        }
        printf("\n");
    }

    for (int i = 0; i < n; i++)
    {
        free(a[i]);
    }
    free(a);

    return 0;}

六、迷宫问题

迷宫问题显然无法用一维数组解决，因为同一行不只有一个“皇后”。采用DFS思想，先试探一个方向，若走不通，再返回上一步试探其它方向。