基础知识系列5--五大查找（二叉查找树代码未写）

从这一篇开始要介绍算法中的查找技术了。查找在我们生活中无处不在，比如查公交，查机票，查酒店。。。这些都是查找。

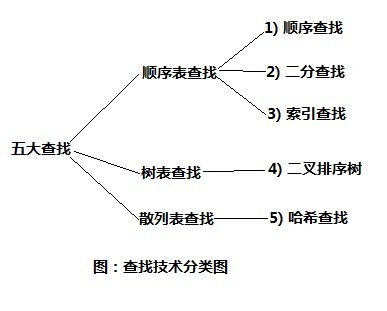
首先来看一下查找技术的分类。如下图：

 

1.顺序查找（Sequential Search）

那么这篇要总结的是顺序表中的顺序查找技术。

什么是顺序查找呢？顺序查找的原理很简单，就是遍历整个列表，逐个进行记录的关键字与给定值比较，若某个记录的关键字和给定值相等，则查找成功，找到所查的记录。如果直到最后一个记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找失败。

 

2.二分查找(Binary Search)

二分查找也属于顺序表查找范围，二分查找也称为折半查找。二分查找(有序)的时间复杂度为O(LogN)。

那么什么是二分查找呢？二分查找的基本思想是， 在有序表中，取中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；若给定值小于中间记录的关键字，则在中间记录的左半区继续查找；若给定值大于中间记录的关键字，则在中间记录的右半区继续查找。不断重复上述过程，直到找到为止。

从二分查找的定义我们可以看出，使用二分查找有两个前提条件：

1，待查找的列表必须有序。

2，必须使用线性表的顺序存储结构来存储数据。

 

代码实现

#include <stdio.h>

#define MAXSIZE 10
#define OK       0
#define ERROR   -1

typedef int Status;
typedef struct
{
    int data[MAXSIZE];
    int length;
}SeqList;
//
int BinarySearch(SeqList *q,int key)
{
    int low = 0;    //下限
    int high = q->length-1;    //上限

    while(low<=high)    //
    {
        int middle = (low+high)/2;
        if(q->data[middle] == key)    //判断是否等于关键字
        {
            return middle;
        }
        else
        {
            if(q->data[middle] > key)
                high = middle-1;
            else
                low = middle+1;
        }
    }
    printf("Not find %d\n",key);
    return ERROR; 
}

void Display(SeqList* q)
{
    int i;
    printf("SeqList:");
    for(i=0;i<q->length;i++)
        printf("%d ",q->data[i]);
    printf("\n");
}

int main(void)
{
    int i,j;
    SeqList q;
    
    for(i=0;i<MAXSIZE;i++)
        q.data[i] = i;
    q.length = MAXSIZE;

    Display(&q);
    
    printf("4 in the list is num :%d\n",BinarySearch(&q,4));
    BinarySearch(&q,10);
    return 0;
}

运行结果

 

3.索引查找

这一篇我们要总结的是索引查找，关于索引，我们很容易地联想到数据库中的索引，建立了索引，可以大大提高数据库的查询速度。

索引查找又称为分块查找，是一种介于顺序查找和二分查找之间的一种查找方法，分块查找的基本思想是：首先查找索引表，可用二分查找或顺序查找，然后在确定的块中进行顺序查找。

分块查找的时间复杂度为O(√n)。

在实现索引查找算法前需要弄清楚以下三个术语。

1，主表。即要查找的对象。

2，索引项。一般我们会将主表分成几个子表，每个子表建立一个索引，这个索引就叫索引项。

3，索引表。即索引项的集合。

同时，索引项包括以下三点。

1，index，即索引指向主表的关键字。

2，start，即index在主表中的位置。

3，length，即子表的区间长度。

 

4.二叉排序树(Binary Sort Tree)

这一篇开始总结的是二叉排序树。构造一棵二叉排序树的目的，其实并不是为了排序，而是为了提高查找和插入删除的效率。

那么什么是二叉排序树呢？二叉排序树具有以下几个特点。

1，若根节点有左子树，则左子树的所有节点都比根节点小。

2，若根节点有右子树，则右子树的所有节点都比根节点大。

3，根节点的左，右子树也分别为二叉排序树。

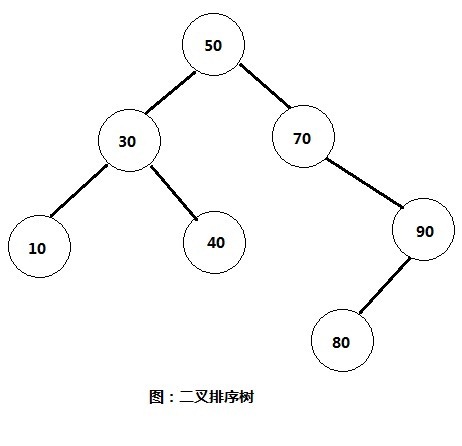
下面是二叉排序树的图示，通过图可以加深对二叉排序树的理解。

下面是二叉排序树常见的操作及思路。

1，插入节点

思路：比如我们要插入数字20到这棵二叉排序树中。那么步骤如下：

1) 首先将20与根节点进行比较，发现比根节点小，所以继续与根节点的左子树30比较。

2) 发现20比30也要小，所以继续与30的左子树10进行比较。

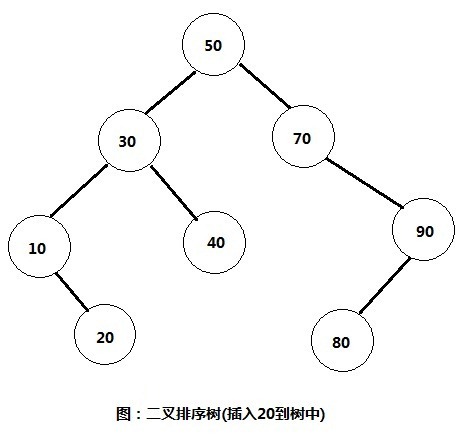
3) 发现20比10要大，所以就将20插入到10的右子树中。

此时二叉排序树效果如图：

2，查找节点

比如我们要查找节点10，那么思路如下：

1) 还是一样，首先将10与根节点50进行比较大小，发现比根节点要小，所以继续与根节点的左子树30进行比较。

2) 发现10比左子树30要小，所以继续与30的左子树10进行比较。

3) 发现两值相等，即查找成功，返回10的位置。

过程与插入相同，这里就不贴图了。

3，删除节点

删除节点的情况相对复杂，主要分以下三种情形：

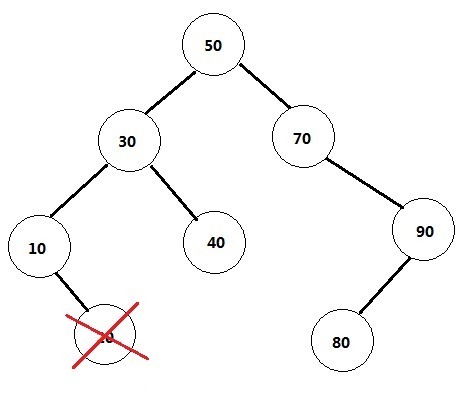
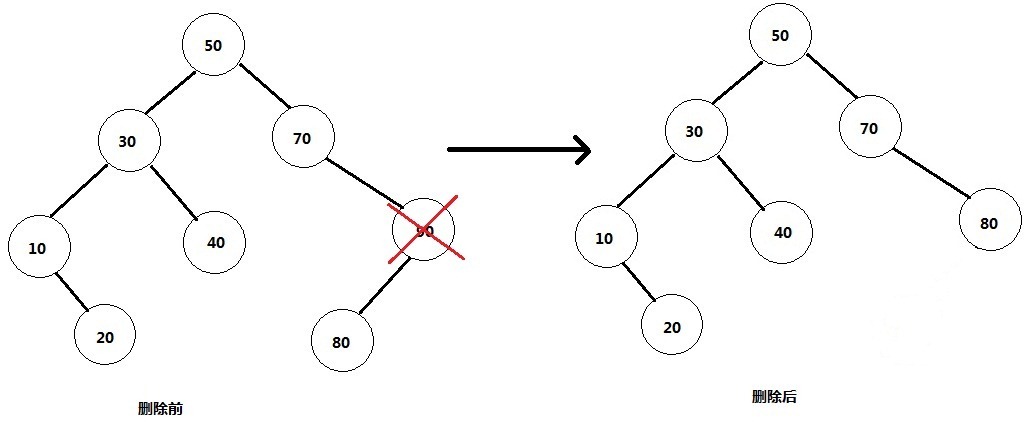
1) 删除的是叶节点(即没有孩子节点的)。比如20，删除它不会破坏原来树的结构，最简单。如图所示。

2) 删除的是单孩子节点。比如90，删除它后需要将它的孩子节点与自己的父节点相连。情形比第一种复杂一些。

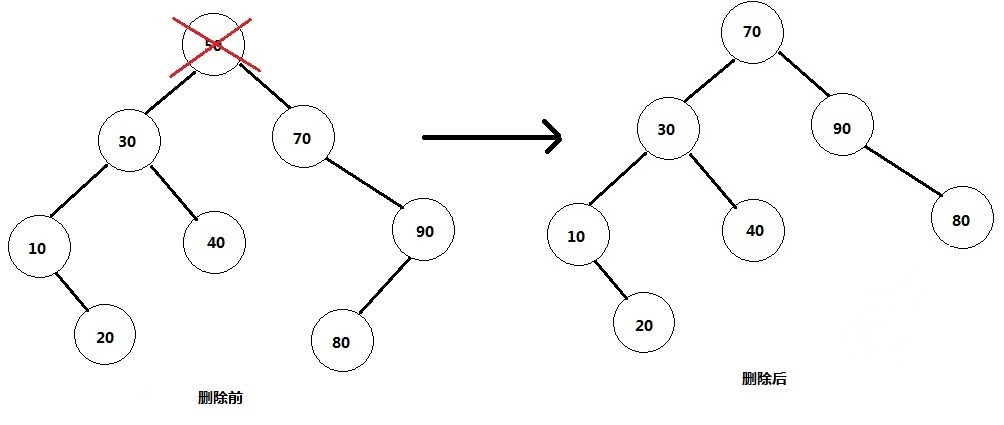
3) 删除的是有左右孩子的节点。比如根节点50，这里有一个问题就是删除它后将谁做为根节点的问题？利用二叉树的中序遍历，就是右节点的左子树的最左孩子。

分析完了，有了思路之后，下面就开始写代码来实现这些功能了。

 

5.哈希查找(Hash)

这一篇要总结的是五大查找的最后一篇，哈希查找，也称为散列查找(本文以哈希称呼)。提起哈希，我的第一印象就是C#中的Hashtable类，它是由一组key/value的键值对组成的集合，它就是应用了散列技术。

那么，什么是哈希查找呢？在弄清楚什么是哈希查找之前，我们要弄清楚哈希技术，哈希技术是在记录的存储位置和记录的关键字之间建立一个确定的对应关系f，使得每个关键字key对应一个存储位置f(key)。查找时，根据这个确定的对应关系找到给定值的映射f(key),若查找集合中存在这个记录，则必定在f(key)的位置上。哈希技术既是一种存储方法，也是一种查找方法。

哈希表的基本原理请看下面的链接：

哈希查找因何快？我们使用它需要付出什么代价

 

六种哈希函数的构造方法：

1，直接定址法：

函数公式：f(key)=a*key+b (a,b为常数)

这种方法的优点是：简单，均匀，不会产生冲突。但是需要事先知道关键字的分布情况，适合查找表较小并且连续的情况。

2，数字分析法：

比如我们的11位手机号码“136XXXX7887”，其中前三位是接入号，一般对应不同运营公司的子品牌，如130是联通如意通，136是移动神州行，153是电信等。中间四们是HLR识别号，表示用户归属地。最后四们才是真正的用户号。

若我们现在要存储某家公司员工登记表，如果用手机号码作为关键字，那么极有可能前7位都是相同的，所以我们选择后面的四们作为哈希地址就是不错的选择。

3，平方取中法：

故名思义，比如关键字是1234，那么它的平方就是1522756，再抽取中间的3位就是227作为哈希地址。

4，折叠法：

折叠法是将关键字从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些)，然后将这几部分叠加求和，并按哈希表表长，取后几位作为哈希地址。

比如我们的关键字是9876543210，哈希表表长三位，我们将它分为四组，987|654|321|0 ，然后将它们叠加求和987+654+321+0=1962，再求后3位即得到哈希地址为962，哈哈，是不是很有意思。

5，除留余数法：

函数公式：f(key)=key mod p (p<=m)m为哈希表表长。

这种方法是最常用的哈希函数构造方法。

6，随机数法：

函数公式：f(key)= random(key)。

这里random是随机函数，当关键字的长度不等是，采用这种方法比较合适。

 

hash是如何处理冲突的?

两种哈希函数冲突解决方法：

我们设计得最好的哈希函数也不可能完全避免冲突，当我们在使用哈希函数后发现两个关键字key1!=key2，但是却有f(key1)=f(key2)，即发生冲突。

方法一：开放定址法：

开放定址法就是一旦发生了冲突，就去寻找下一个空的哈希地址，只要哈希表足够大，空的哈希地址总是能找到，然后将记录插入。这种方法是最常用的解决冲突的方法。

方法二：链地址法：

将哈希值相同的数据元素存放在一个链表中，在查找哈希表的过程中，当查找到这个链表时，必须采用线性查找方法。

 

下面是实现代码：

#include "stdio.h"
#include "stdlib.h"

#define OK     0
#define ERROR -1

#define HASHSIZE 7　　//定义散列表长为数组的长度
#define NULLKEY -32768

typedef int Status;
typedef struct
{
    int *elem;　　//数据元素存储地址，动态分配数组
    int count;　　//当前数据元素个数
}HashTable;

int m = 0;　　//散列表表长

Status Init(HashTable *hashTable)
{
    int i;
    
    m = HASHSIZE;
    hashTable->elem = (int*)malloc(m*sizeof(int));　　//申请内存
    hashTable->count = m;
    for(i=0;i<m;i++)
    {
        hashTable->elem[i] = NULLKEY;
    } 

    return OK;
}
/*哈希函数-除留余数法*/
int Hash(int data)
{
    return data%m;
}

void Insert(HashTable *hashTable,int data)
{
    int hashAddress = Hash(data);　　//求哈希地址

    while(hashTable->elem[hashAddress] != NULLKEY)　　//发生冲突，利用开放地址的线性探测法解决冲突
        hashAddress = (++hashAddress)%m;

    hashTable->elem[hashAddress] = data;
}

int Search(HashTable *hashTable,int data)
{
    int hashAddress = Hash(data);
    
    while(hashTable->elem[hashAddress] != data)
    {
        hashAddress = (++hashAddress)%m;
        if(hashTable->elem[hashAddress] == NULLKEY || hashAddress == Hash(data))
            return ERROR;
    }
    
    return hashAddress;
}

void Display(HashTable *hashTable)
{
    int i;

    printf("哈希表为");
    for(i=0;i<hashTable->count;i++)
    {
        printf("%d ",hashTable->elem[i]);
    }
    printf("\n");
}

int main(void)
{
    int i,result;
    int j=21;
    HashTable hashTable;
    int arr[HASHSIZE] = {6,5,4,3,2,1,0};

    Init(&hashTable);
    
    for(i=0;i<HASHSIZE;i++)
        Insert(&hashTable,arr[i]);

    Display(&hashTable);

    for(j=0;j<=7;j++)
    {
        if((result = Search(&hashTable,j)) == -1)
            printf("%d is not exist in hash!\n",j);
        else
            printf("%d 在哈希表的位置是:%d\n",j,result);
    }
    
    return 0;
}

运行结果