雷达方程分析
雷达方程是设计雷达系统的基础。雷达方程如下:
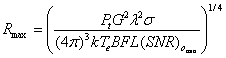
一般情况,雷达系统设计已知雷达需要探测距离R,所以雷达方程常进行变换应用,例如根据《雷达系统设计MATLAB仿真》中的:
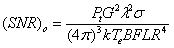
其中,G为天线增益,λ为波长,σ为目标截面积,Pt为峰值功率,k为玻尔兹曼常数,Te有效温度,B带宽,F噪声系数,L雷达损失。
研究最小可检测信噪比SNR和不同探测距离R之间的关系(关于目标截面积σ、峰值功率Pt)
function [ snr ] = radar_eq( pt,freq,G,sigma,Te,B,Nf,loss,range ) % 雷达方程 % pt 峰值功率 W % freq 雷达中心频率 Hz % G 天线增益 dB % sigma 目标截面积 m^2 % Te 有效噪声温度 K % B 带宽 Hz % Nf 噪声系数 dB % loss 雷达损失 dB % range 目标距离(单值或向量) m % snr SNR(单值或向量,根据输入距离) dB % c = 3.0e+8; %光速 lambda = c/freq; %波长 p_peak = 10*log10(pt); %将峰值功率转换成dB形式 lambda_sqdb = 10*log10(lambda^2); sigmadb = 10*log10(sigma); four_pi_cub = 10*log10((4.0*pi)^3); k_db = 10*log10(1.38e-23); %Boltzman常数转换成dB形式 Te_db = 10*log10(Te); B_db = 10*log10(B); range_pwr4_db = 10*log10(range.^4); % 根据雷达方程计算SNR值 num = p_peak + G + G + lambda_sqdb + sigmadb; den = four_pi_cub + k_db + Te_db + B_db + Nf + loss + range_pwr4_db; snr = num - den; return end
close all;
clear all;
pt = 1.5e+6; %峰值功率W
freq = 5.6e+9; %中心频率Hz
G = 45.0; %天线增益dB
sigma = 0.1; %目标截面积m^2
Te = 290.0; %有效噪声温度K
B = 5.0e+6; %带宽Hz
Nf = 3.0; %噪声系数dB
loss = 6.0; %雷达损失dB
range = linspace(25e3,165e3,1000); %均匀产生距离由25km至165km,1000个距离点
snr1 = radar_eq(pt,freq,G,sigma,Te,B,Nf,loss,range);
snr2 = radar_eq(pt,freq,G,sigma/10,Te,B,Nf,loss,range);
snr3 = radar_eq(pt,freq,G,sigma*10,Te,B,Nf,loss,range);
figure(1)
rangekm = range./1000;
plot(rangekm,snr3,'k',rangekm,snr1,'r-.',rangekm,snr2,'b:');
grid;
legend('\sigma = 0 dBsm','\sigma = -10dBsm','\sigma = -20 dBsm');
xlabel('检测距离 - Km');
ylabel('SNR - dB');
snr1 = radar_eq(pt,freq,G,sigma,Te,B,Nf,loss,range);
snr2 = radar_eq(pt*0.4,freq,G,sigma,Te,B,Nf,loss,range);
snr3 = radar_eq(pt*1.8,freq,G,sigma,Te,B,Nf,loss,range);
figure(2)
plot(rangekm,snr3,'k',rangekm,snr1,'r-.',rangekm,snr2,'b:');
grid;
legend('Pt = 2.16MW','Pt = 1.5MW','Pt = 0.6MW');
xlabel('检测距离 - Km');
ylabel('SNR - dB');
结果:
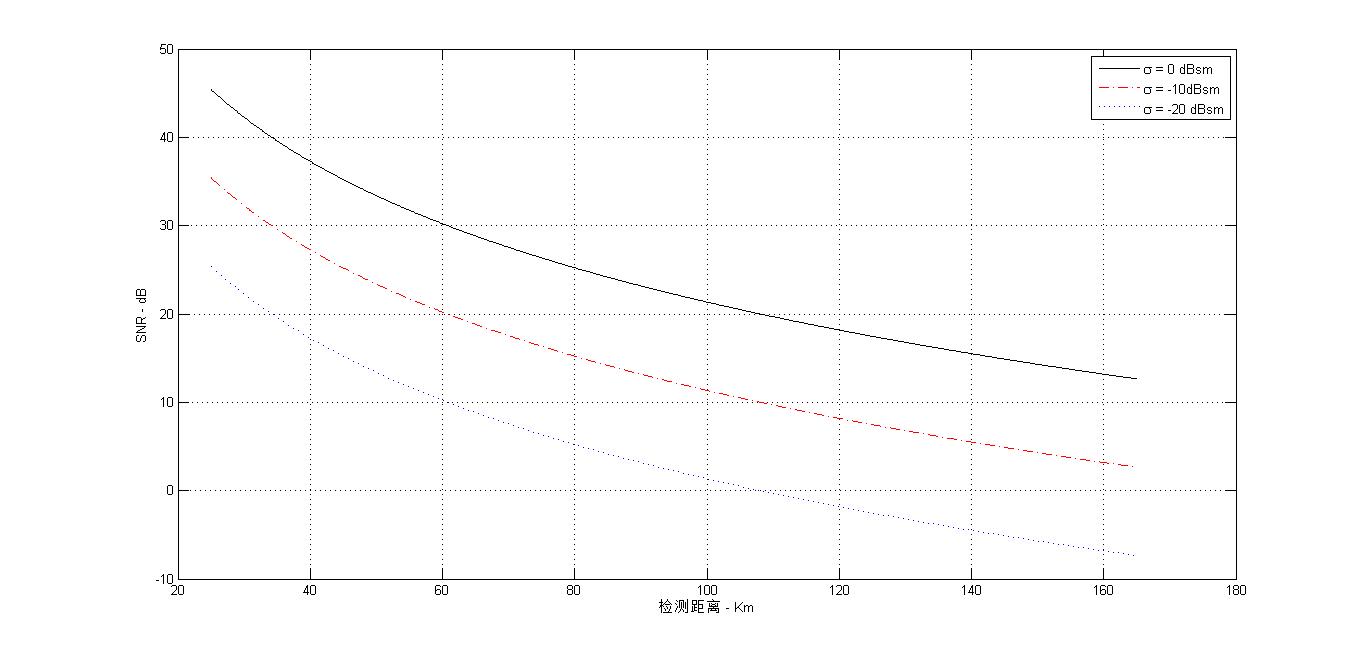
图1 最小可检测信噪比SNR和不同探测距离R之间的关系(关于目标截面积σ)
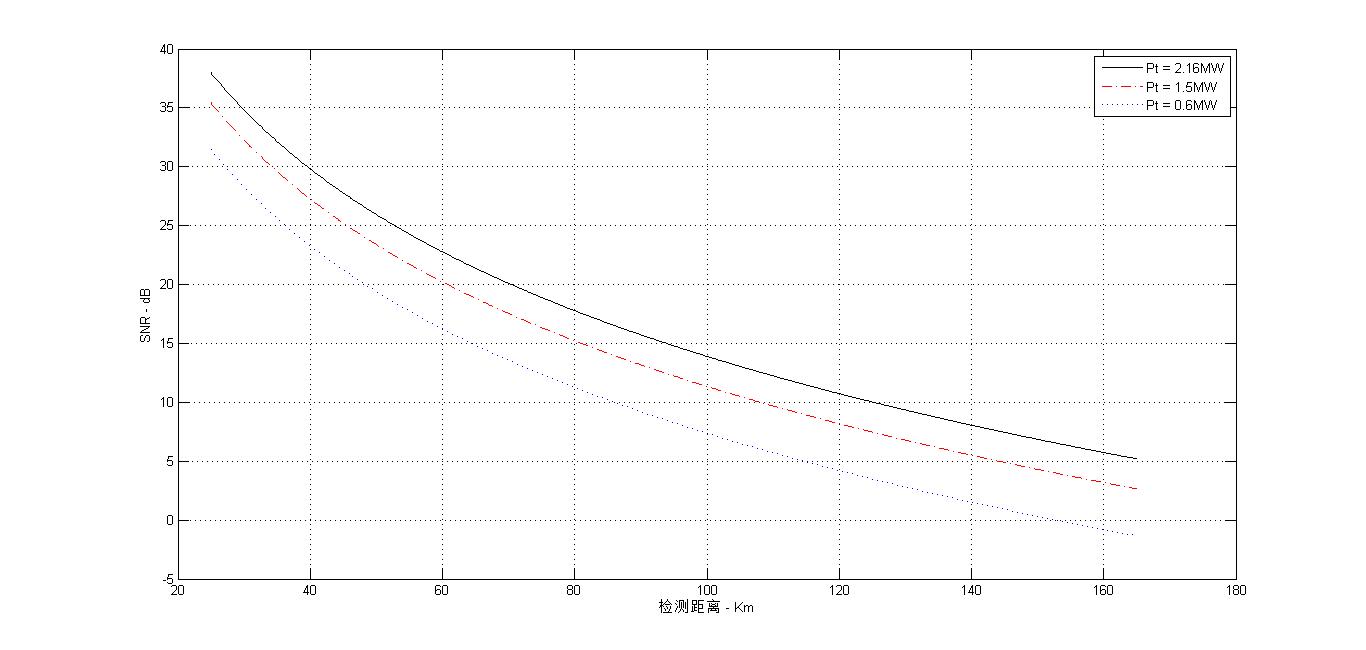
图2 最小可检测信噪比SNR和不同探测距离R之间的关系(峰值功率Pt)


