数据结构之树
一、树结构的定义
树是一种重要的非线性数据结构,其基于递归思想的定义为:
树是一种n(n>0)个点的有限集合,且有m(m>0)层,其中:1)当m=0时,有且只有一个特定的点称为根(root);2)当mmax>m>0时,每个点都有一个前驱和一个后继;3)当m=mmax时,每个点称为叶节点,只有一个前驱;4)由根节点到每个叶节点有且仅有一条路径。(如图所示是一棵树结构,其中A是根节点,C、D、F、H、I是叶子节点)
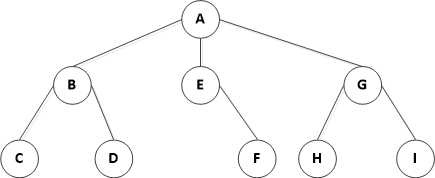
二、树结构的分类
树结构主要分为普通树和二叉树。本质意义上来讲,所有树都是普通树,二叉树(BST,binary search tree)是一种特殊的普通树结构。二叉树的定义:一个空的普通树或者包含一个根节点与一个左子树和一个右子树的树,且每个左子树与右子树都是一个二叉树。(如图所示是一棵二叉树。)
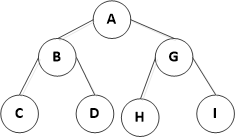
二叉树的分类:满二叉树、完全二叉树、完美平衡二叉树、不平衡二叉树。
满二叉树:1)除叶节点以外,每个节点都有两个后继;2)前一层有m个节点,则下一层必然有2m个节点。
完全二叉树:1)除了最后一层都是满二叉树;2)最后一层上的节点都是由左到右的填充。
完美平衡二叉树:1)除最后一层都是满二叉树;2)最后一层上的节点都是由右到左填充。
不平衡二叉树:除满二叉树,完全二叉树及完美二叉树之后的二叉树。
满二叉树的特性:1)如果二叉树的高度为H(如果只有一个根节点时,H=0),则共有N=2H+1-1个节点;2)如果有N个节点,则树的高度为H=log2(N+1)-1
三、二叉树的遍历
二叉树的遍历主要分为:前序遍历、中序遍历、后序遍历、及层序遍历
前序遍历:1)先访问根节点,然后遍历左子树,最后遍历右子树;2)每个子树的遍历过程也是遵循先根节点,然后左子树,最后右子树的顺序遍历。
中序遍历:1)先遍历左子树,然后访问根节点,最后遍历右子树;2)每个子树的遍历过程也是先遍历左子树,然后访问根节点,最后遍历右子树。
后序遍历:1)先遍历左子树,然后遍历右子树,最后访问根节点;2)每个子树的遍历过程也是先遍历左子树,然后遍历右子树,最后访问根节点。
层序遍历:从0层开始,逐层由左到右的访问每一个节点。


