math---线性代数の本质
一、线性空间
- 你有多个向量并且可以移除一个而不减小张成空间时,称为线性相关
- 在二维空间上,随便找两个向量(前提是不共线),则他俩可以张成整个平面
- 在三维空间,任意三个向量同理
二、矩阵线性变换与矩阵相乘
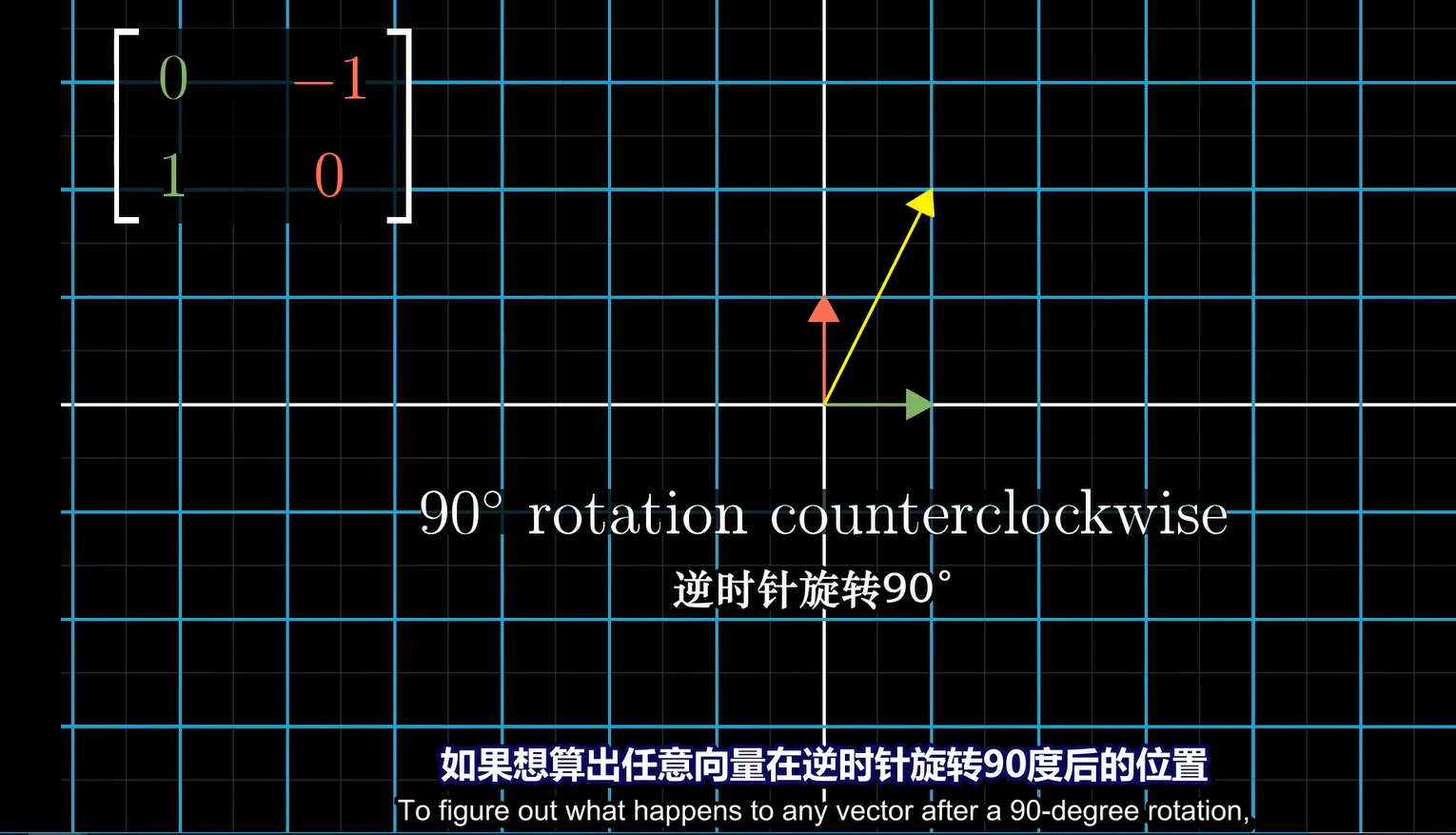
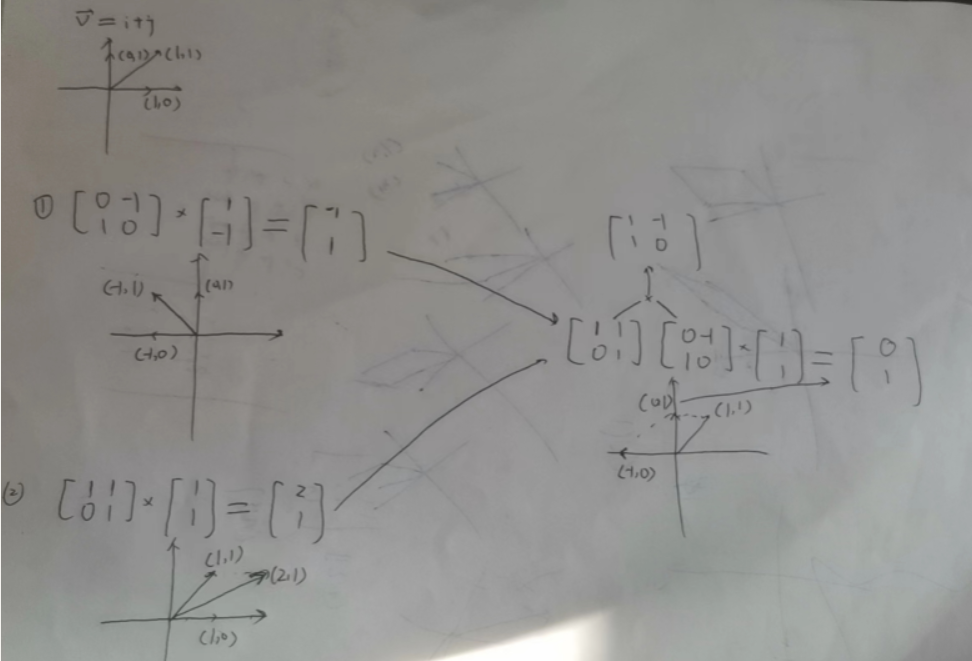
1、旋转
ai + bj ,其中
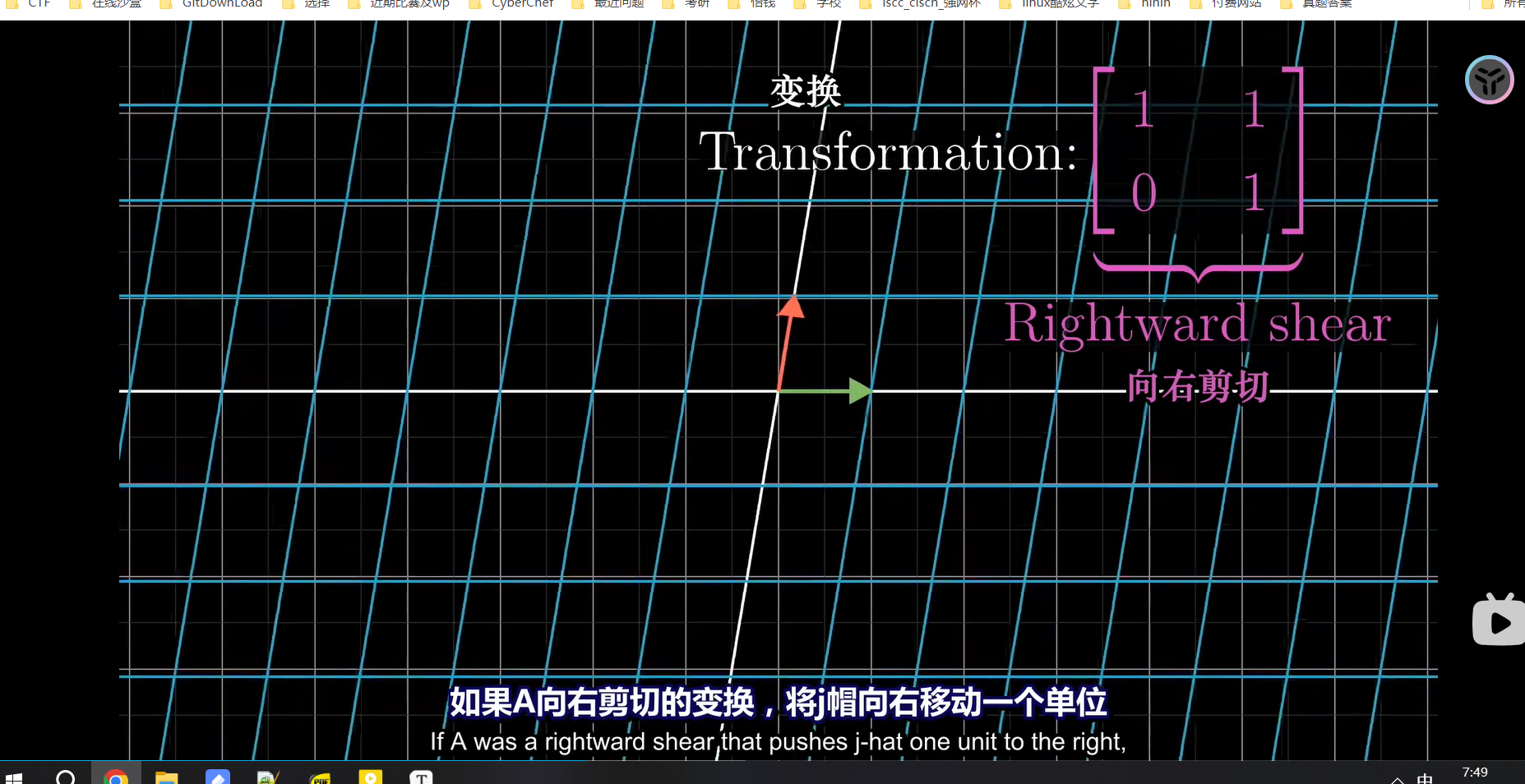
2、剪切/错切变换
i帽不变,j帽变
i+bj
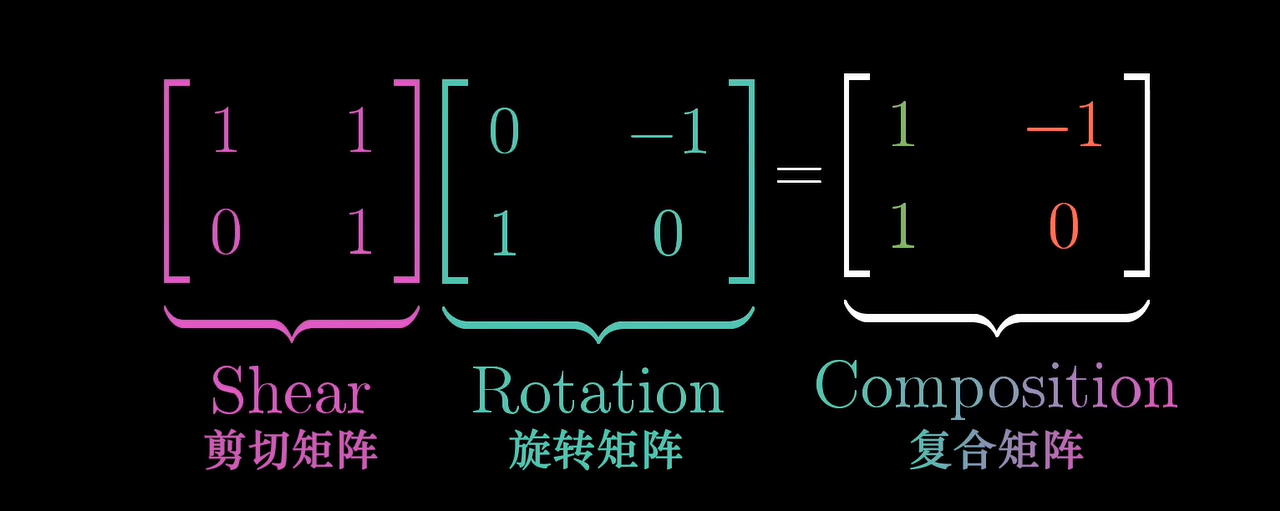
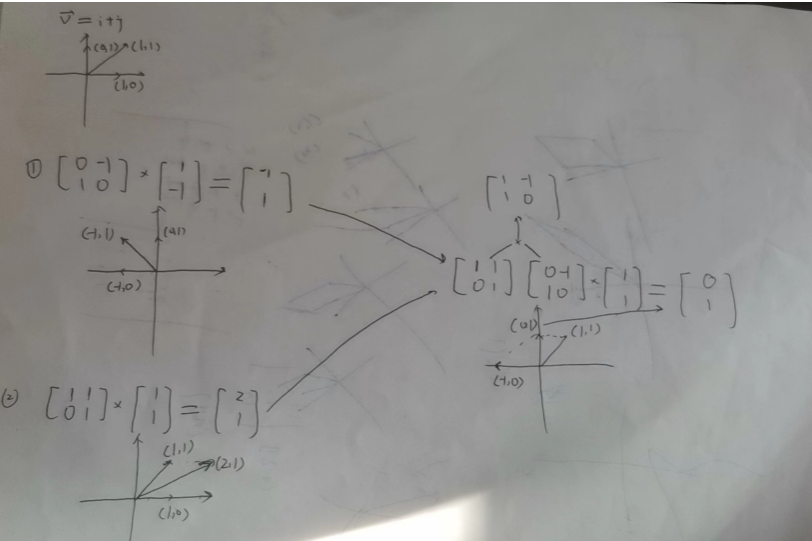
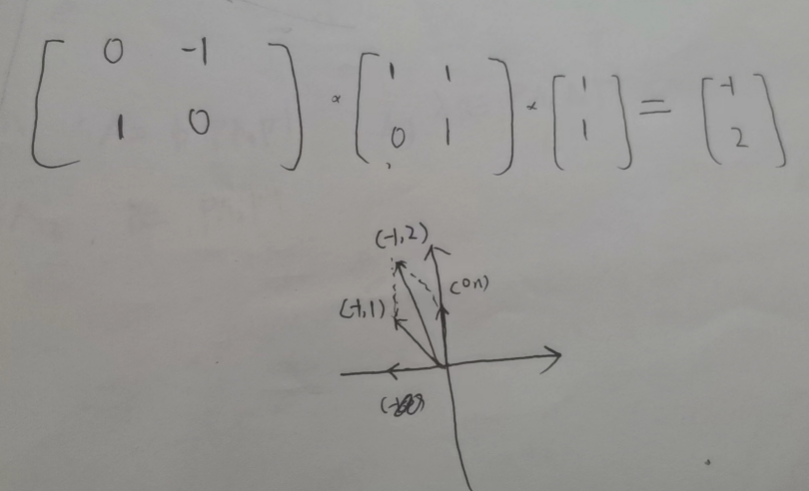
3、复合变换
ai+bj
随便取值
ps: 这个变换实际上都是基于直角坐标系的,两次变换都是基于直角坐标系
三、行列式
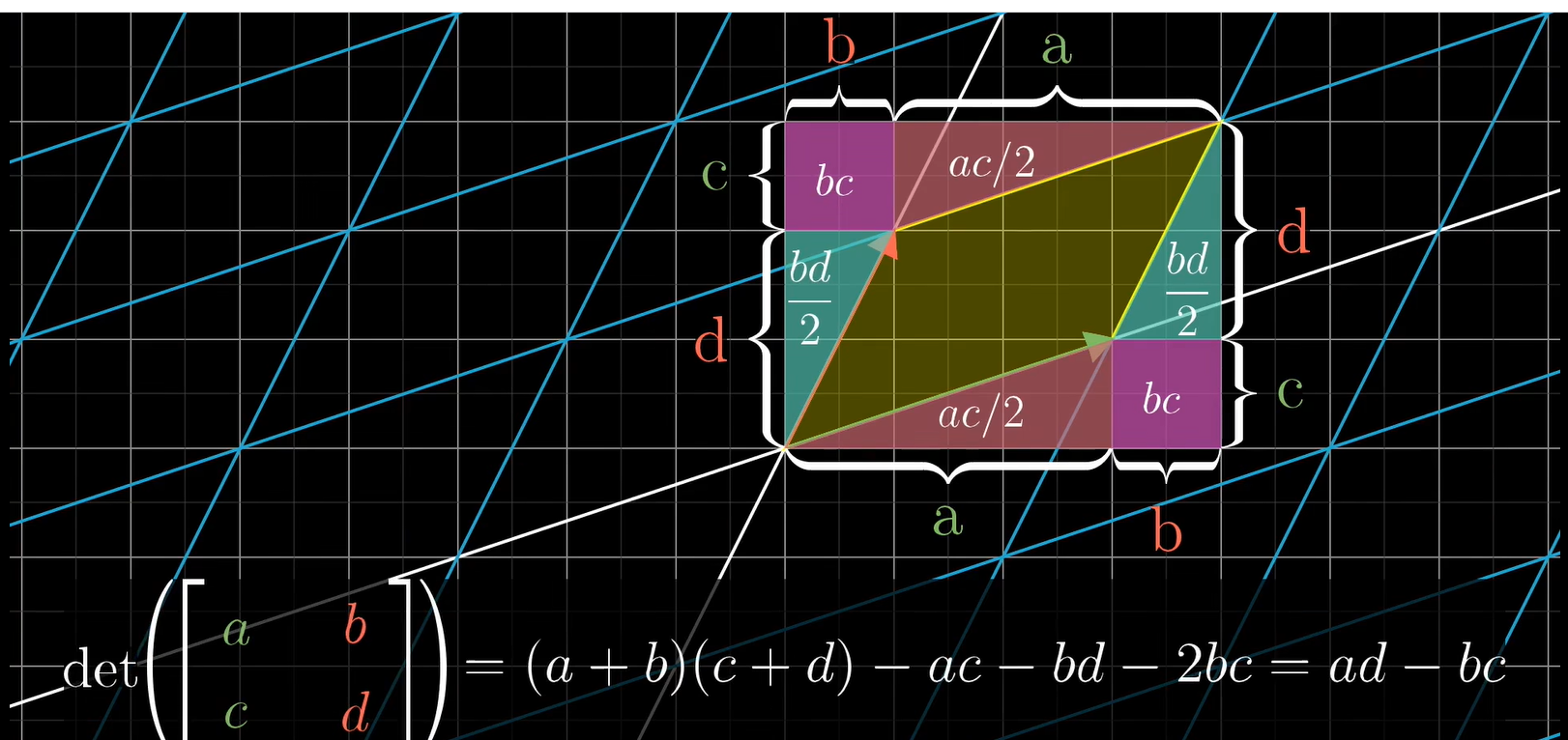
1、行列式是描述其对应矩阵张成区域变化倍数的关系
2、如果行列式为0,说明矩阵所代表的变换将空间压缩到更小的维度上
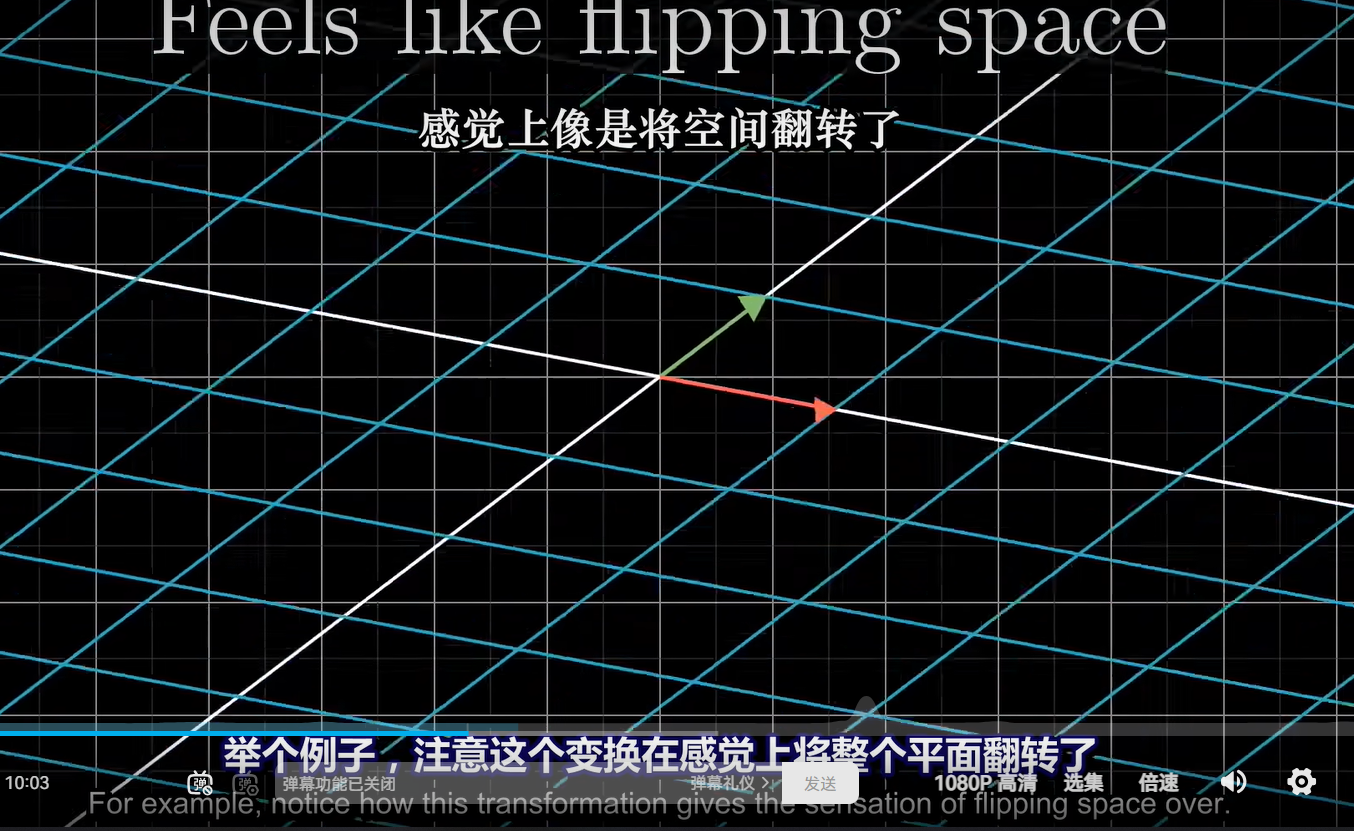
3、行列式为负,就说明该矩阵变换翻转了平面
或者说在二维面下时j在i的左边(一开始是在右边)
但是其绝对值还是决定着缩放的大小
三维下,行列式是平行六面体的体积,
行列式若为0,则说明,空间变换成了一个面或点
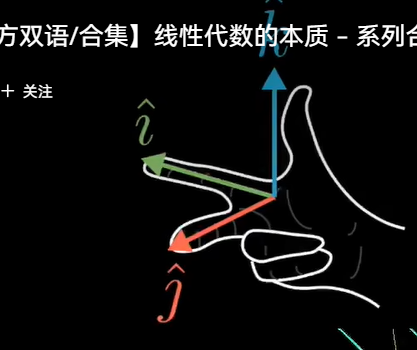
行列式为负,则说明不满足右手定理
复合变换,行列式的计算
对于行列式的相乘证明:
很显然,就是对M1缩放,M2缩放
四、逆矩阵、列空间、零空间
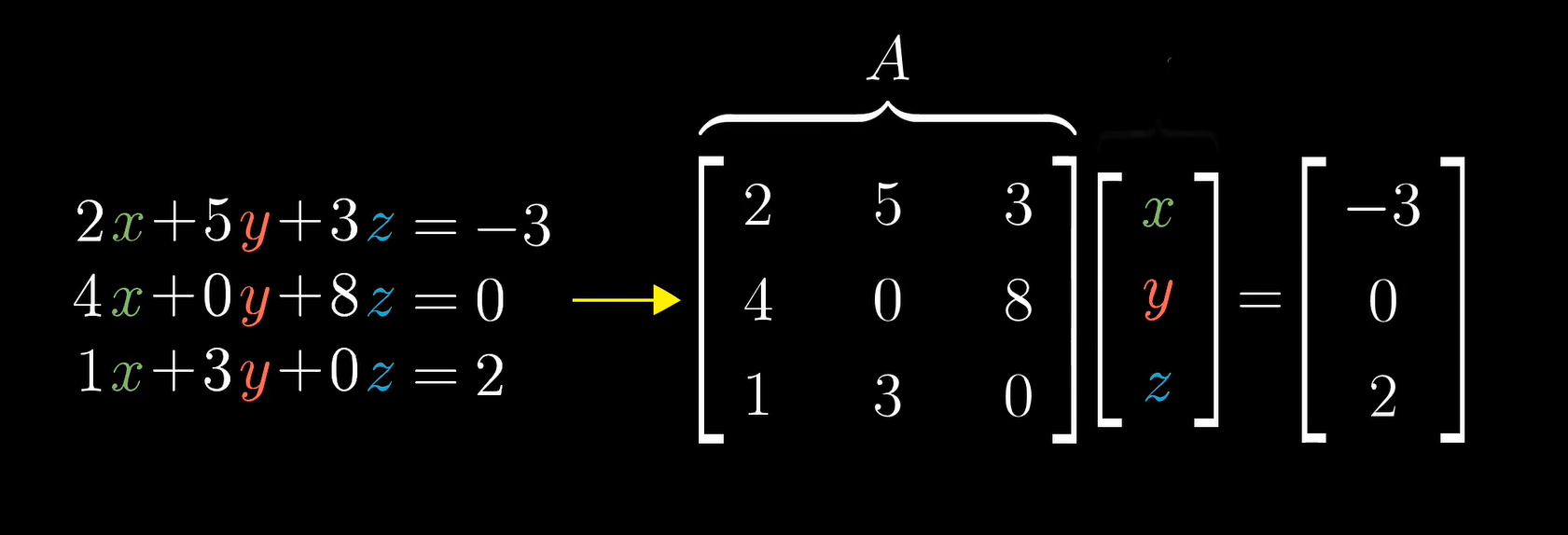
线性方程组
[x,y,z] 代表了所有能通过线性变换拟合到 向量 [-3,0,2]的向量
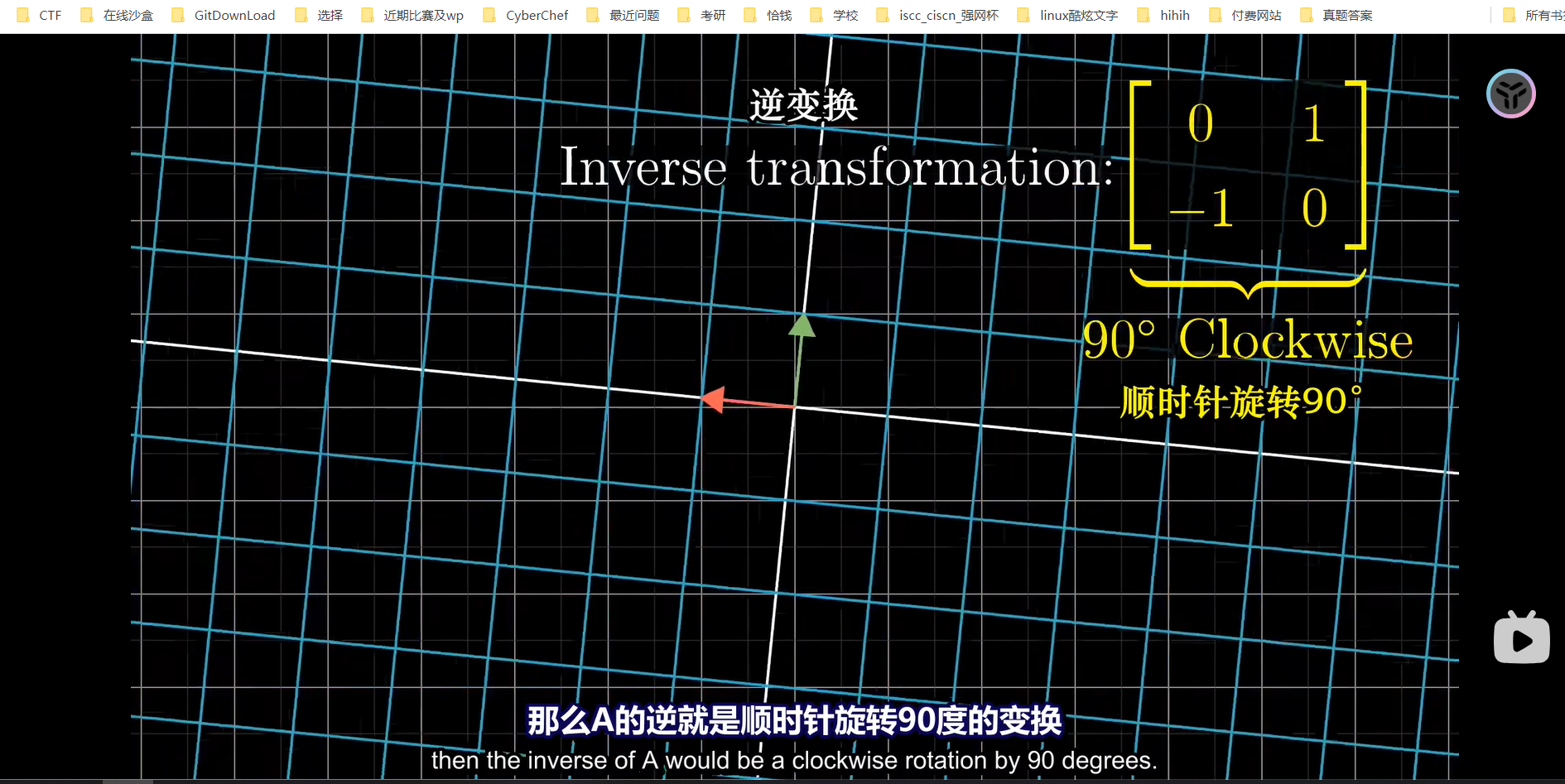
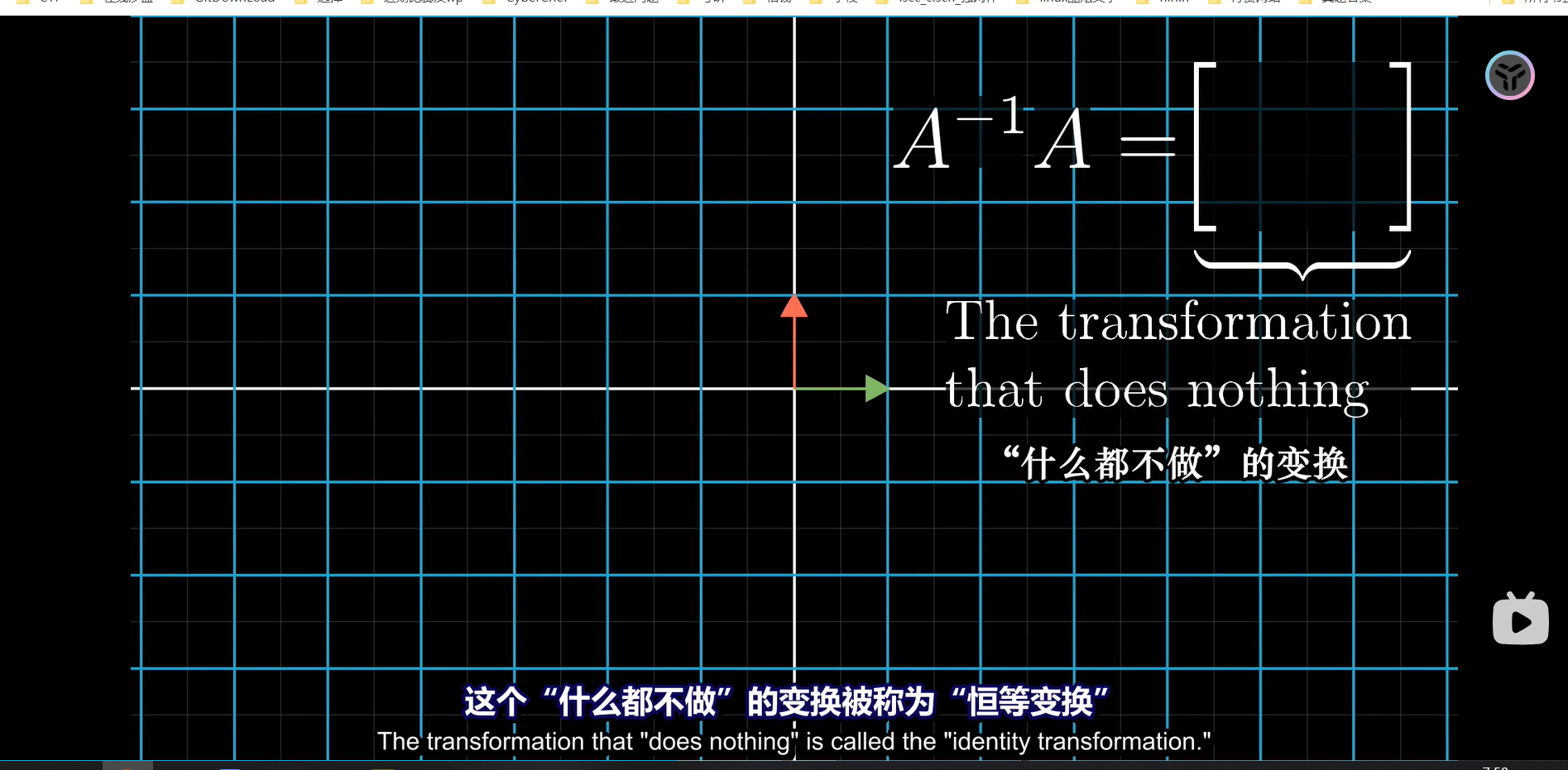
逆矩阵
列空间
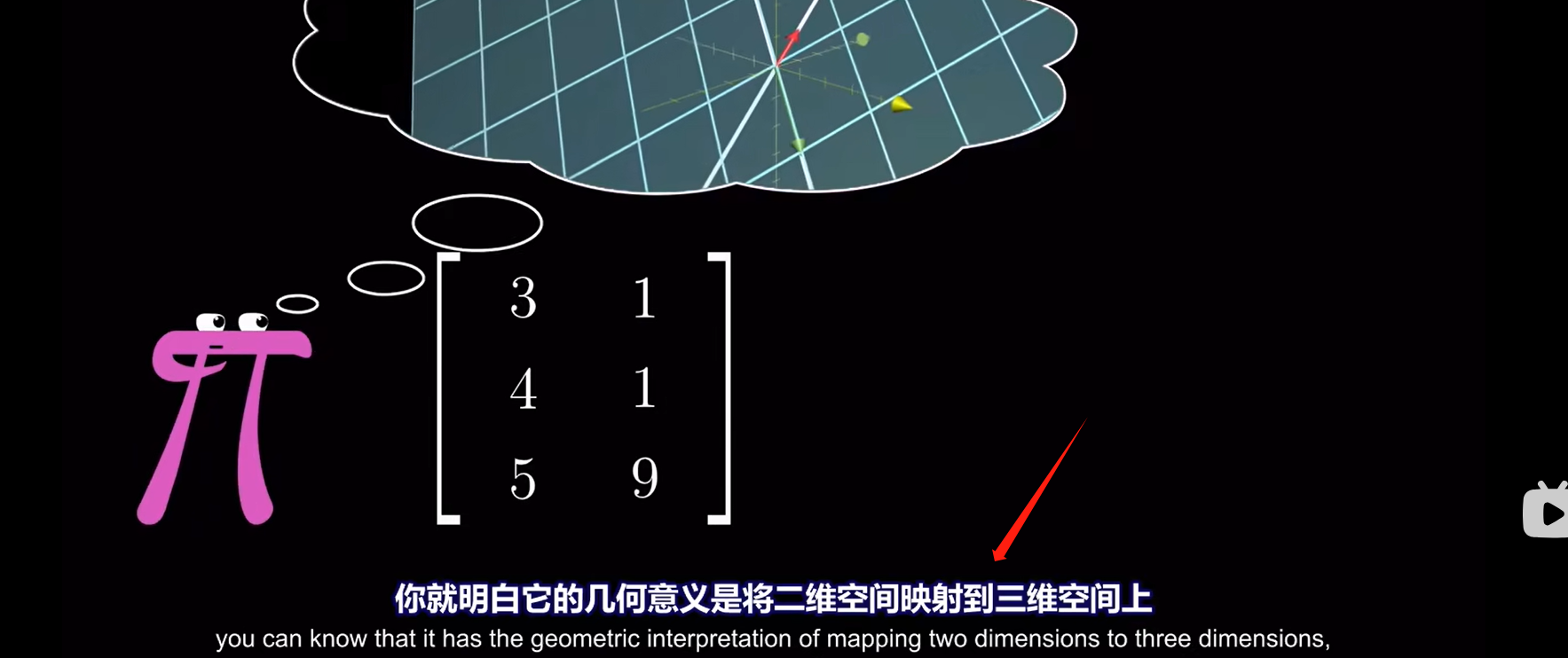
非方阵
五、点积和对偶性
对偶性:
在数学领域中,对偶一般来说是以一对一的方式,常常通过某个对合算子,把一种概念、公理或数学结构转化为另一种概念、公理或数学结构:如果A的对偶是B,那么B的对偶是A。由于对合有时候会存在不动点,因此A的对偶有时候会是A自身。
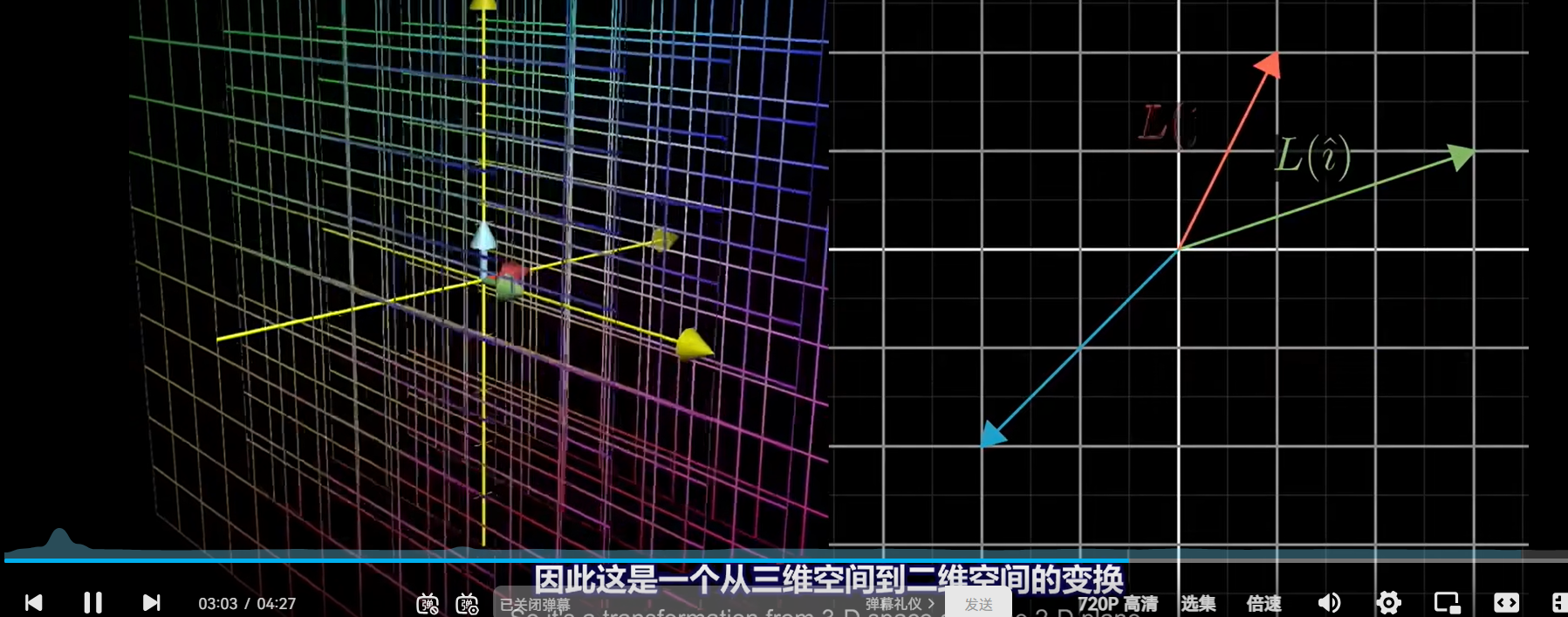
任何时候看到一个 2维映射为1维的向量,无论这个线性变换如何定义,在二维空间一定有一个向量与之相对应,这个就与“对偶性”相关
对于点积而言,向量仿佛是一个特定变换的概念性记号(把向量当成线性变换的一个载体)
因为它并不只数值的相加
六、叉积
叉积介绍
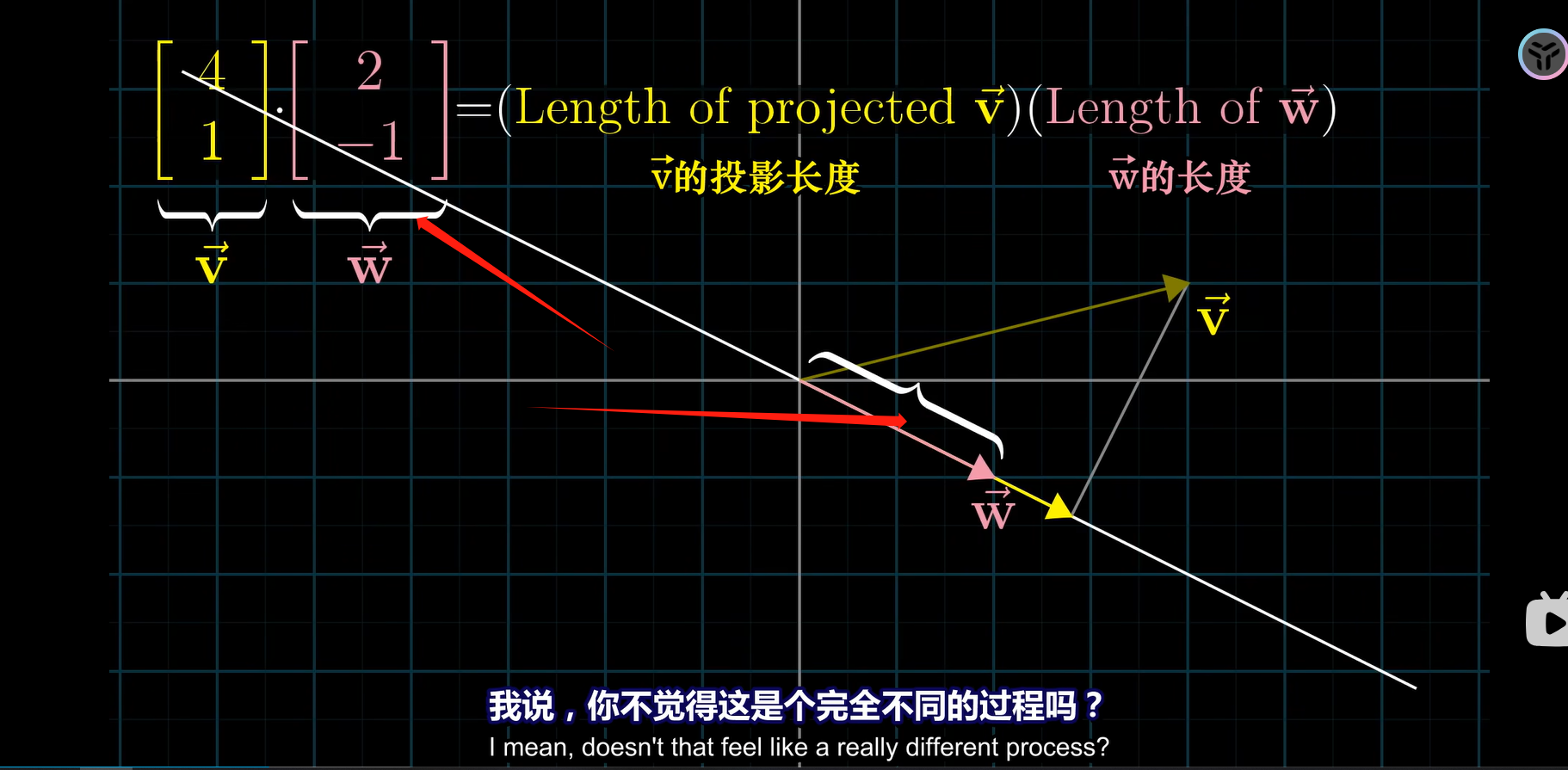
点乘,也叫数量积。结果是一个向量在另一个向量方向上投影的长度,是一个标量。
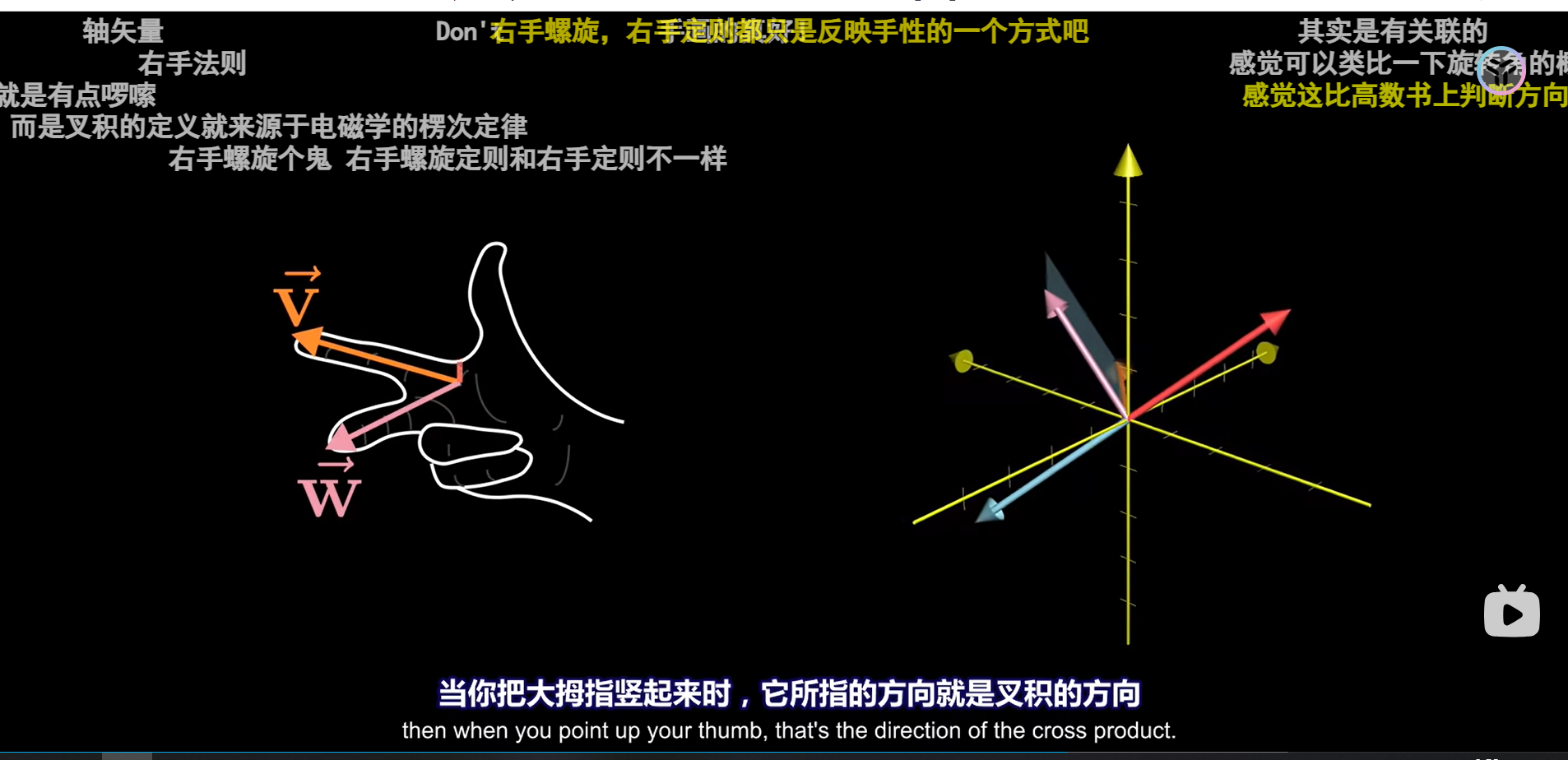
叉乘,也叫向量积。结果是一个和已有两个向量都垂直的向量
行列式的值就是叉乘的结果,行列式的一切运算性质可用于叉乘
真正的叉乘还要加上方向,比如
两个向量的叉积公式本来是这样的:
数值公式:
但为了计算方便,高数上给的两个向量的叉积的计算公式是这样:
和斯托克斯公式很像
空间向量的叉积计算原理---
前置知识
1、首先要明白a向量与b向量的叉积为c一定垂直于a,b两向量,并且在数值上等于a,b俩向量张成的平行四边形的面积,三维下同理
2、三个向量的叉乘等于一个平行六面体的体积
证明: 求 向量A(v1,v2,v3)与B(w1,w2,w3)的叉乘
- 首先引入 向量C(x,y,z),使其与A,B构成三维矩阵D,此矩阵的行列式等于该三个向量围城的平行六面体的体积
同时引入向量P(p1,p2,p3),使其点乘C,代表C(对偶于)从三维空间到一维空间的变换
- 此时发现D矩阵的行列式相当于以 A(v1,v2,v3)与B(w1,w2,w3)作为平行四边形的底,以C(x,y,z)关于A,B垂线的投影作为平行四边形的高
而对于左边的P·(x,y,z),p就只能是垂直于A,B的垂线,且数值大小等于A,B围城的平行四边形的面积,这与我们前面提到的前置知识相吻合,也就是说P就可以做A,B的叉积
七、基变换 (相似理论)
在坐标系之间对单个向量的描述进行相互转化
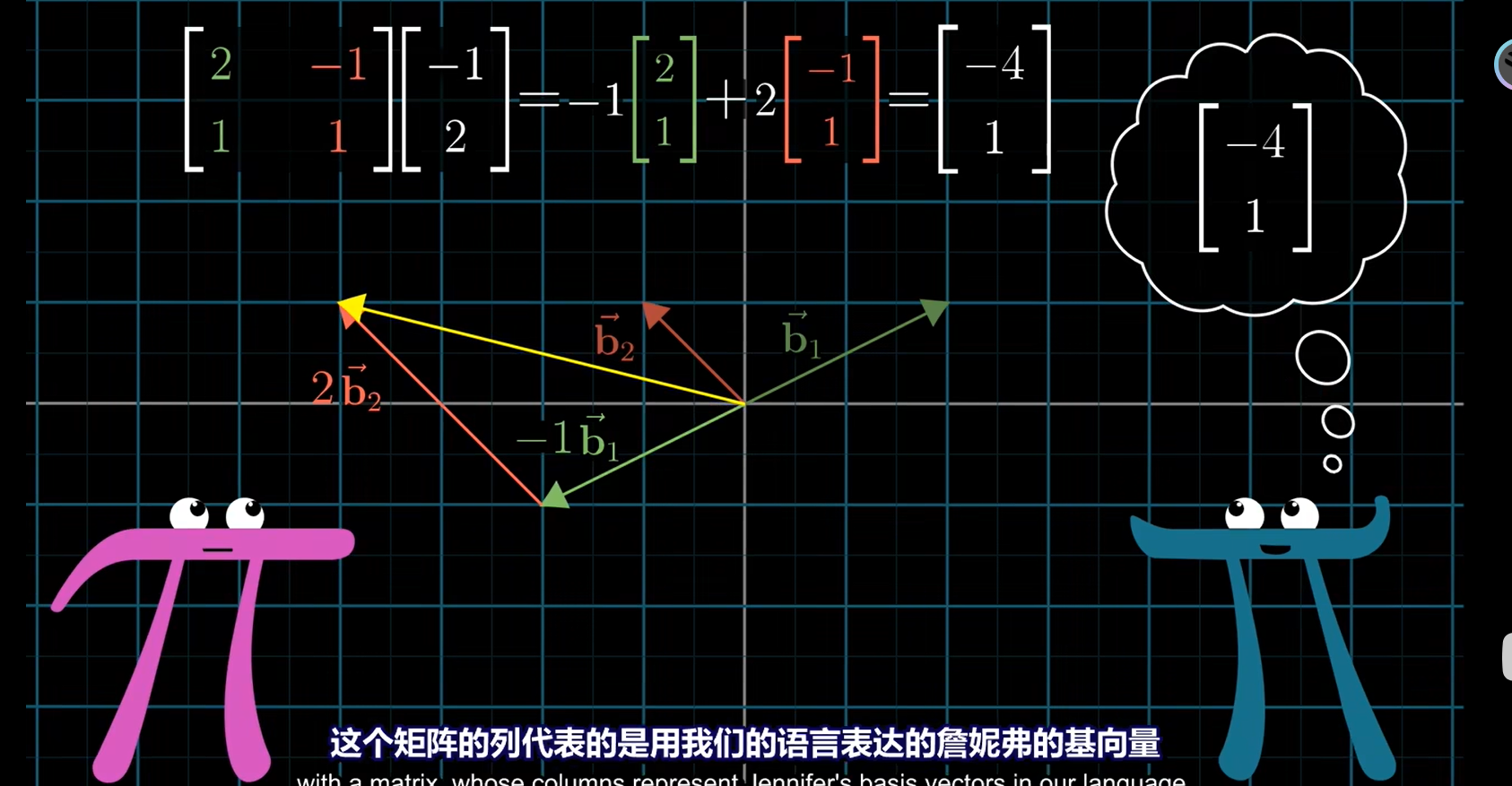
用我们的网络去表示她的向量
与矩阵相乘很像
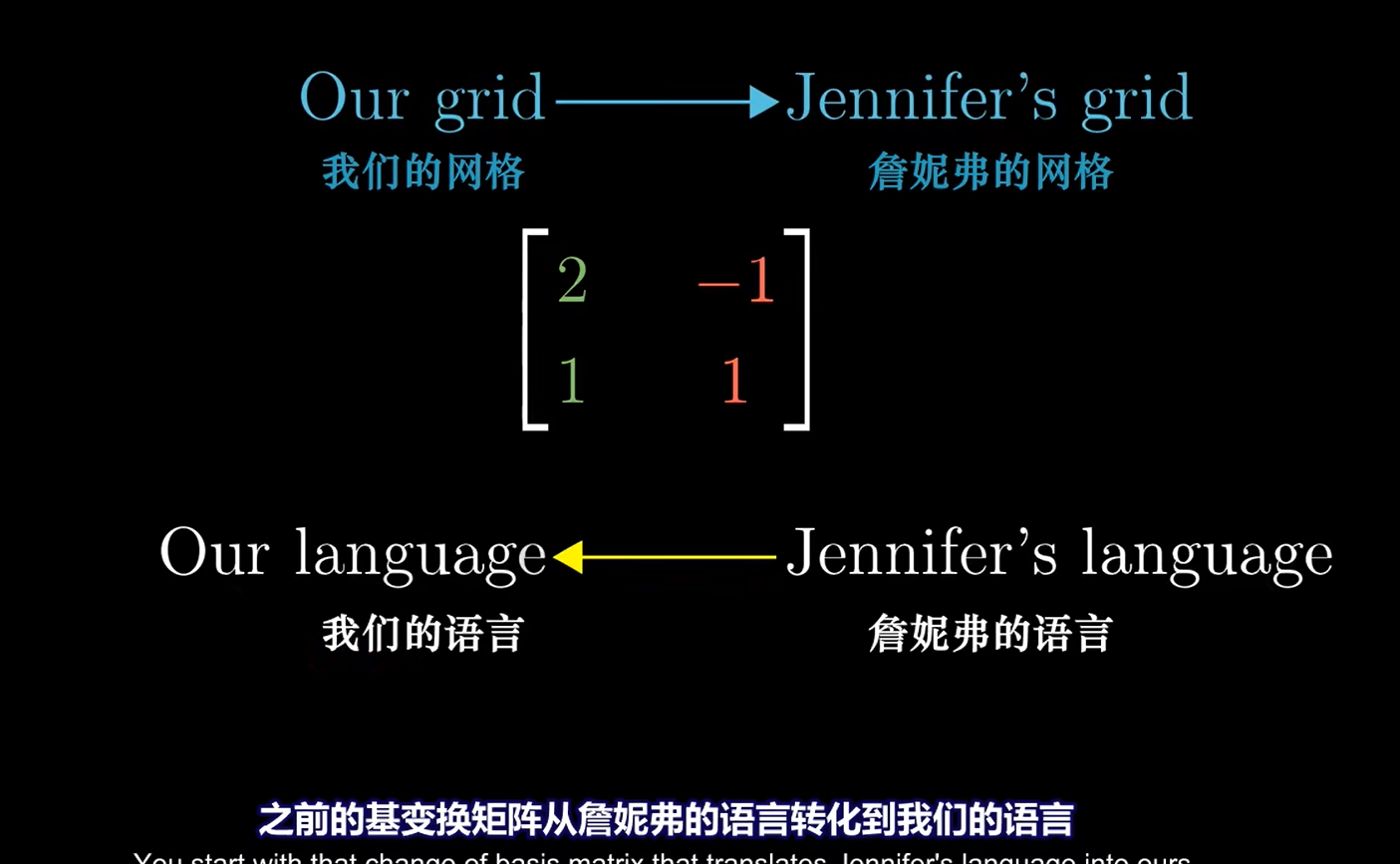
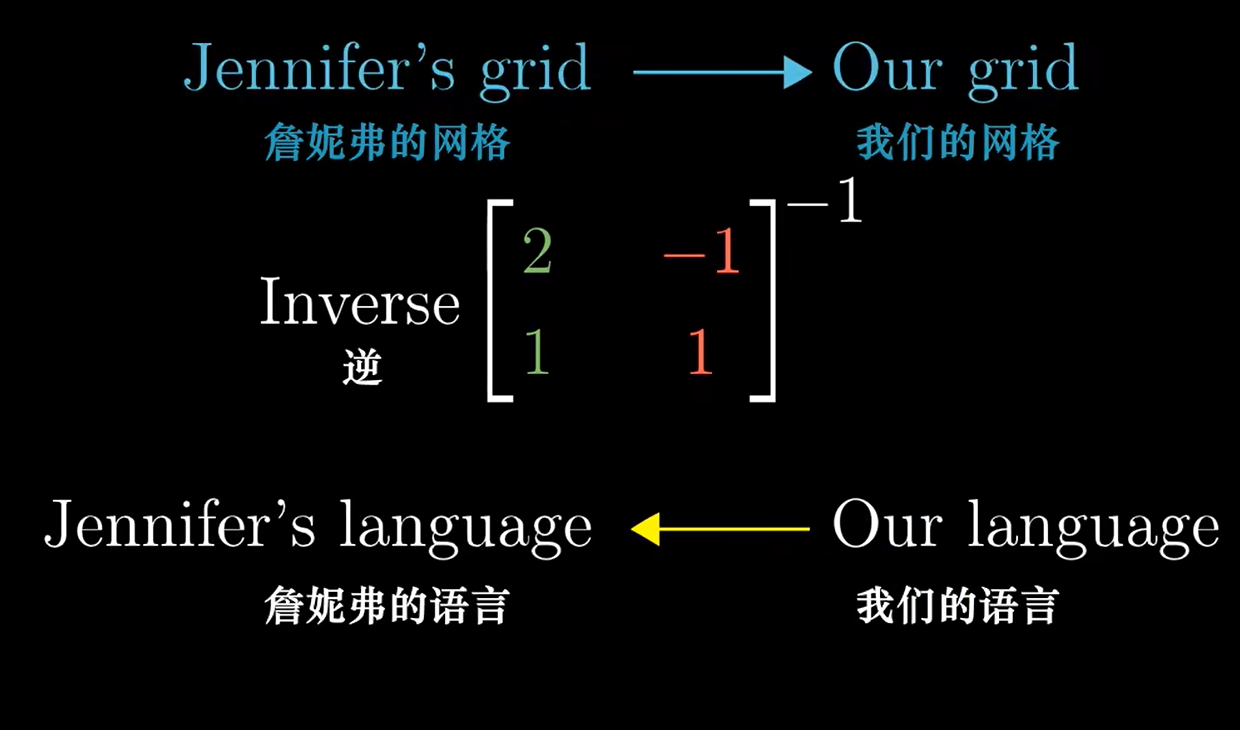
反过来:用她的网格表示我们的向量
需要取逆
之前:
之后:
记住都是左乘
用她的语言描述在其网格内变换的向量 (矩阵相似)
上面我们是用左乘矩阵的方式来得到她的向量在我们网格下的位置,或者我们的向量在她网格下的位置
下面我们要讲的是,她的矩阵经过线性变换后在她网格下的位置
比如,她的基为:H = ,其上有一向量S = ,我们想使该向量左旋90°,即X =
那么我们可以
-
先获得向量在我们基下的坐标: 即 H * S =>
-
将其在我们基下旋转90°:得到向量 SS =
-
再向量SS转化为在她的基下的向量:
即可得到最后的位置
前三个矩阵都是固定的,而第四个向量是可变的,转化一下可以得到一个固定类似公式的转化矩阵:
前三个矩阵的复合即为线性变化矩阵,它接收用詹妮弗语言描述的向量,并输出用詹妮弗语言描述的变换后的向量
这三个矩阵的结果设为 ,她的基设为P,线性变换(左旋90°)设为A
即有
代表在她坐标系下旋转90°的情况
A代表在我们坐标系下旋转90°的情况,这俩是相似的!!!
八、特征值与特征向量 (相似对角化)
特征值与特征向量的引出
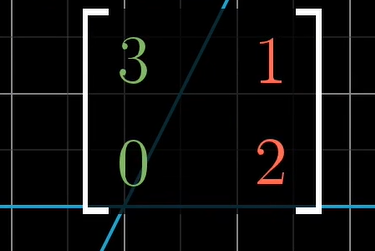
对于一个基变换:
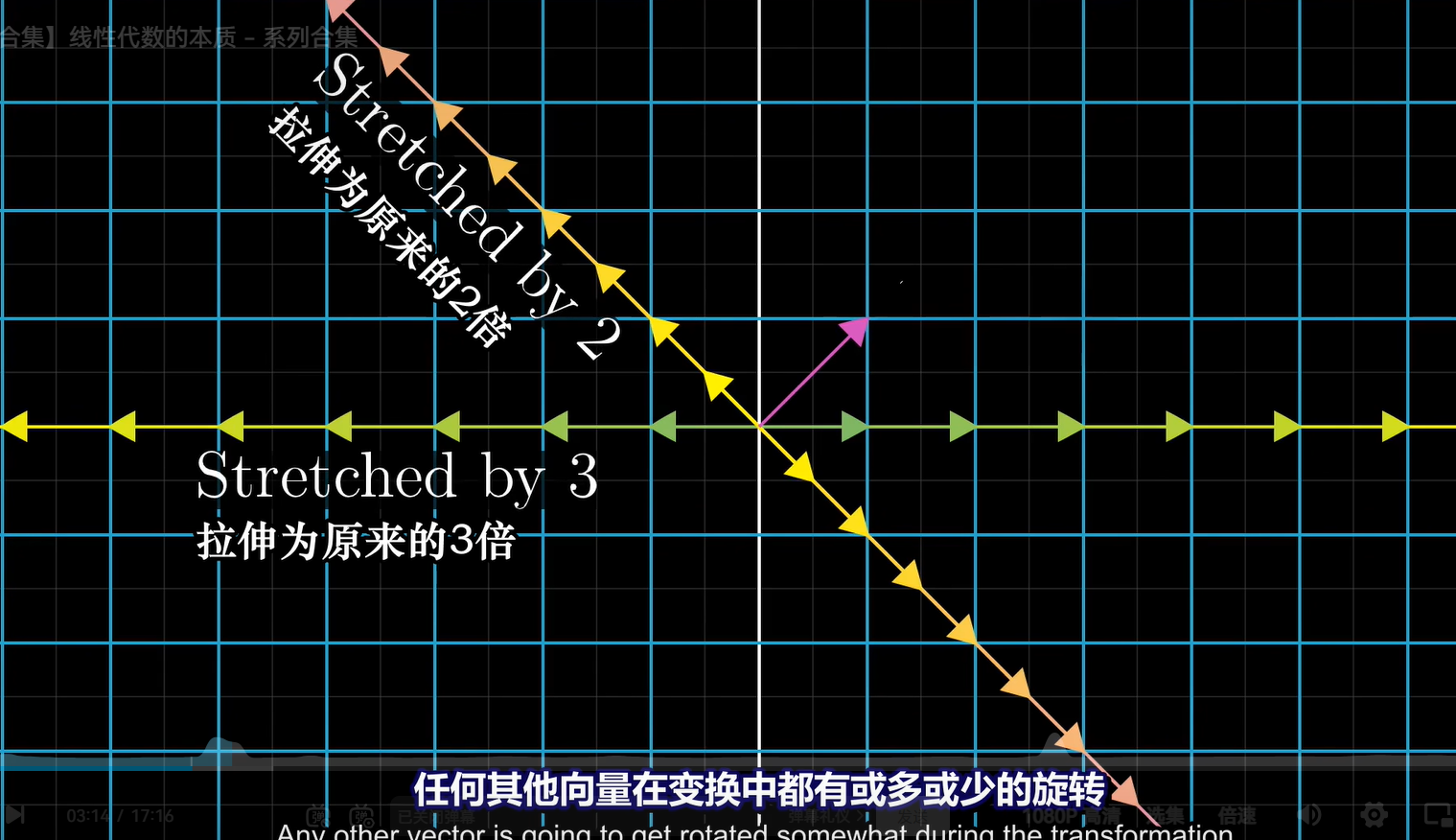
在这个变换中基本上所有的向量都偏移了其原来张成的空间的位置,但某些特殊向量的确留在它们张成的空间里,这意味着这个矩阵变换对它的作用仅仅是拉伸或者压缩而已
对于该变换来讲,有 (1,0)向量所在直线与 (-1,-1)所在直线(注意是直线,怪不得之前求特征向量的时候总会带上k)仅仅被拉伸或压缩,没有被旋转
这俩就是特征向量,每个特征向量都有一个所属的值,被称为“特征值”,即衡量特征向量在变换中拉伸或压缩比例的因子(这也是特征值的乘积等于行列式的原因,缩放倍数)
使用价值
考虑一个三维空间中的旋转,如果你能找到这个旋转的特征向量,那么你找到的就是旋转轴! 而且把一个三维旋转看成绕某个轴旋转一定角度,要比考虑相应的3×3矩阵直观得多
比如旋转矩阵:
求解特征向量/特征值的方法
用A对特征向量v进行线性变化,特征向量v只会回被拉伸或者缩短,所以用Av=λ v
转化一下:
我们现在需要找到合适的λ,使A-λ这个矩阵的张成空间收缩,也就是行列式的秩变少,这也是为什么我们在计算的时候常常使用行列式的值来计算,实际上用行变换的线性变换也可以
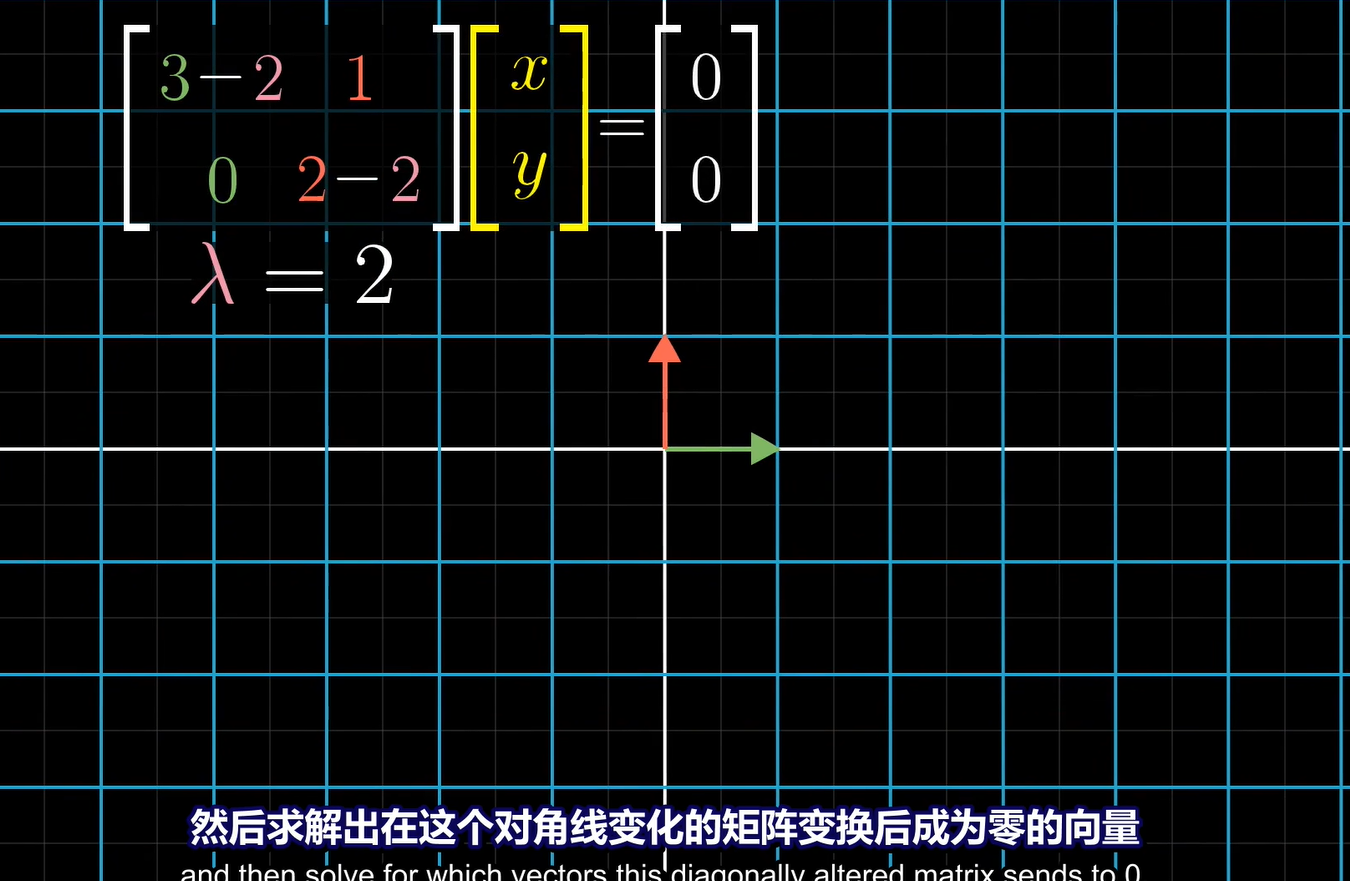
求特征向量:
需要注意的是二维线性变换不一定有特征向量
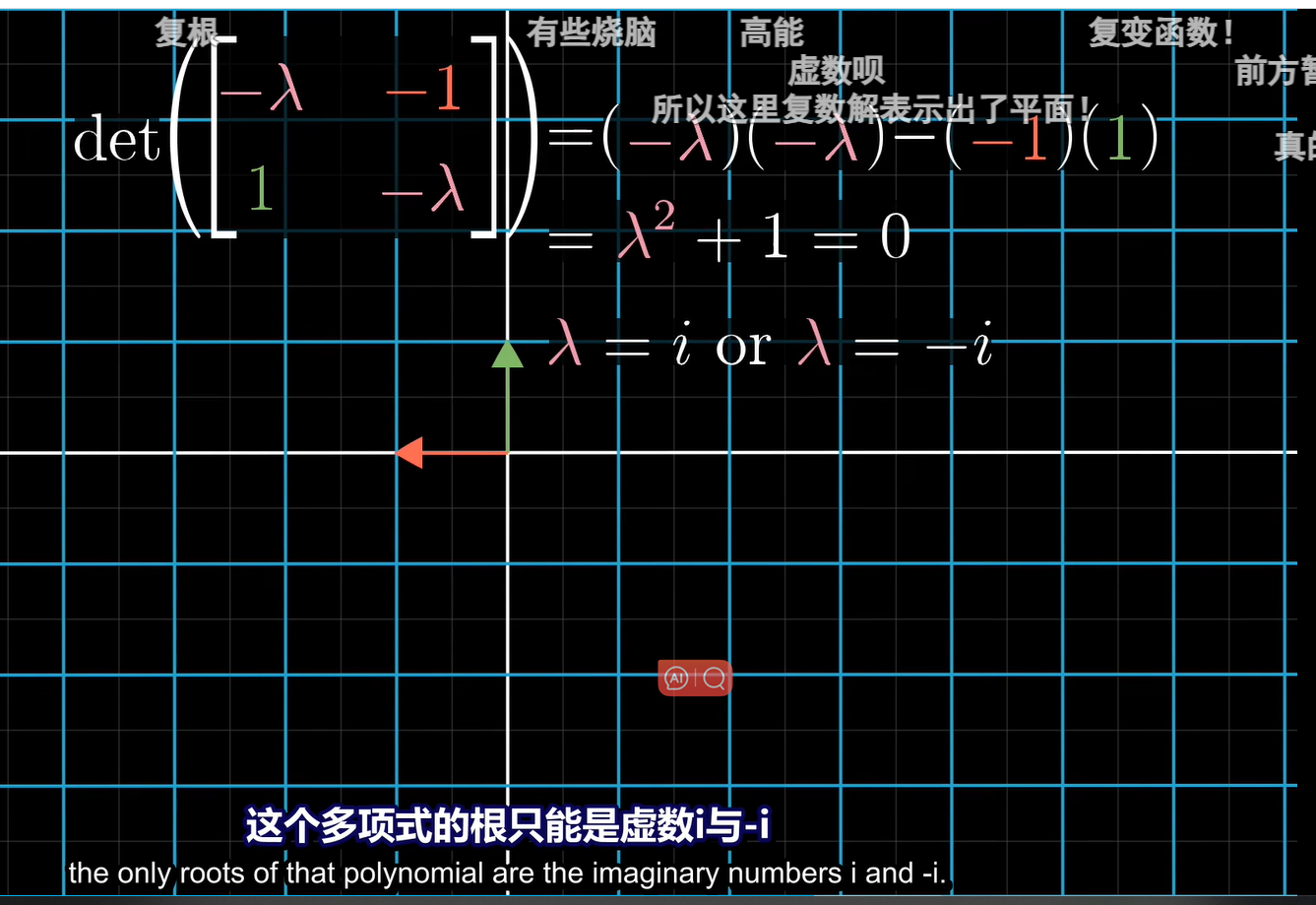
比如90°旋转,其张成的空间中的向量都在变换,故没有特征值与特征向量
:
没有实数解表示没有特征向量
特征基 (相似对角化)
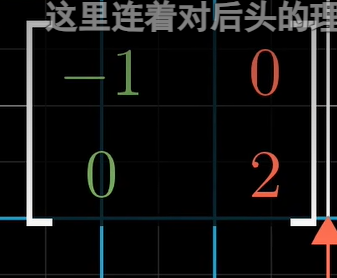
我们的基向量恰好是特征向量:
x轴变为-1倍,y变为2倍
这种矩阵是对角矩阵,其性质在计算过程非常好用
但,遗憾的是,我们大多数的矩阵变换的基向量都不是特征向量,不过我们可以变换我们的坐标系使这些特征向量为基向量,即用特征向量做基 ,使基变换后的坐标系相对于矩阵变换是对角的矩阵变换(因为特征向量它所处的坐标系的基向量在变换中只进行了缩放,故以特征向量做基可变换为对焦矩阵!!!)
这就涉及当上节的基变换了!!!
假设 A是我们的变换矩阵,P是变换矩阵的特征向量组成的矩阵,我们变A所属的左边系为以P矩阵为基的左边系,即:
,其中λ为特征值
注意,前提是特征向量够组成一个矩阵
九、抽象向量空间
1、线性运算
即满足一下条件的L()
L(A+B) = L(A)+L(B)
L(kA)=kL(A)
2、函数求导是线性变换
那我们可以把多项式求导转化成矩阵求导
十、用几何的角度理解克莱姆法则
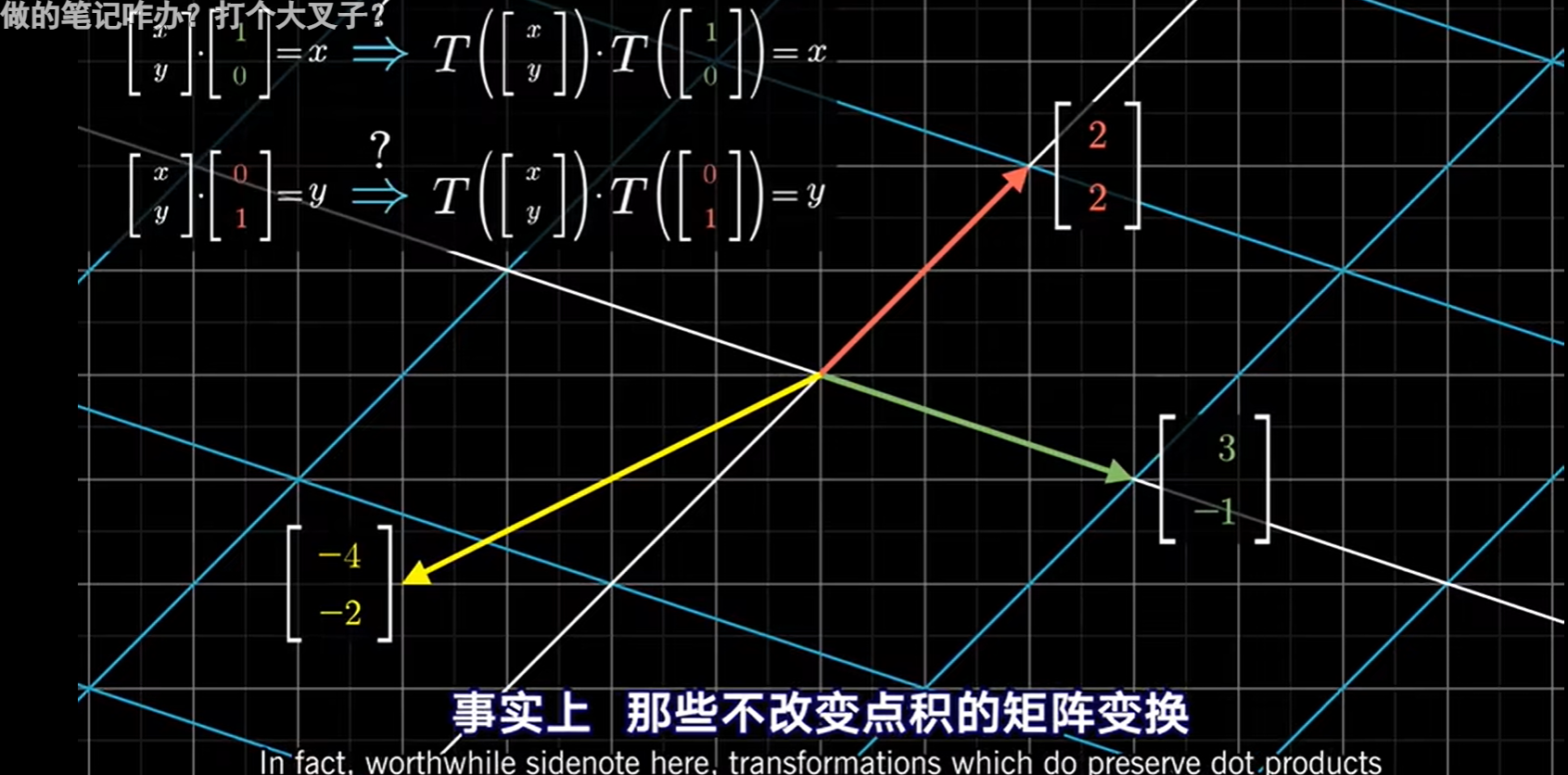
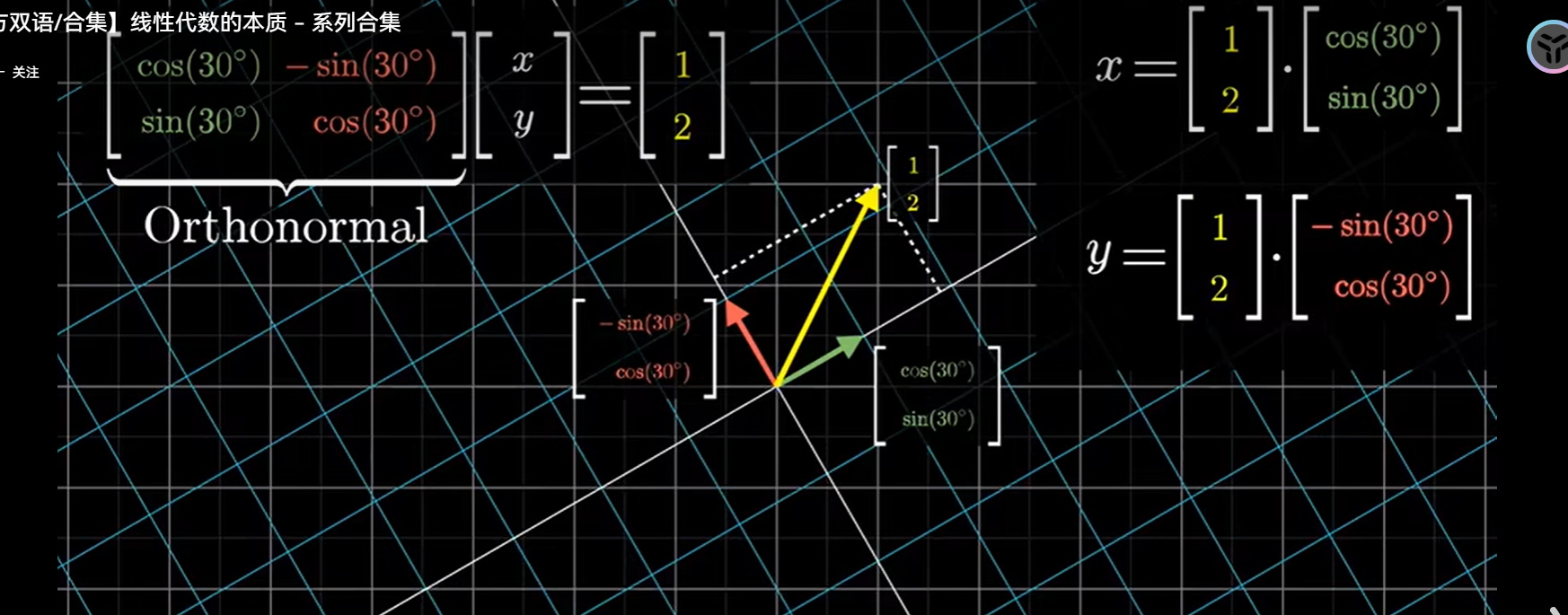
前置知识---正交变换
它们使基向量在变换后依然保持单位长度且相互垂直,可以想象成旋转矩阵,相当于作刚体运动没有拉伸压缩或变形
变换后的两向量相乘 == 变化前的俩向量相乘 => 正交变换
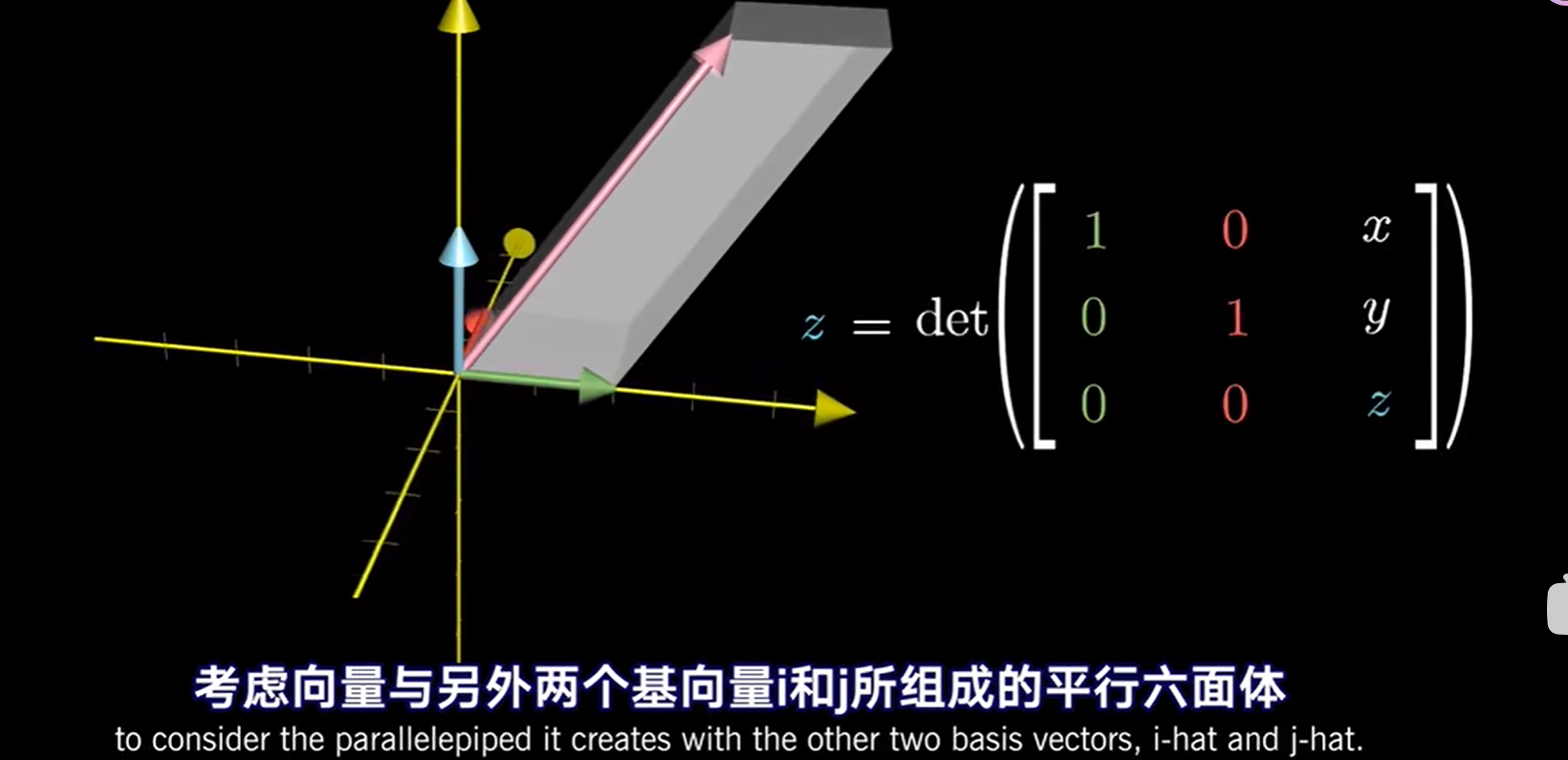
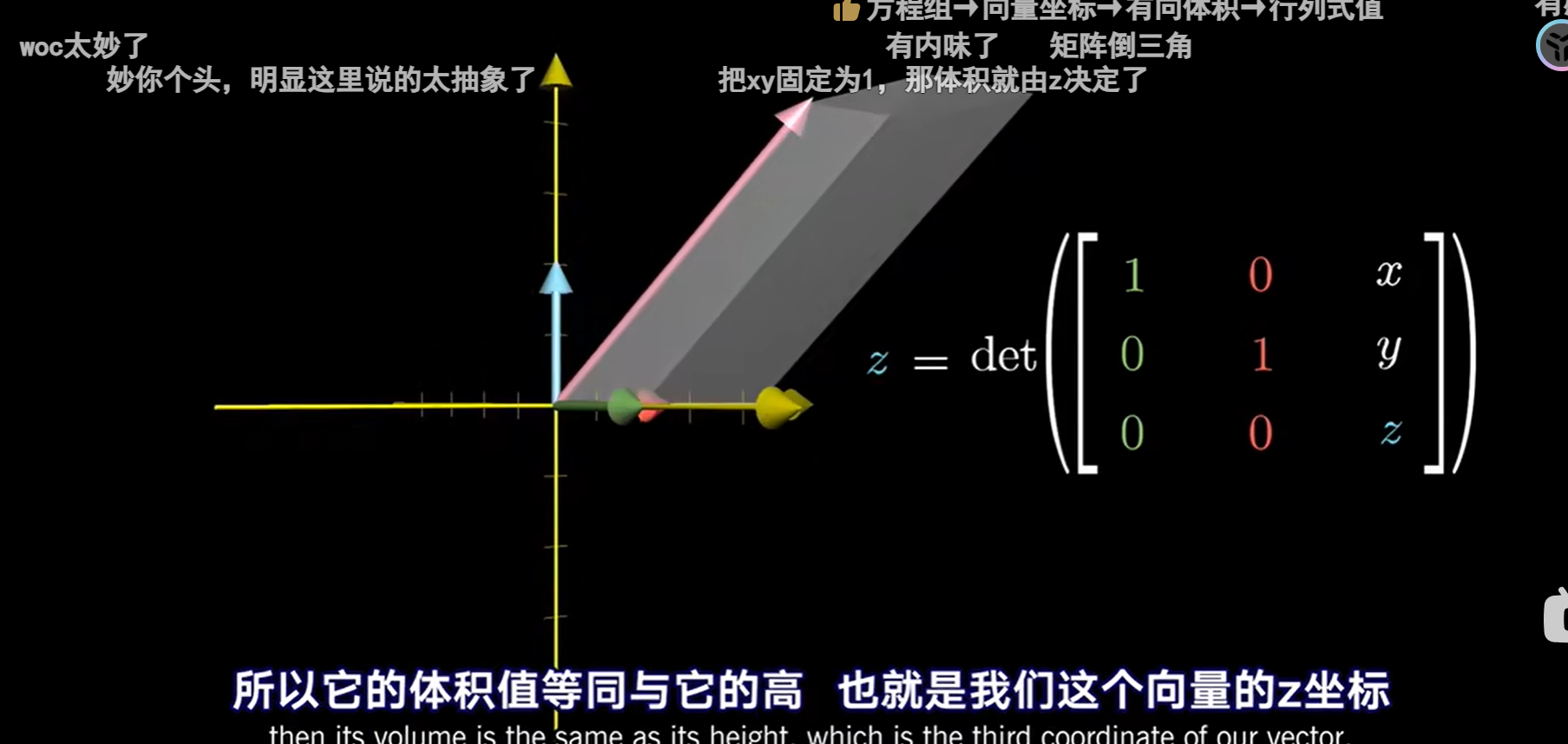
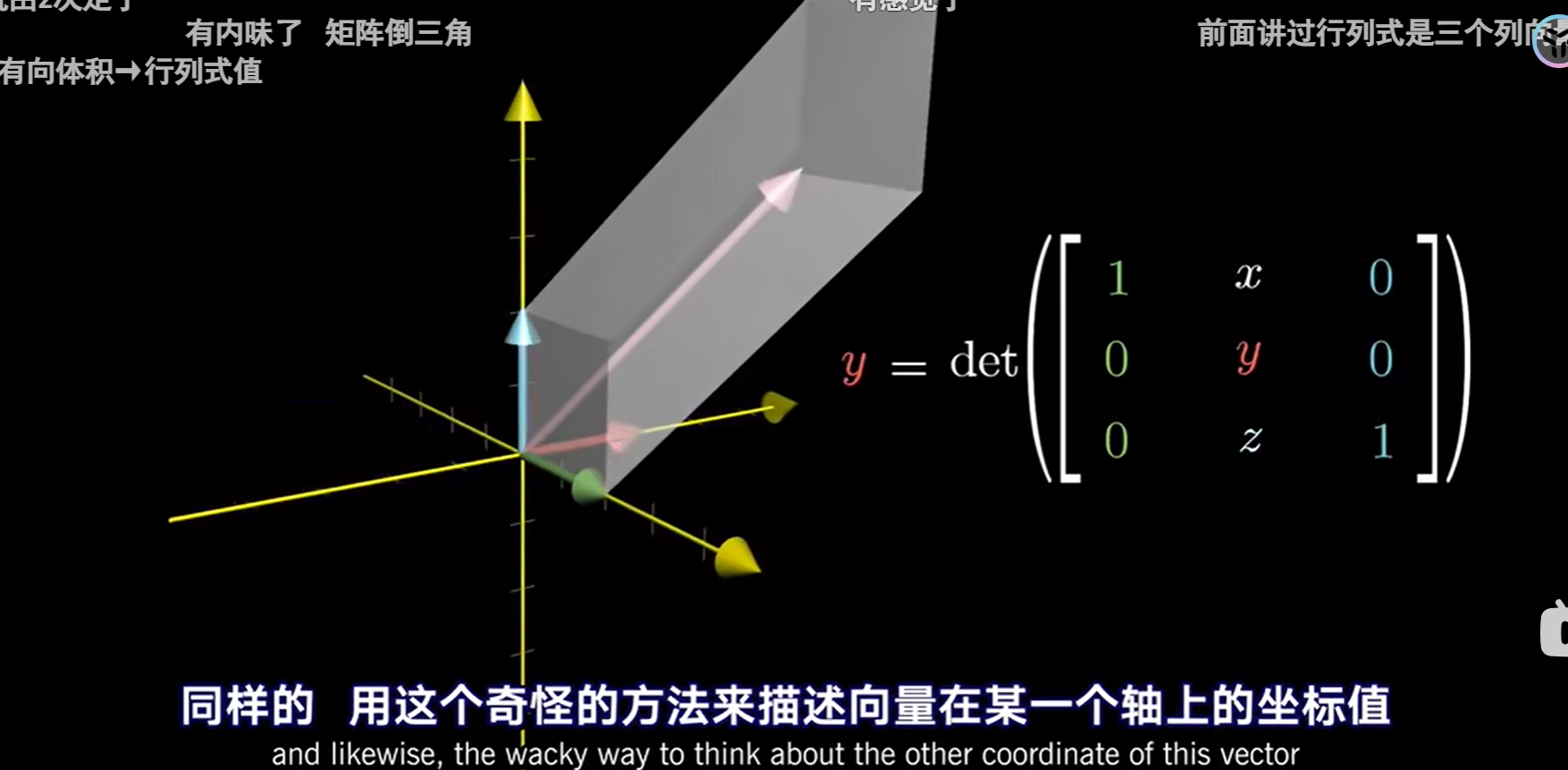
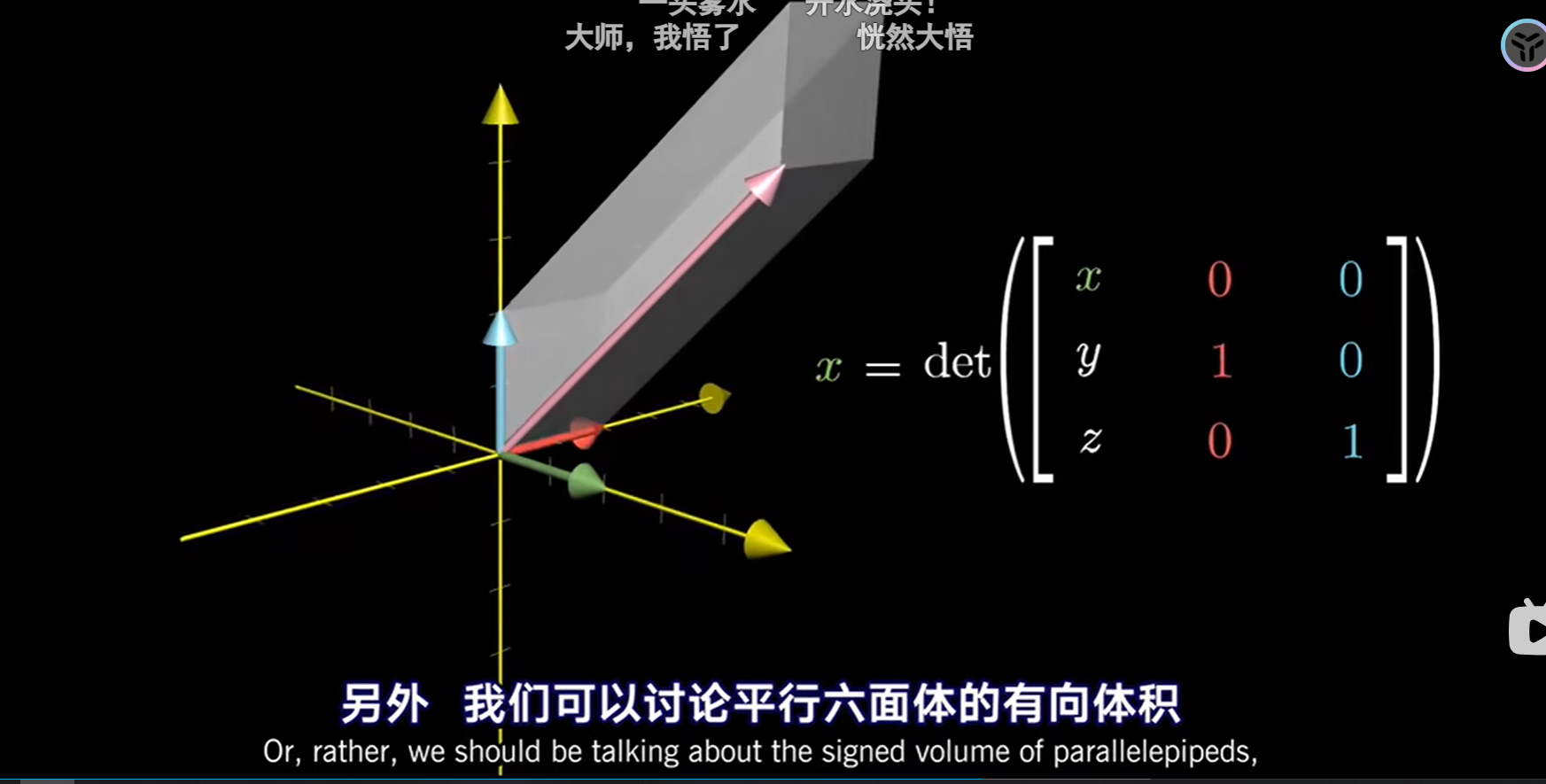
前置知识---使用行列式表示向量坐标
上面这一部分告诉了我们,输入向量(x,y,z)与基坐标i,j组成的平行六面体体积就是z
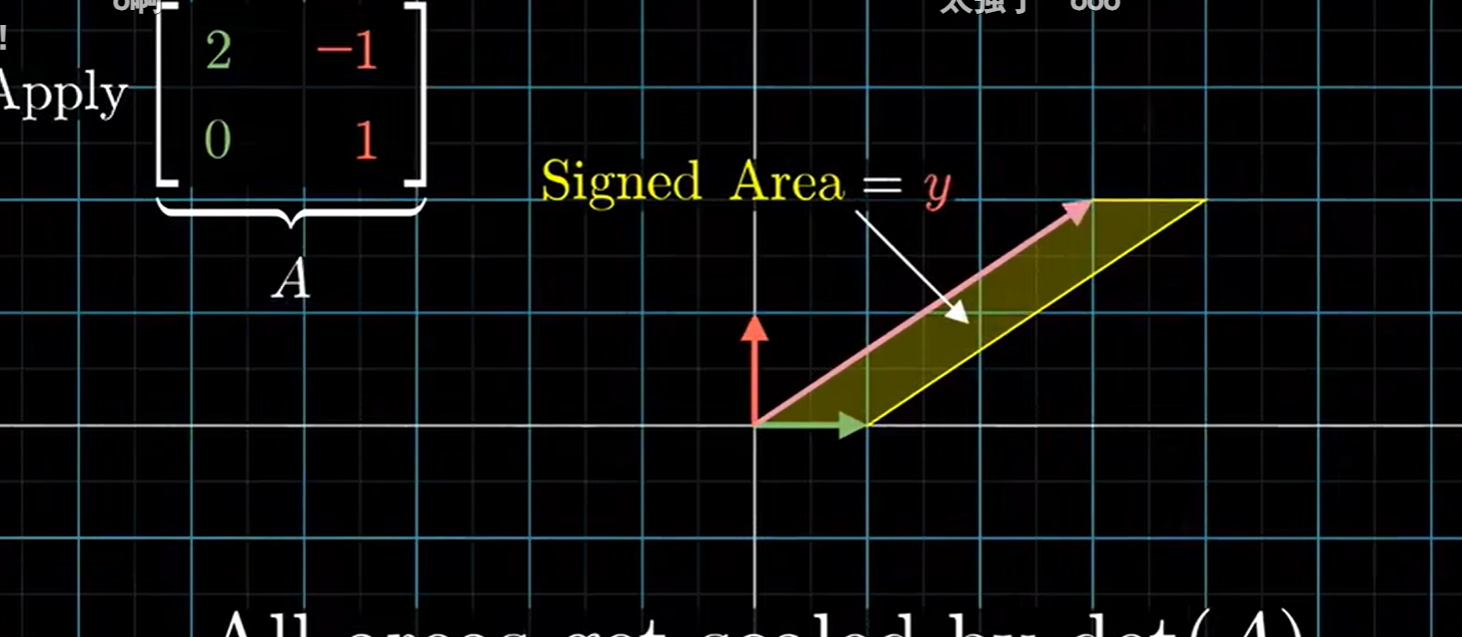
同理对于二维,输入向量(x,y)与基向量i所组成的平行四面体,其有向面积就是输入向量的y坐标
克莱姆法则
那么我们进行线性变换 后区域面积值的伸缩比例等于给定矩阵的行列式值。原来基向量i和,[x,y]围成的面积是y,现在变成了Area=det(A)y
因此就有:
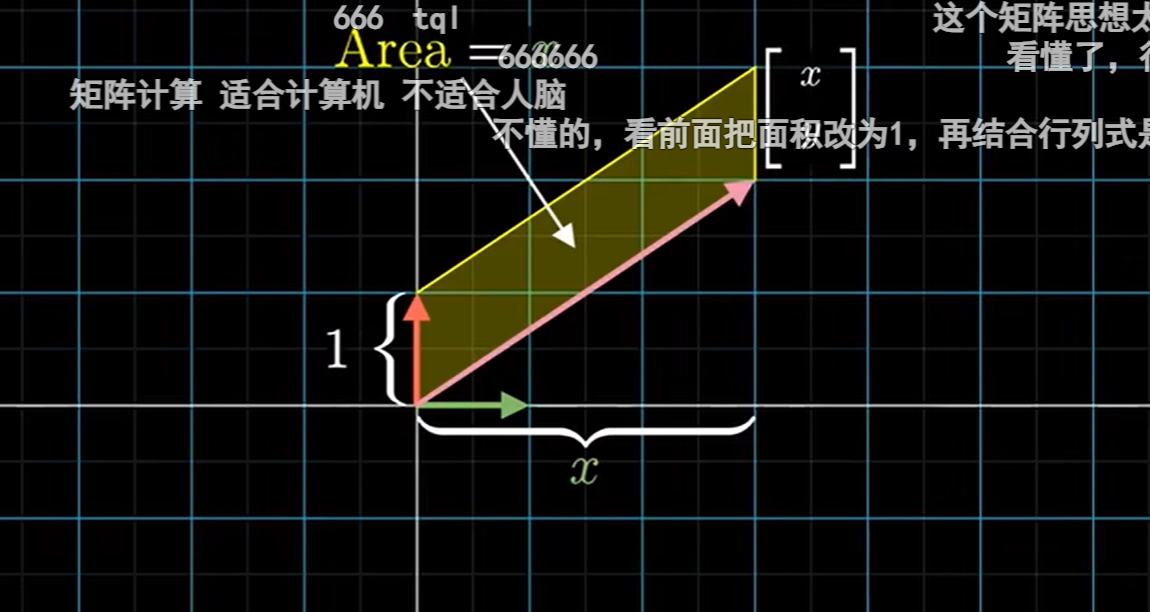
至于分子Area为什么这么构造,是因为我们之前的图形是这样的:
是(x,y)关于i基的平行四边形,其底的大小为单位1(若是关于j基的,高就为单位1)!
变换之后是这样的:
显而易见 经过 的变换后,原平行四边形的底从 i基变成了
那么求Area这个平行四边形的面积就是 辣
求x也是同理:
总结
- 求y的话,以i为基,y为研究对象
- 构造[x,y]与i基组成的平行四边形的面积与经过矩阵A变换后的平行四边形面积,[x,y]与i基组成的平行四边形的面积就等于变换后的平行四边形面积比上变换矩阵A的平行四边形面积
- 使用 y 表示以i为基底的平行四边形面积
- 又A变换后的平行四边形面积可求,并且矩阵A是给出的,其平行四边形面积也可求,故可以求出y
- -------------------上面是求y,下面求x-------------------
- 略
十一、以几何的角度理解二次型の我的见解
参考: https://www.matongxue.com/madocs/228/
二次型主要解决多元二次函数的问题
前提知识
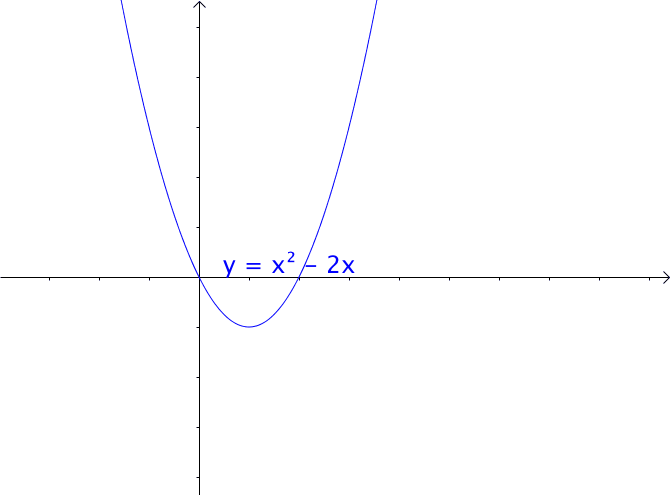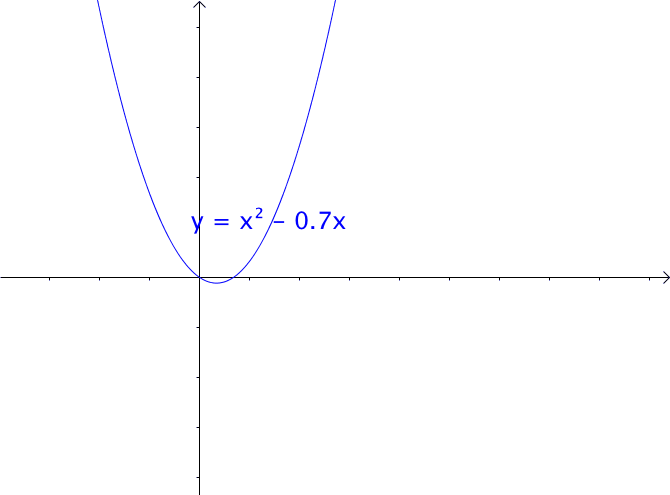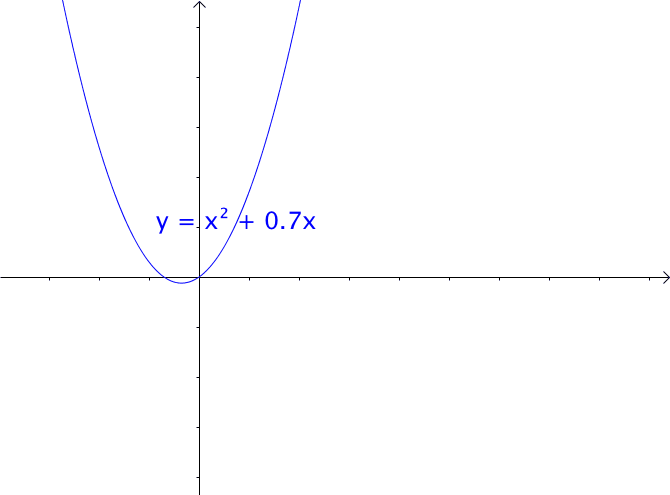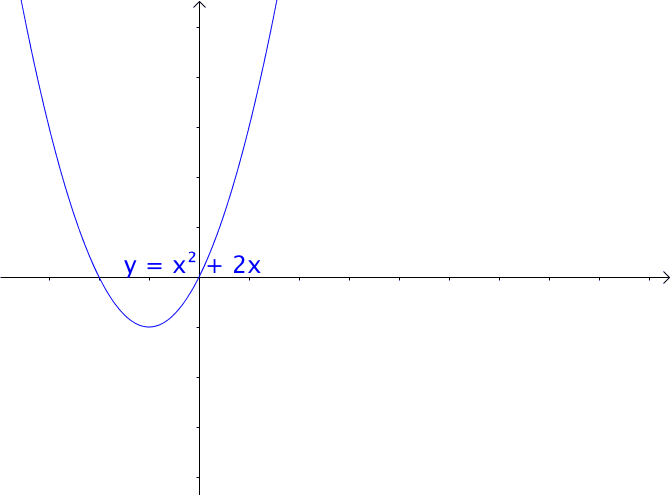
1、对于一元二次函数,我们只改变一次项与常数项是不会改变函数的图像的
2、对于二元二次函数也是这样:
他们的形状没有改变,那么代表这个图形的各种属性都没有改变(如面积,周长之类的)
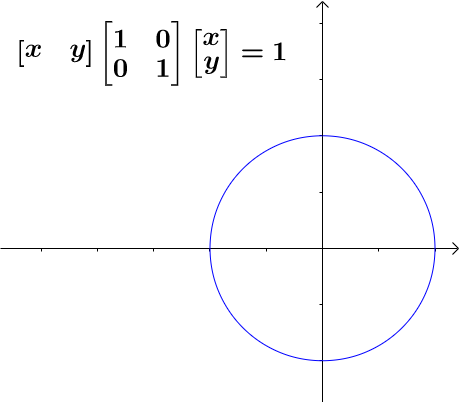
3、圆的二次型
一个单位圆的二次型表示是这样的:
它以x,y轴作为基
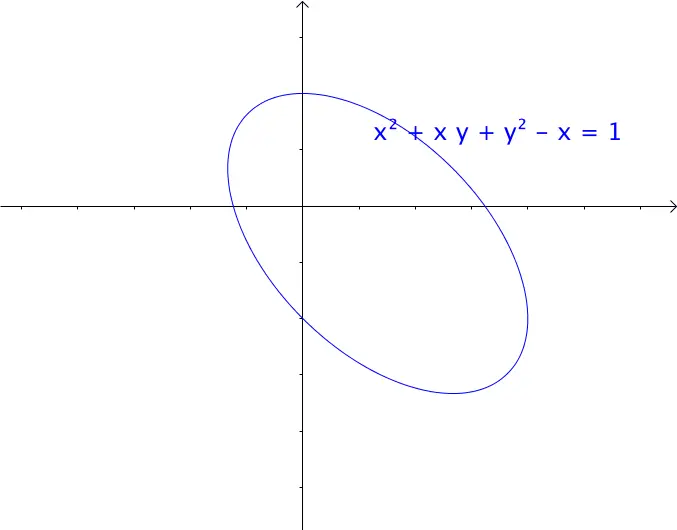
4、椭圆的二次型
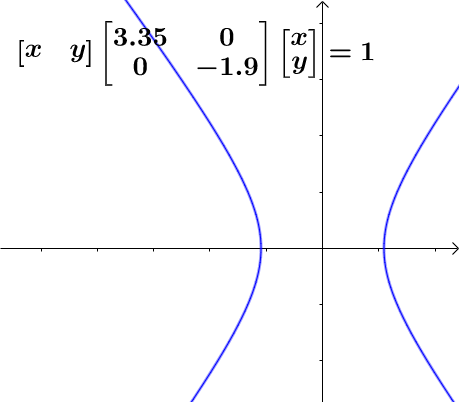
5、双曲线的二次型
可以发现,圆、椭圆、双曲线都是线性相关的
二次型对于几何图形的改变
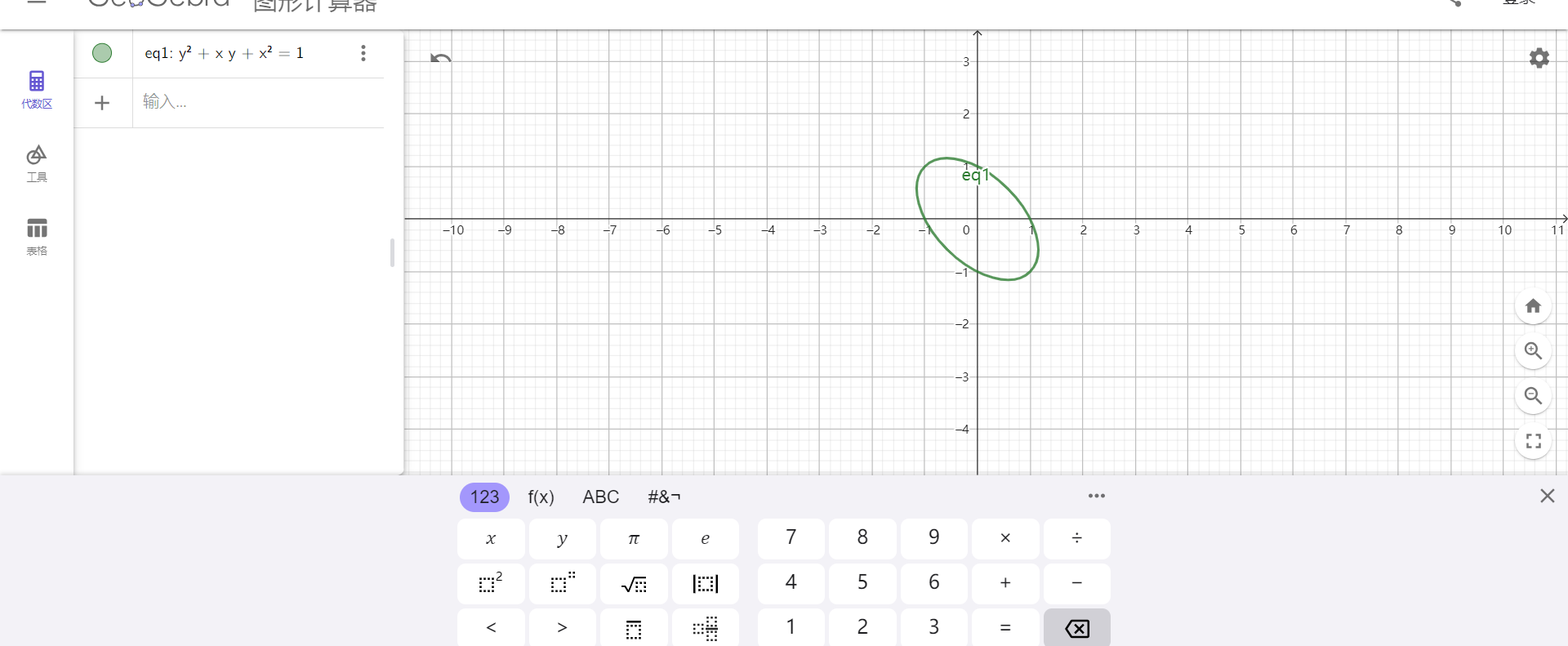
我们有这样歪着的椭圆:
图中表示的是该椭圆以 x,y为基的图形
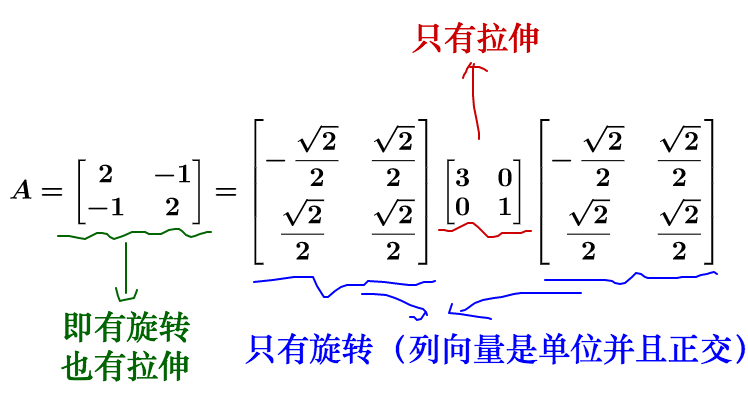
我们把其正交分解
可以得到上图这个图形,上面这个图形是以作为y基的图形
并且,由于是Q是正交的,故以Q中的向量做基,只会旋转坐标轴,不会压缩坐标轴,故与A的唯一区别就是坐标轴被旋转了 几度
我们完全可以把对于A的研究转化成对于的研究,以此大大简化研究难度
比如我们完全可以把
转化为 来处理:
=>
的特征值是: 1.5、0.5;特征向量是: [0.707,0.707],[0.707,-0.707]
正定
正定的定义
正定、半正定、负定的例子
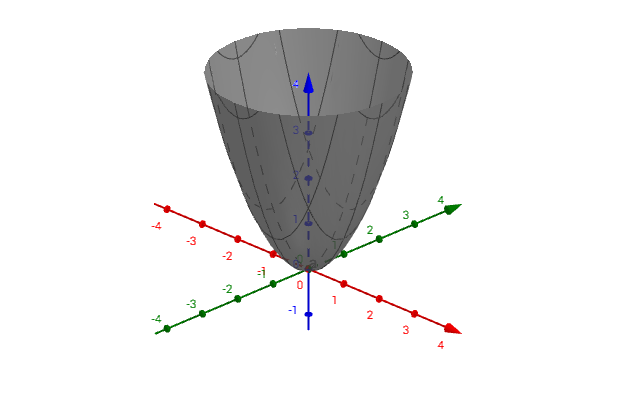
正定
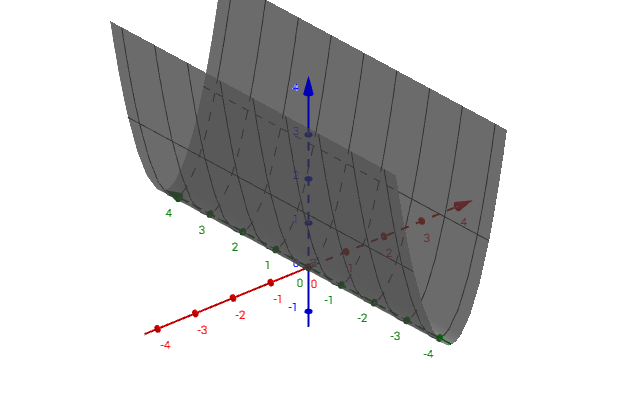
半正定
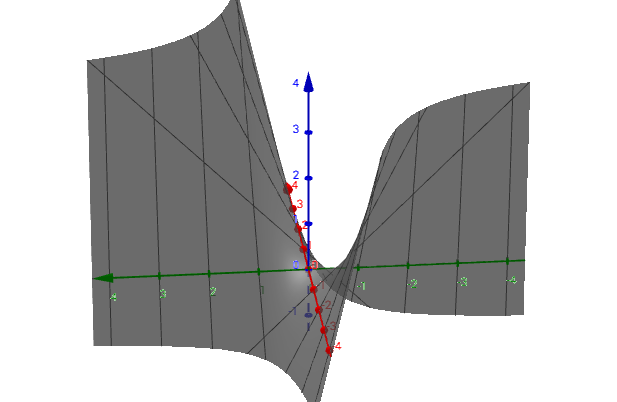
不定:
十二、其他的一些补充(持续补充...
1、以几何的角度理解 AB=BA,且A有n个互不相等的特征值,则A的特征向量都是B的特征向量
非几何角度的证明过程:
几何角度的理解:
首先从 开始
我们设A = ,B = ,
有A*B * s如下
而如果我们采用 B * A * s:
可以发现得到的向量结果大不相同,其本质原因是我们的基底变的不一样了,前者的基底分别是(-1,0)、(1,1);而后者的基底是(-1,1)、(0,1)。
如果A*B或B*A前后变化的基底一样的话,对向量s的变化结果是肯定一样的,这就引出了 "则A的特征向量都是B的特征向量" (因为在相似变换的时候特征向量就是基底)
__EOF__

本文链接:https://www.cnblogs.com/lordtianqiyi/p/17791138.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!




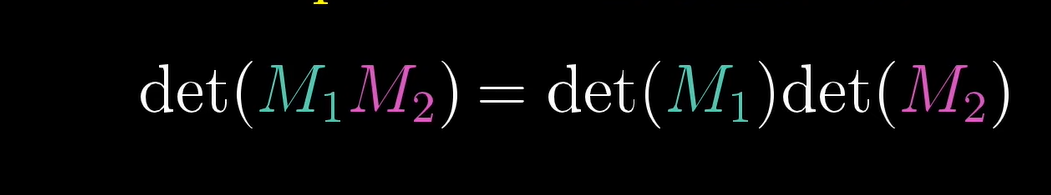










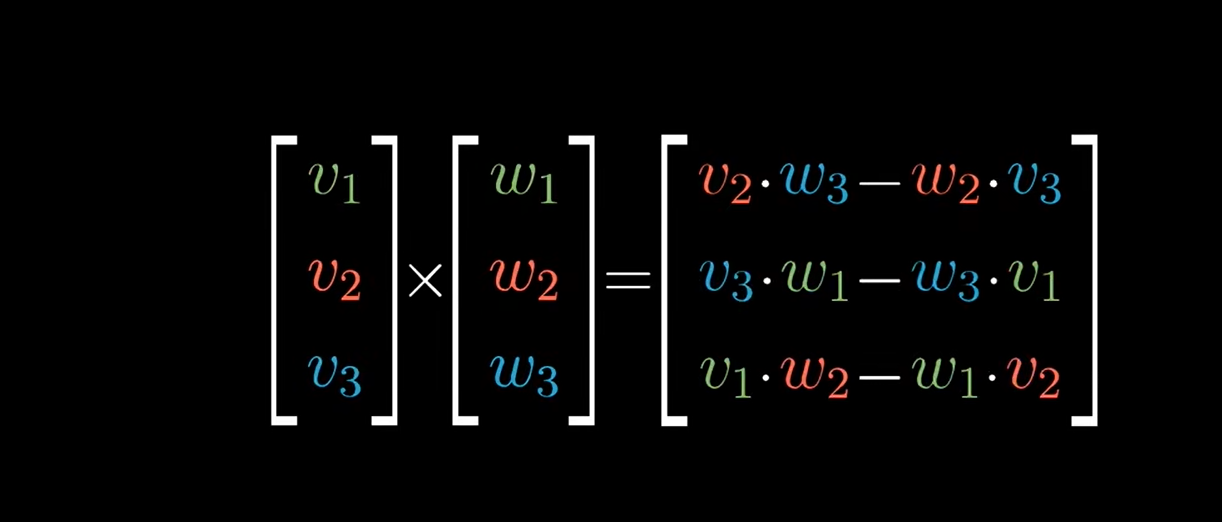

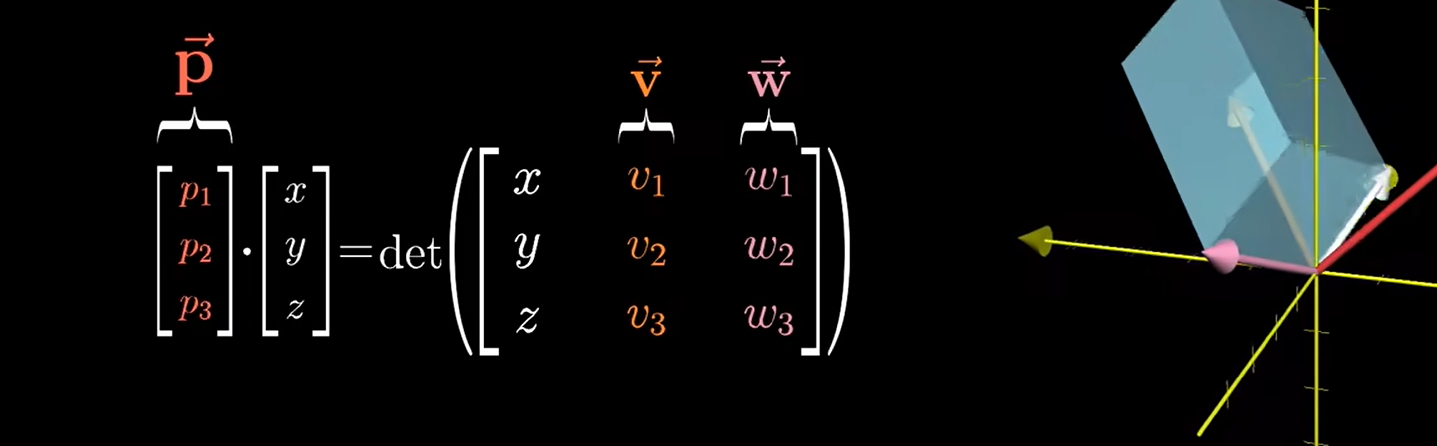



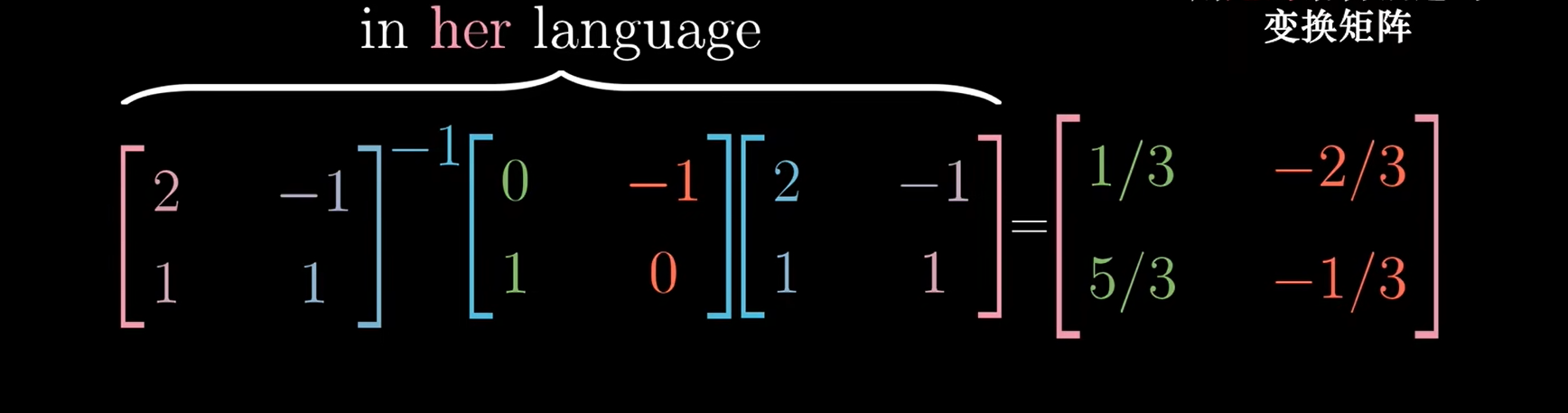
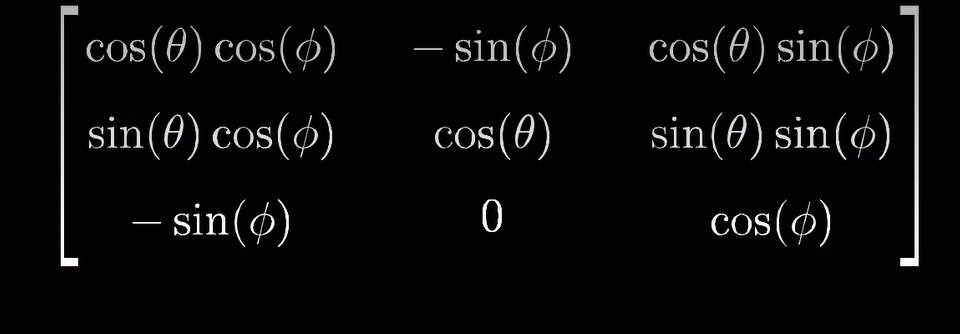

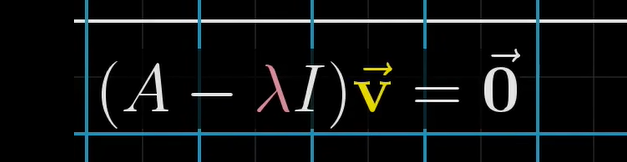





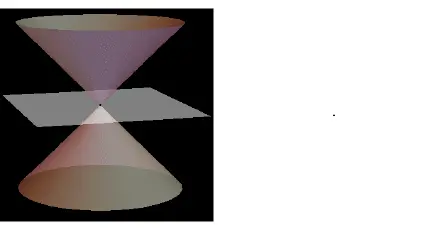
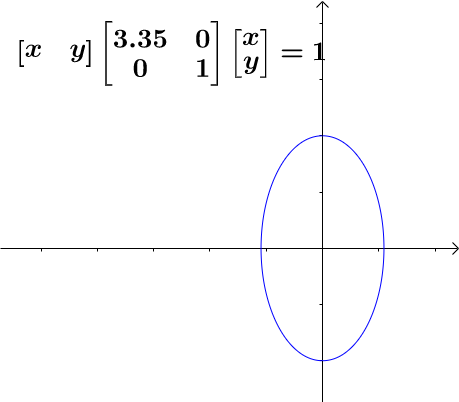
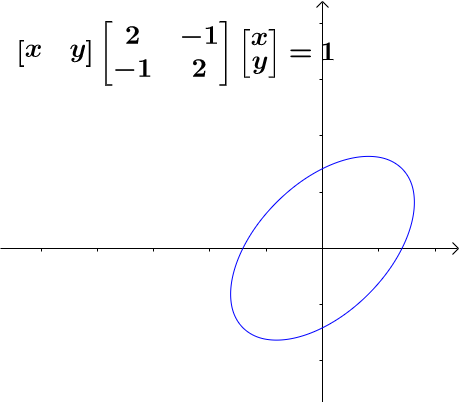






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署