王道408---DS---图
图有关的概念
1、连通图、连通分量是相对于无向图说的,而强连通图、强连通分量是相对于有向图说的
2、生成树,连通图的生成树是包含图中全部顶点的一个极小连通子图。若砍去一条边,则一定变得非连通
3、极大连通子图与极小连通子图,极小连通子图就是生成树,极大连通子图就是无向图的连通分量
极大要求包含该连通子图的所有边,极小要求保持连通且边最小
连通图的连通分量/极大连通子图就是它自己
4、简单路径、简单回路:
在路径序列中,顶点不重复出现的路径称为简单路径。
除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
图的存储
一般有四种方法---邻接矩阵法、邻接表法、十字链表法、邻接多重表,常用的只有前两种
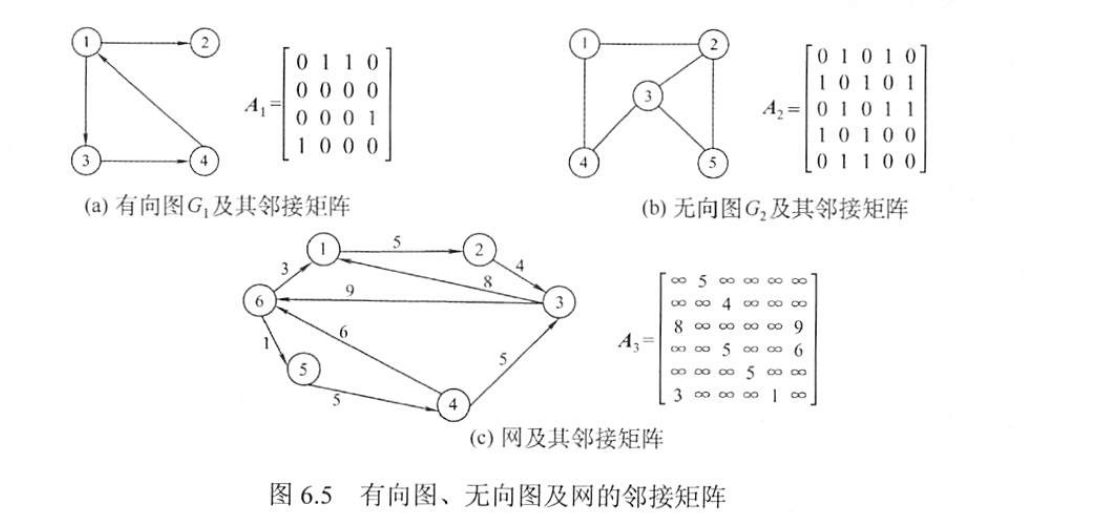
邻接矩阵法
需要注意的是
1、无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储。
2、稠密图适合使用邻接矩阵的存储表示。
3、
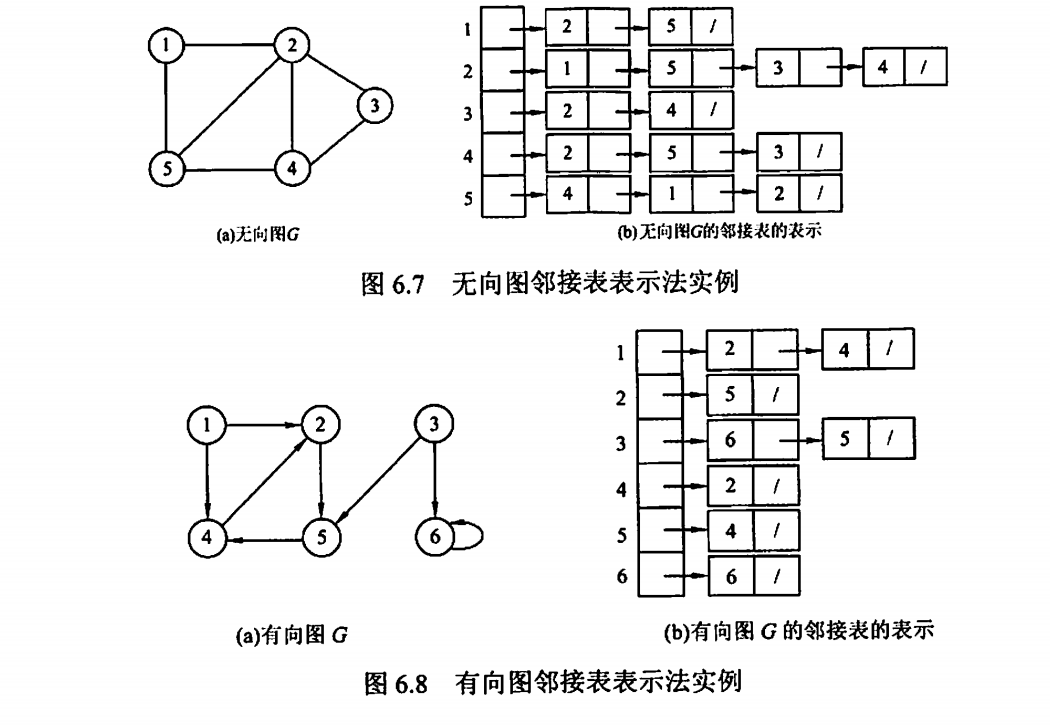
邻接表法
对于稀疏图,采用邻接表存储比较好
求度的时候需要遍历整个邻接表,为此引出了十字链表法:
十字链表法
十字链表法用于有向图
之前写过一篇:
https://www.cnblogs.com/lordtianqiyi/p/17739953.html
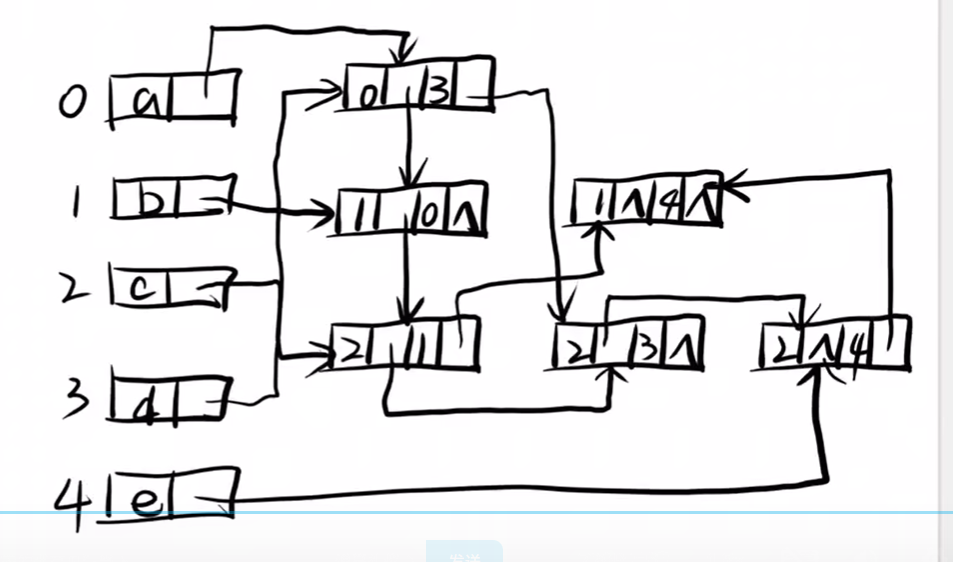
邻接多重表
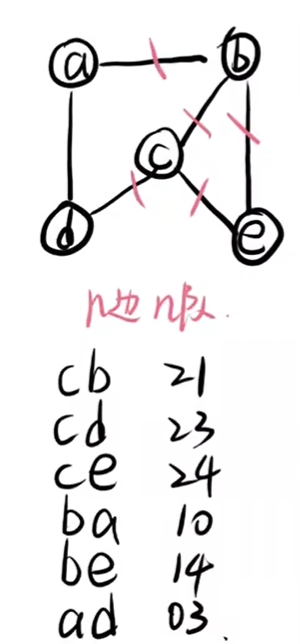
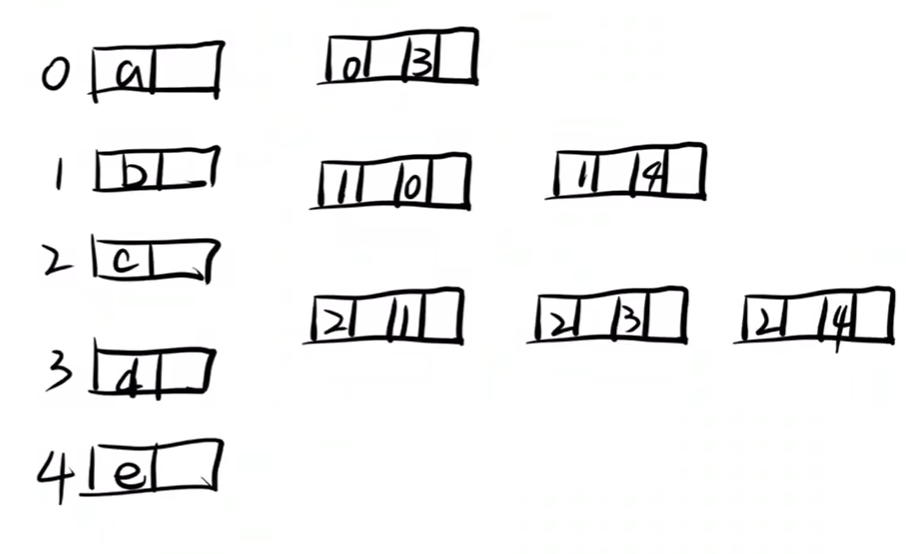
邻接多重表的画法
比我想象中的简单
1、写出所有的边的关系
2、先画出顶点以及边
3、链接
边的第二个数据项ilink代表指向下一条依附于顶点ivex的边
第四个数据项jlink指向下一个依附于顶点jvex的边
图的遍历
BFS
类似于二叉树的层序遍历
Dijkstra、prim算法就使用到了广度优先的思想
空间复杂度: O(V)
时间复杂度: O(V+E) // 邻接表法 或 O(V^2) // 邻接矩阵法
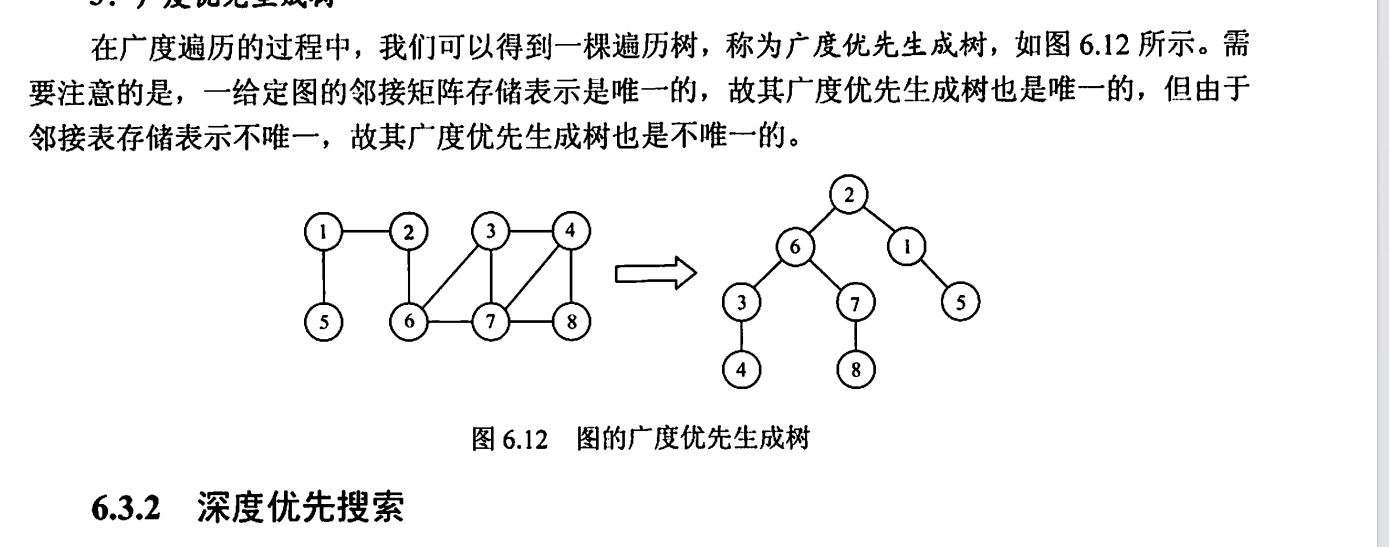
BFS---广度优先生成树
DFS
类型于二叉树的先序遍历
需要一个递归的栈,空间复杂度为O(V)
邻阶矩阵的时间复杂度是O(V^2)
邻阶表的时间复杂度是O(V+E)
深度优先遍历还可以判断是否存在回路
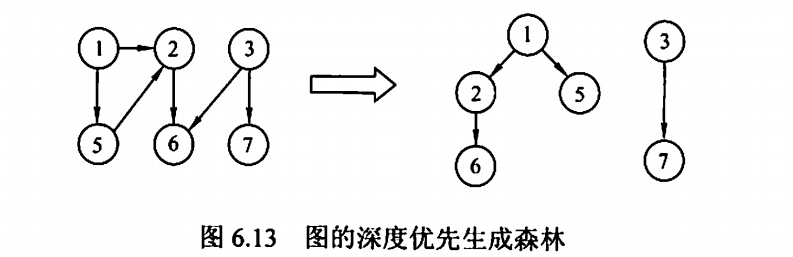
DFS---深度优先生成树
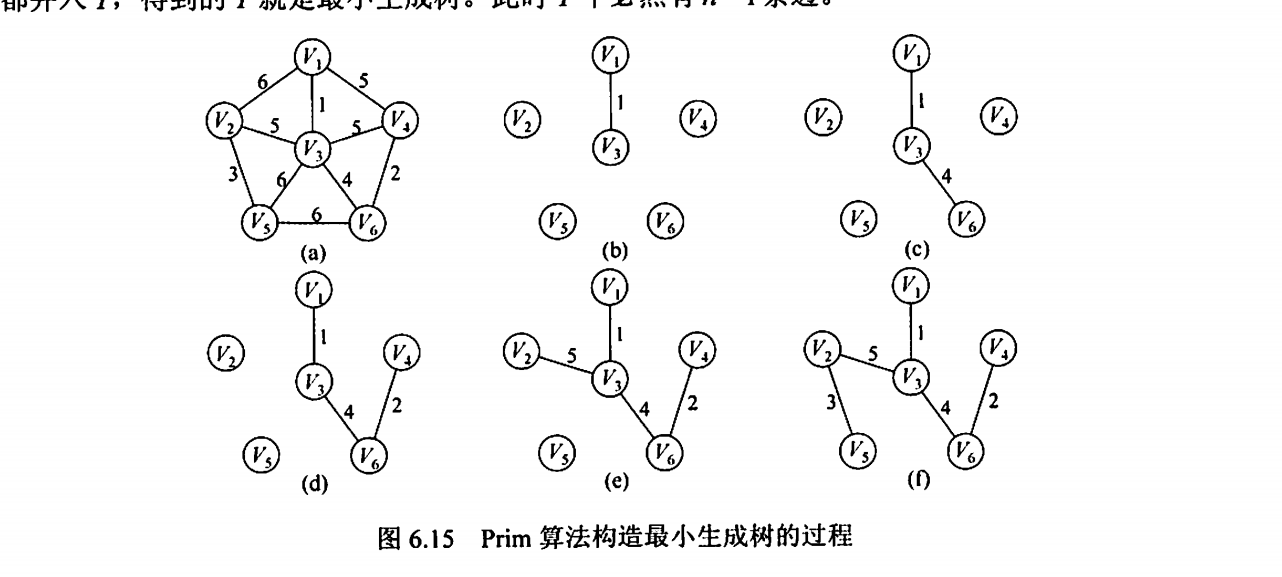
Prim算法
MST,最小生成树
类似于Dijkstra算法
适合求稠密图的MST
时间复杂度: O(V^2)
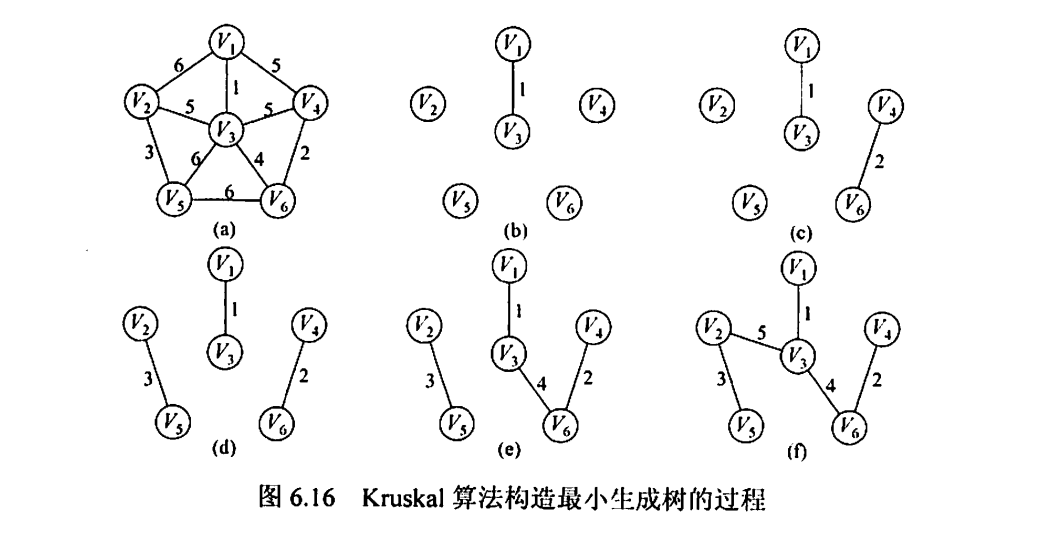
Kruskal算法
时间复杂度:O(ElogE)
适合求边稀疏顶点多的图的MST
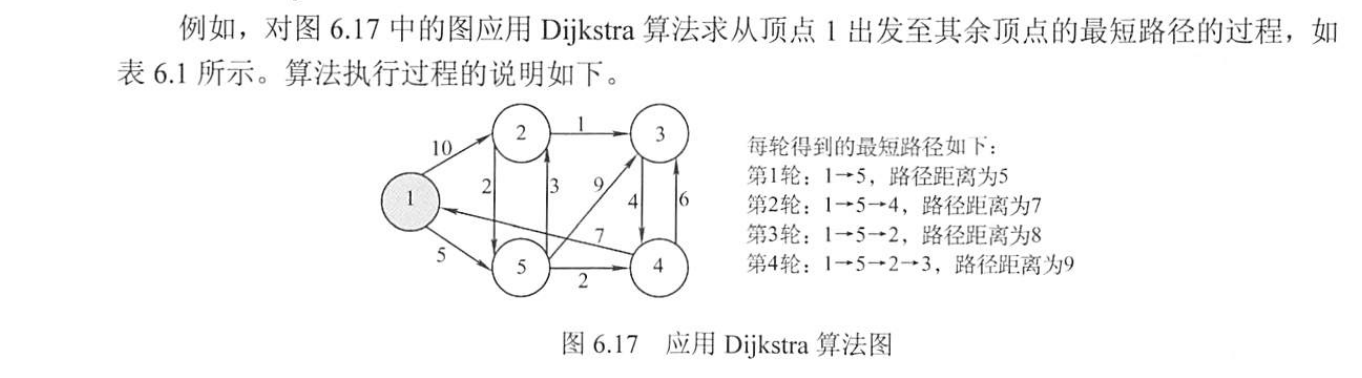
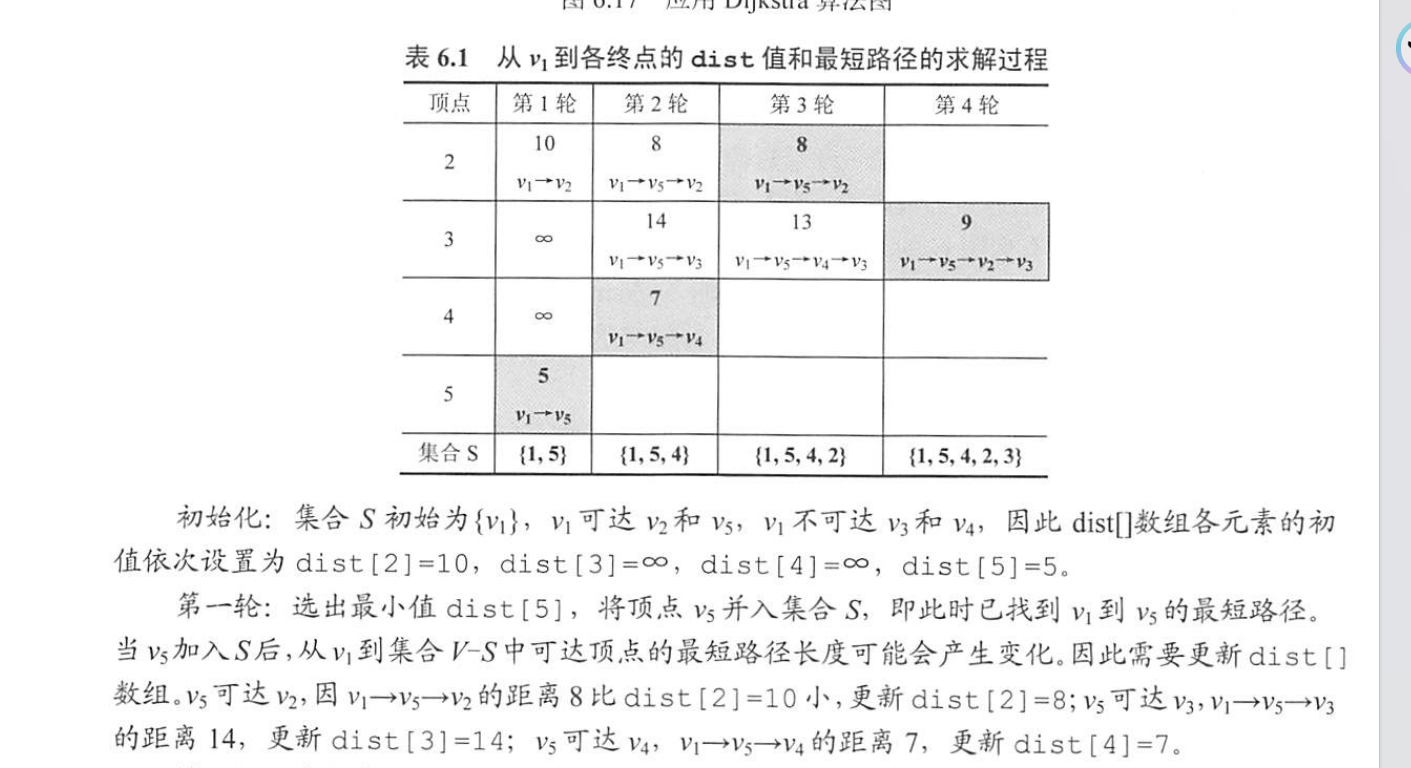
Dijkstra算法求单源最短路径
不适用于负权值
时间复杂度为O(V^2)
Dijkstra 算法思路
Dijkstra算法求的是单源最短路径,我们假设这个单源是点A,即要求点A到其他结点的最短距离
0、设置一个st数组,记录已经是最短路径的顶点。设置dist数组,存储目前已经探明的点A到其他结点的距离。设置g数组,用来记录初始下各个点之间的距离
1、第一重循环下,每一轮的任务: 首先循环遍历dist数组,从所有尚未找到最短路径的中找到目前距离A最近的结点,记为x,将其加入最短路径st中,随后以x为枢轴,A为一边,所有的非最短路径结点为另一边,循环遍历并更新dist距离( dist[j] =min(dist[j],dist[t]+g[t][j]); )
2、循环即可
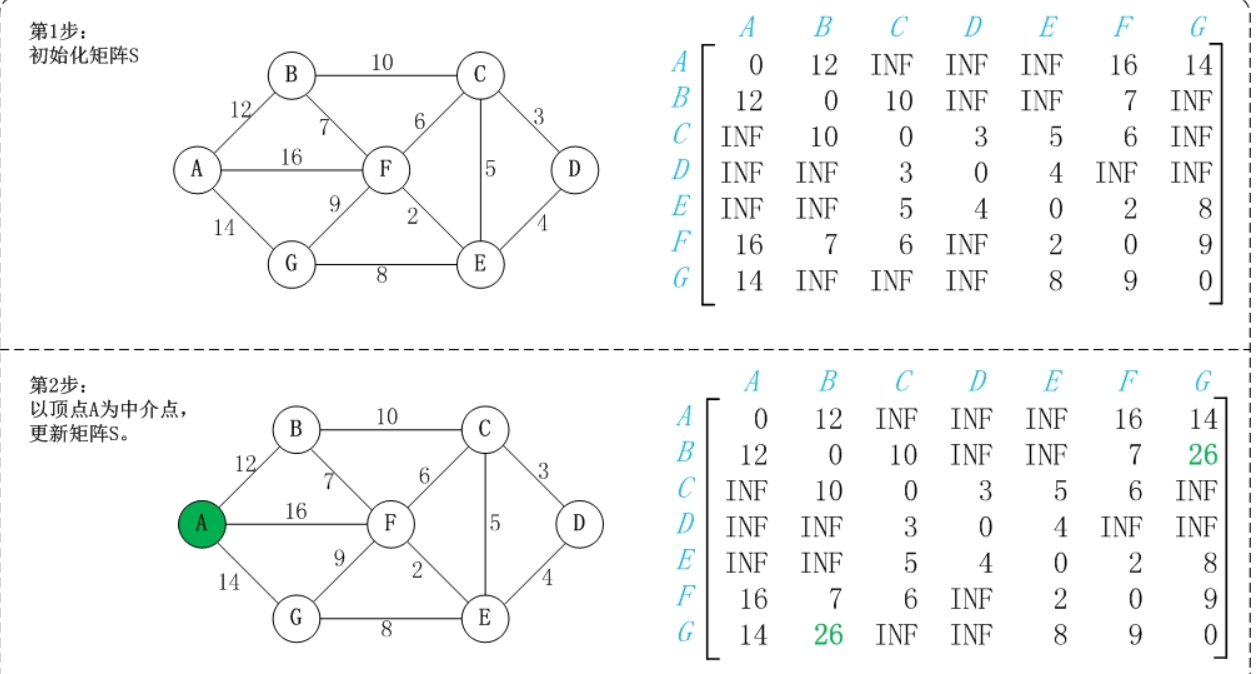
Floyd算法求多源最短路径
时间复杂度为O(V^3)
算法思想:
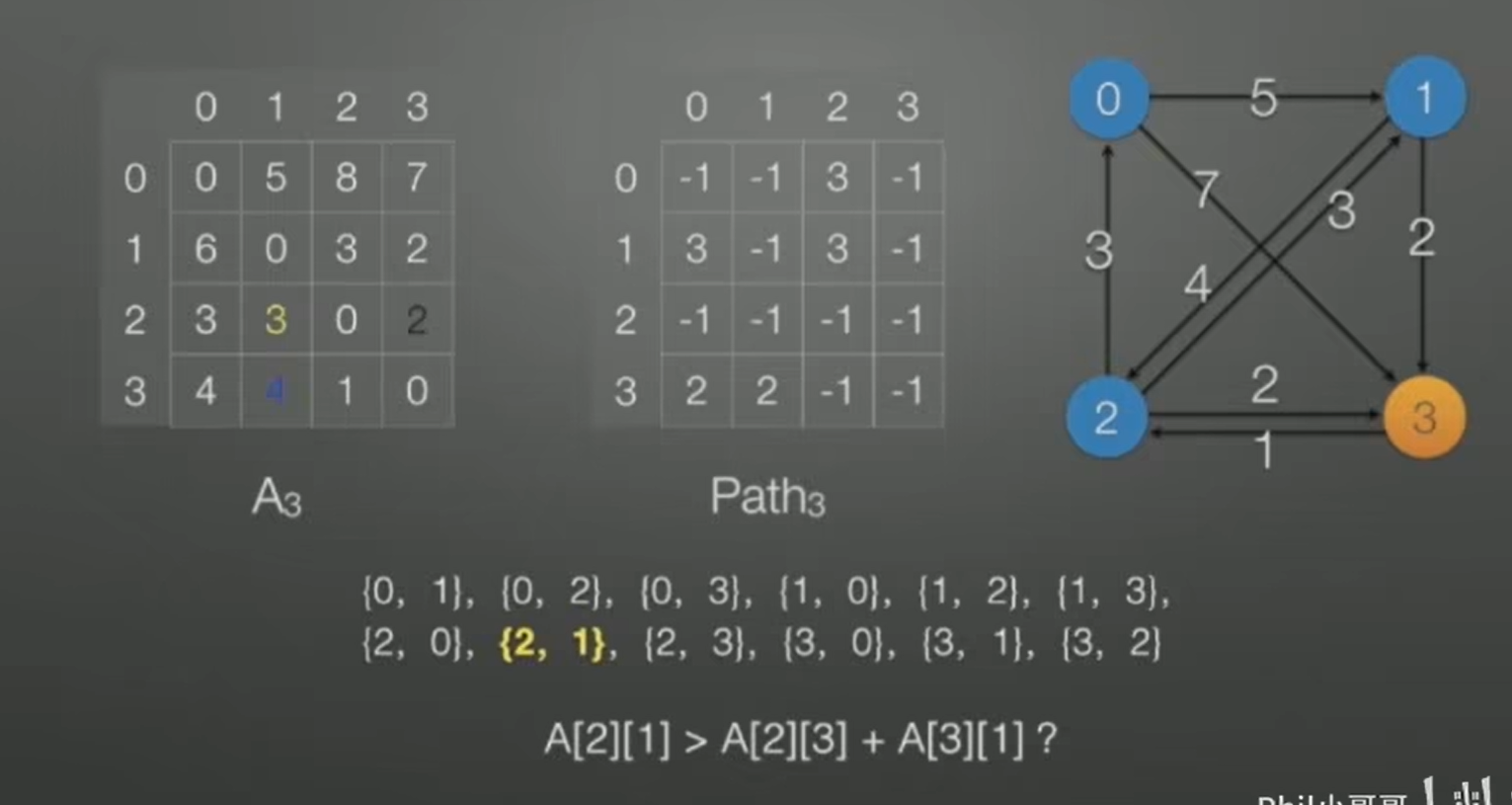
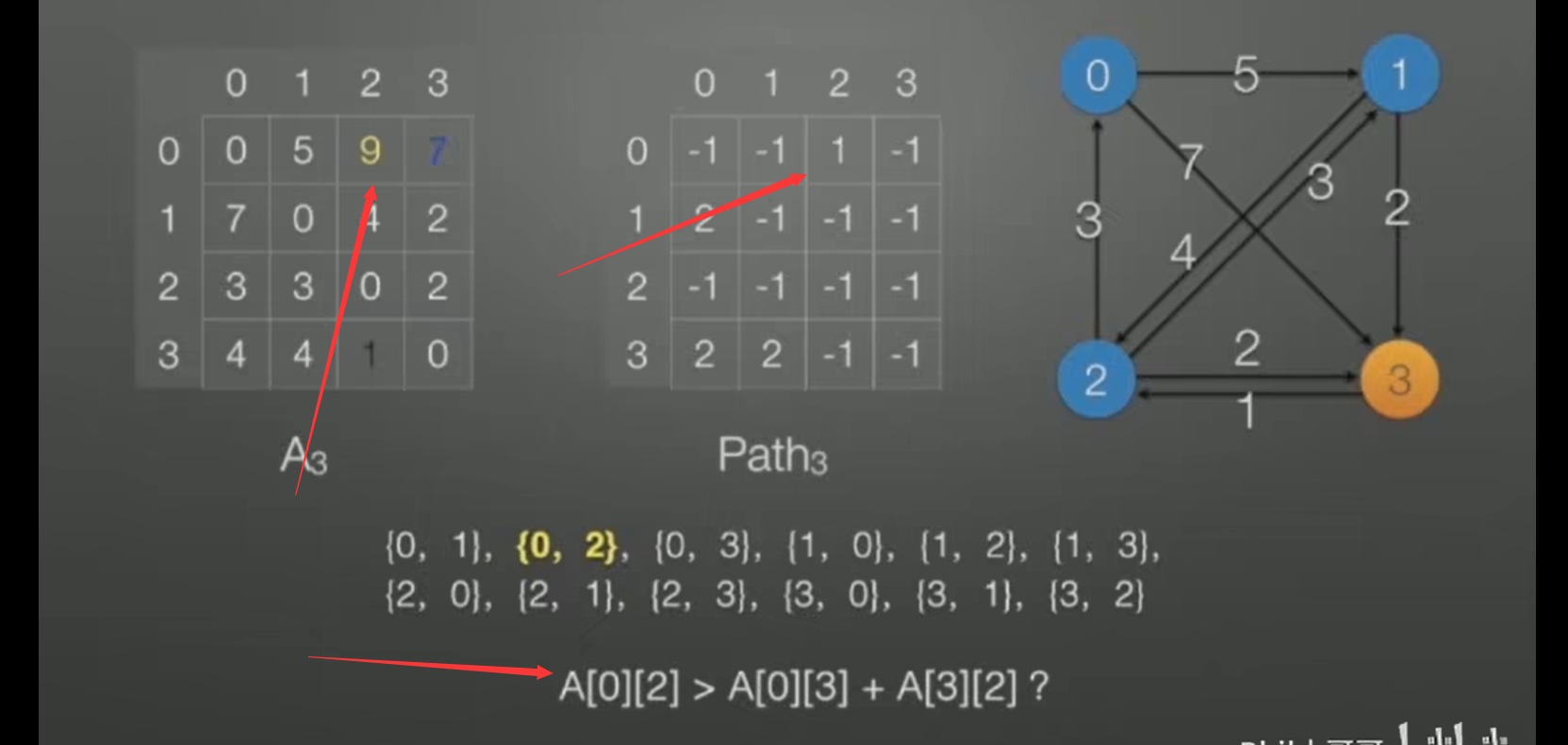
- Floyd 算法第一重循环遍历每个点,把该点作为枢轴并更新以该点为枢轴的两个点之间的最短路径,我们先从一个点来入手研究,比如我们选取点 0
- 选取点 0后,以点0为枢轴,二重循环遍历除0外的所有点,设二重循环的第一重循环参数为i,第二重循环参数为j,该二重循环遍历并比较所有的A[i][0] + A[0][j] 与 A[i][j]的大小,若前者小,则更新A_i中最短路径的大小,且更新 Path_i中的 记录的中轴节点
Path_i 表的作用: 这个表记录所有最短路径的中轴节点如" Path[0][2] = 3" 代表的含义是: A[0][2] > A[0][3] + A[3][2] ,也就是说以3为转轴的时候 节点0到2 的直接距离小于先从 0到3,再从3到2的距离和
当然,上图中是已经比较后且修改过的图,下图是比较前的图:
这个算法还是比较简单的,需要注意的是,floyd算法每次选取一个中介点,然后进行两重循环
拓扑排序
基本概念
AOV网: 顶点表示活动的网络
拓扑排序要求:
①每个顶点出现且只出现一次。
②若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。
拓展知识
拓扑排序可以判断有无环
由于AOV网中各顶点的地位平等,每个顶点编号是人为的,因此可以按拓扑排序的结果重新编号,生成AOV网的新的邻接存储矩阵,这种邻接矩阵可以是三角矩阵:但对于一般的图来说,若其邻接矩阵是三角矩阵,则存在拓扑序列:反之则不一定成立。
时间复杂度分析
- 先遍历一遍所有点,把入度为0的点压栈
- 循环出栈 (O(n))
- 把出栈的顶点所指向所有点入度减一 (O())
- 遍历这些入度减1的点,若有入度变为0,入栈
- 循环
O(e1+e2+..+en + n) = O(n)
邻接表时间复杂度为O(V+E),临界矩阵为:O(V^2)
代码
关键路径
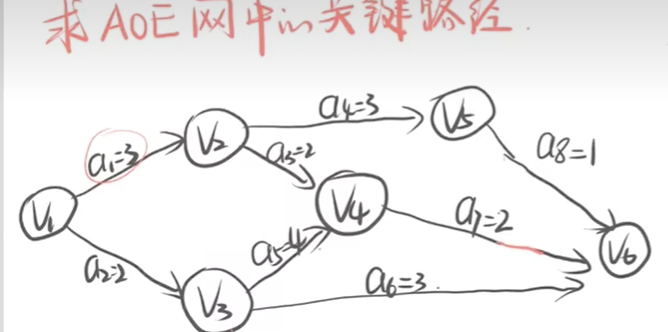
AOE网
求关键路径
1、事件最早发生时间
拓扑排序
2、事件最迟发生时间
逆拓扑排序
3、活动最早开始时间 ei
4、活动最晚开始时间 li
5、求时间余量 li-ei
时间余量为0的点为关键路径
需要注意的是求最早发生结点时,要计算指向结点的所有入度的最大值,求最晚发生结点时,要计算结点指向的所有出度的最小值,即求早取最晚,求晚取最早
时间复杂度
O(n+e)
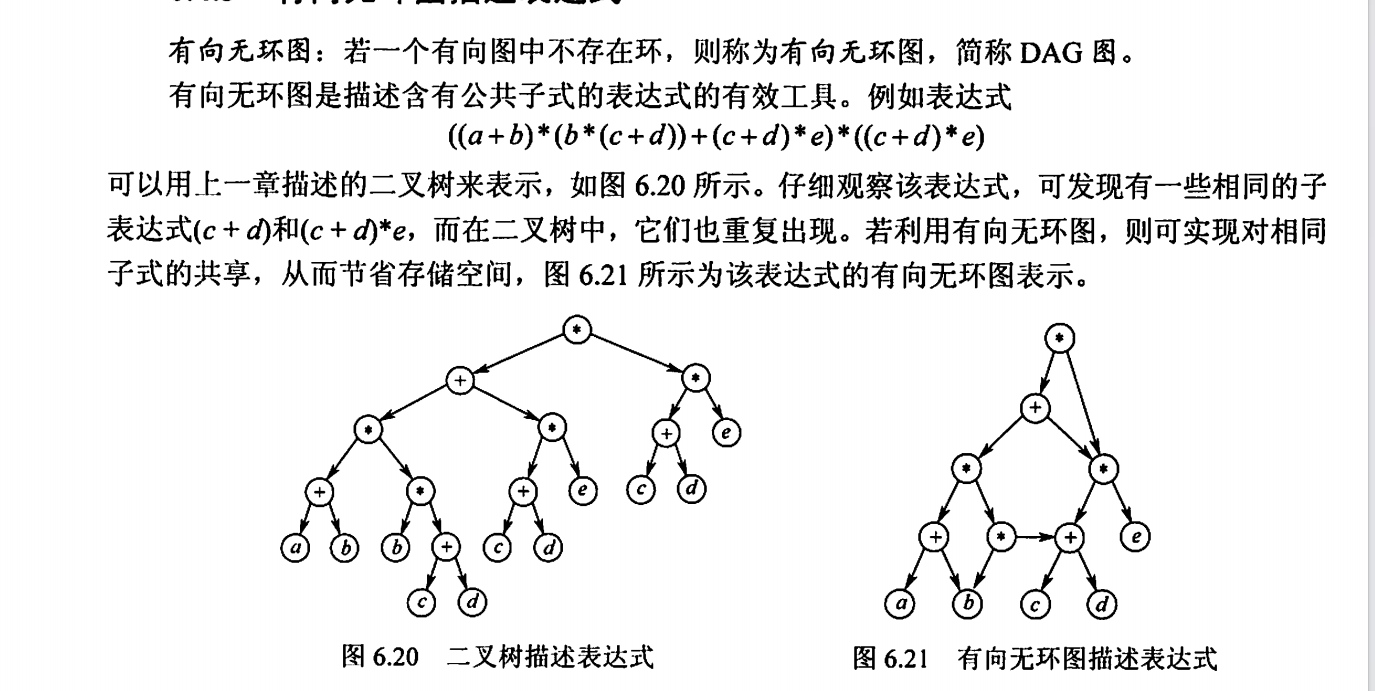
中缀表达式转有向无环图
我的感悟是先按中序建树,然后再去边
经典错题---6.4
若有向图的拓扑有序序列唯一,则图中每个顶,点的入度和出度最多为1
这句话是错误的
在图G的最小生成树G中,某条边的权值可能会超过未选边的权值
这是因为权值小的图不一定连通
总结
1、在路径序列中,顶点不重复出现的路径称为简单路径。
2、dfs算法与bfs算法发时间复杂度与空间复杂度分析
空间复杂度: O(V)
时间复杂度: O(V+E) // 邻接表法 或 O(V^2) // 邻接矩阵法
3、prim,kruskal,Dijkstra,floyd、拓扑排序、关键路径算法的时间复杂度
prim: O(v^2)
kruskal : O(eloge)
Dijkstra : O(v^2)
floyd : O(v^3)
拓扑排序: O(n+e)
关键路径: O(n+e)
4、Dijkstra 算法思路(真题常考,并且算法比prim与kruskal复杂一点,故专门记录)
-
每次从未标记的节点中选择距离出发点最近的节点,标记,收录到最优路径集合中。
-
计算刚加入节点A的邻近节点B的距离(不包含标记的节点)
若(节点A的距离+节点A到节点B的边长)<节点B的距离,就更新节点B的距离和前面点。
-
反复循环
题目中会问,当找到第n个最短路径时,dist数组的内容是多少,需要注意的是,当找到第n个最短路口路径后,需要更新一次dist,再回答题目
__EOF__

本文链接:https://www.cnblogs.com/lordtianqiyi/p/17760062.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!






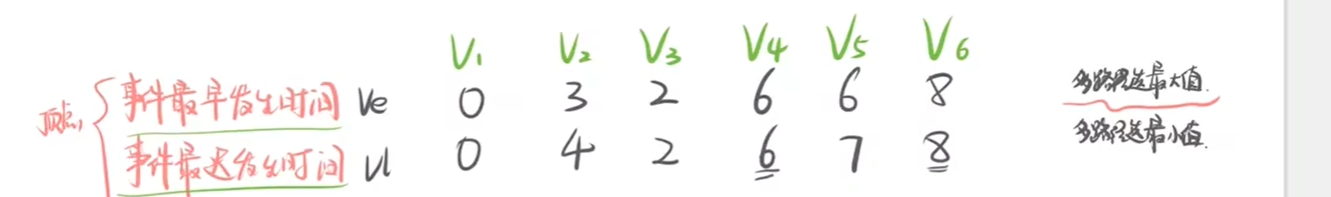



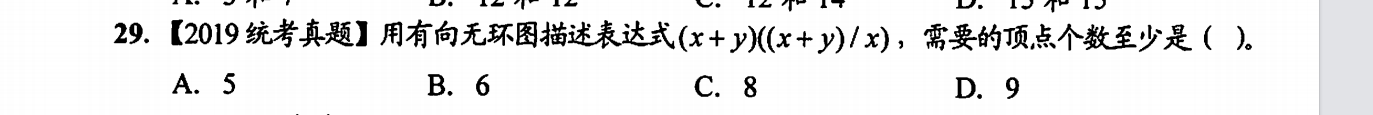



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构