王道408---DS---树、二叉树、图
有序树、无序树的概念
有序树和无序树,树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。
树/二叉树的性质
树的性质
常用的只有第一个
二叉树的性质
常用公式也只有这一个
二叉树的存储
一般分为顺序存储与链式存储
要求顺序存储能默写
顺序存储:
线索二叉树
规定:若无左子树,令lchi1d指向其前驱结点:若无右子树,令rchi1d指向其后继结点。
1、先序遍历的线索二叉树不能直接找到度为2的前驱
2、后序遍历的线索二叉树不能直接找到度为2的后继
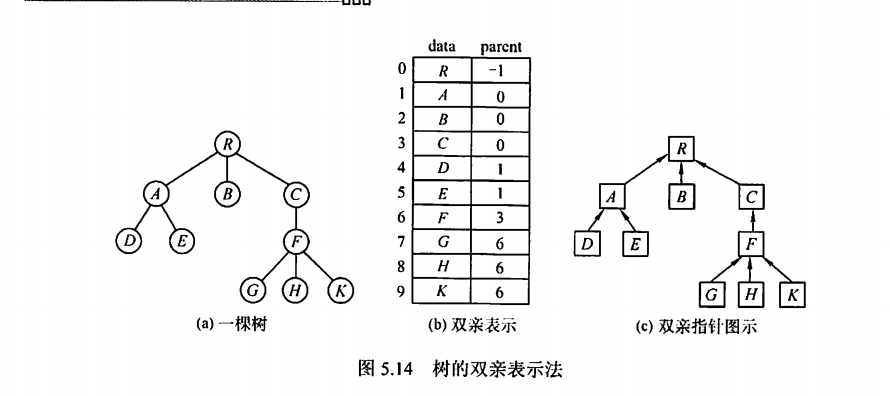
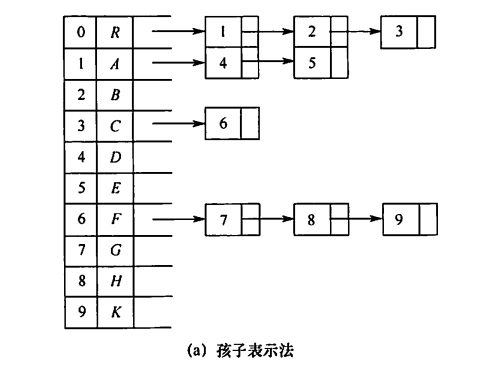
树和图的存储
二叉树的存储一般采用链表或数组
一般的树的存储手段有三种
有点像邻接表
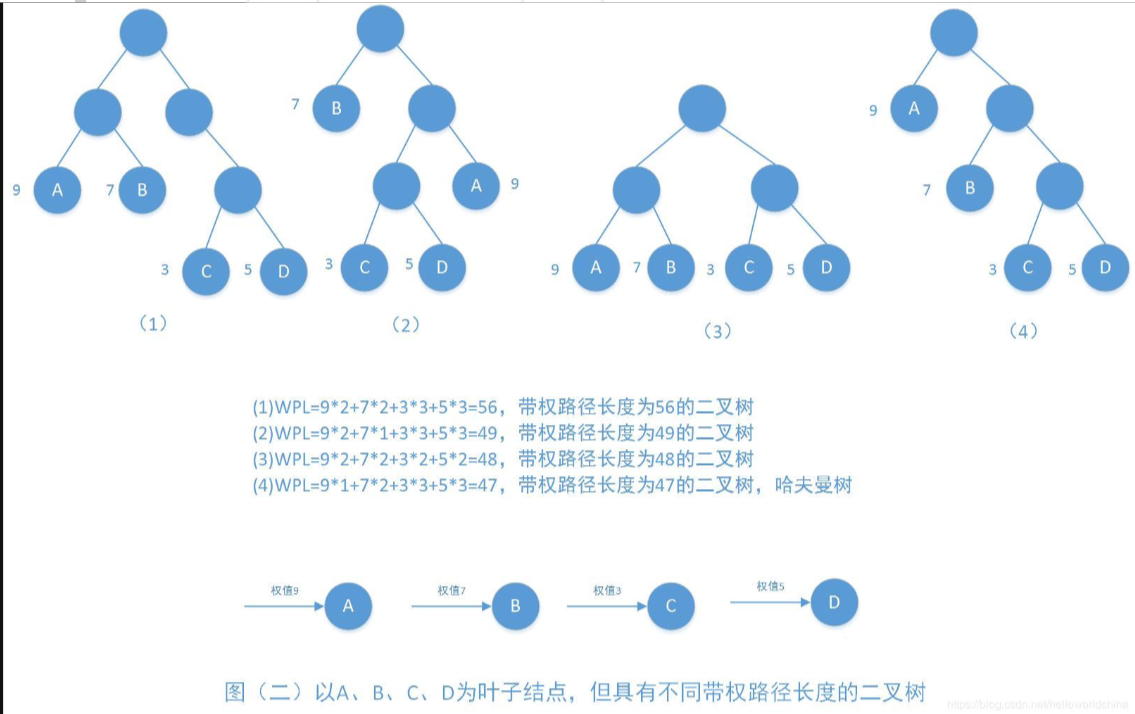
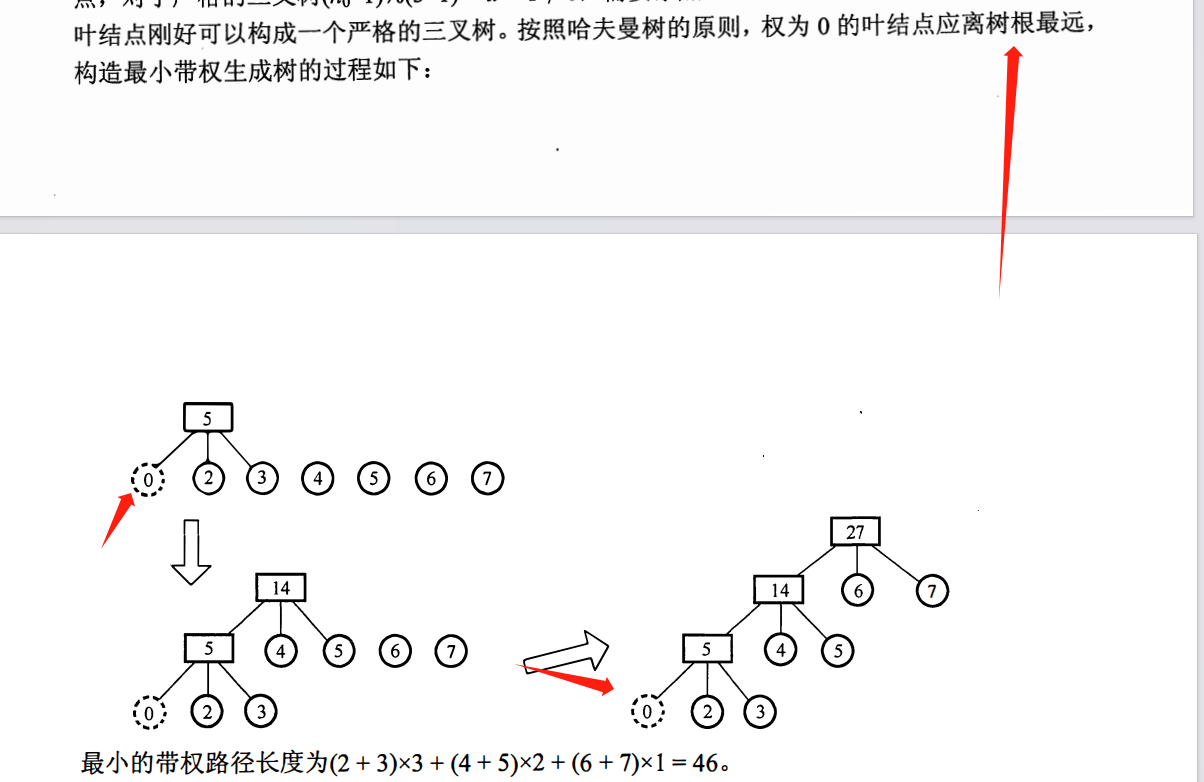
哈夫曼树的一些性质
带权路径长度的概念
在许多应用中,树中结点常常被赋予一个表示某种意义的数值,称为该结点的权。从树的根到任意结点的路径长度(经过的边数)与该结点上权值的乘积,称为该结点的带权路径长度。树中所有叶结点的带权路径长度之和称为该树的带权路径长度,记为
其中带权路径长度(WPL)最小的二叉树称为哈夫曼树
注意哈夫曼树的虚叶节点情况
哈夫曼树不一定是是一棵完全二叉树
树中一定没有度为1的结点
树中两个权值最小的结点一定是兄弟结点
树中任一非叶结点的权值一定不小于下一层任一结点的权值
计算机网络中A,B,C类网络的划分以及动态子网的划分,其思想与哈夫曼编码如出一辙
并查集
代码
自从大纲改版还没考过,感觉今年很可能考,这是个重点!最次也要会默写朴素算法的并查集
代码如下(涉及了路径压缩、小树合并到大树等优化策略)
朴素算法代码如下
优化方案
朴素算法
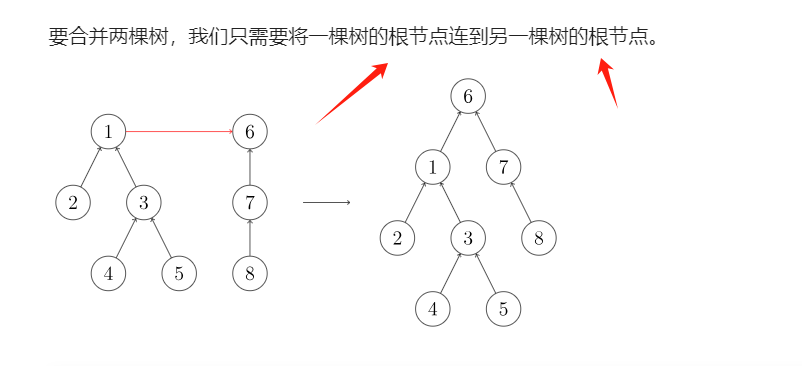
加入存在集合A与B
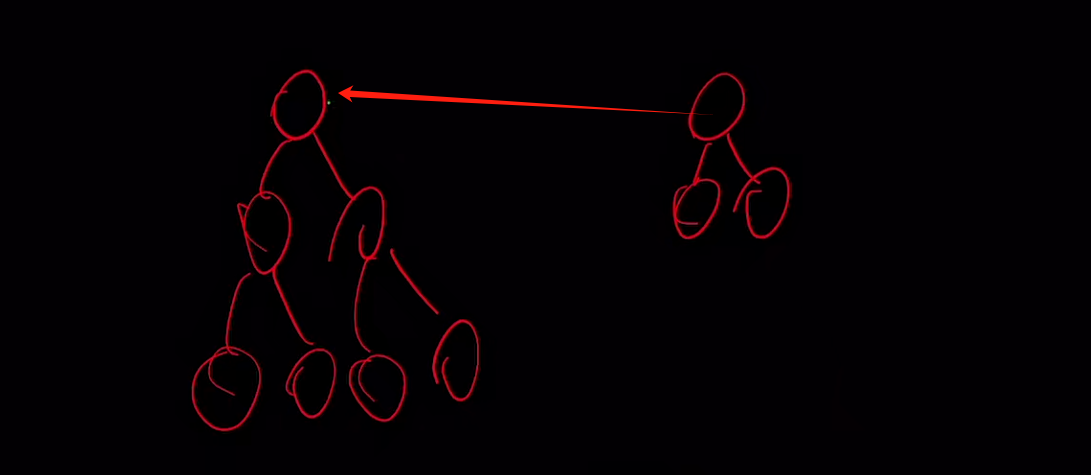
每次Union的时候,都会使集合B的根节点指向集合A的根节点:
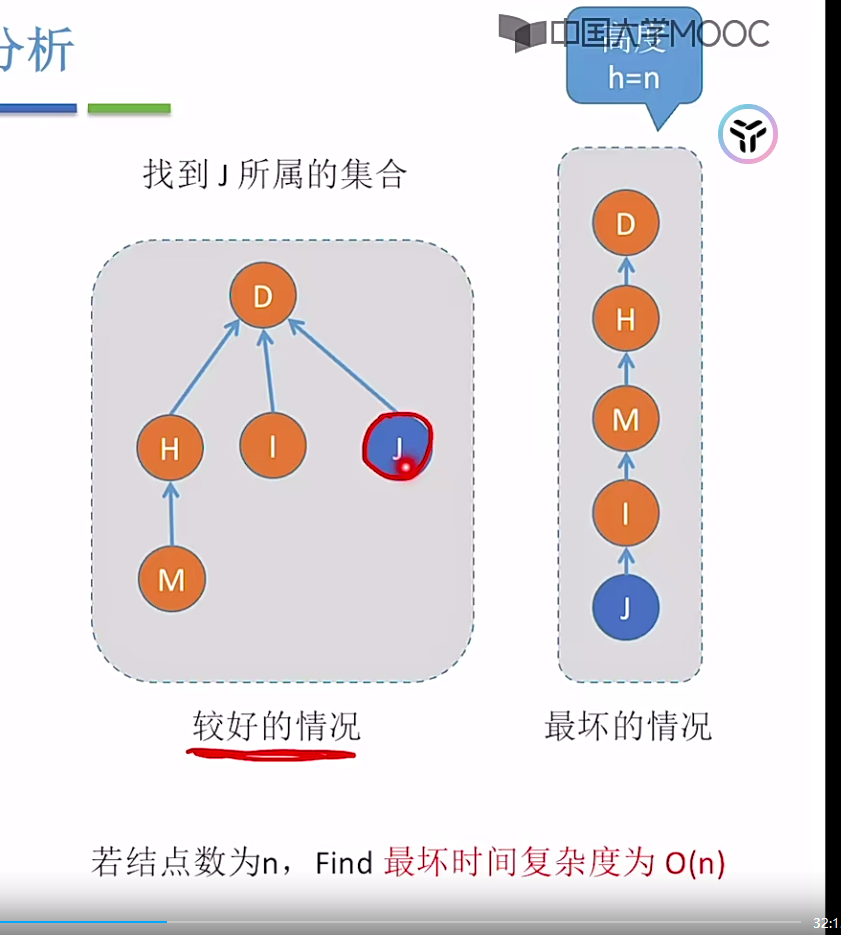
对于朴素算法的Find函数,最坏的时间复杂度可能到达O(n)
树高越高,Find操作的时间复杂发也就越大
那么我们的优化思路就是,尽量减小树的高度:
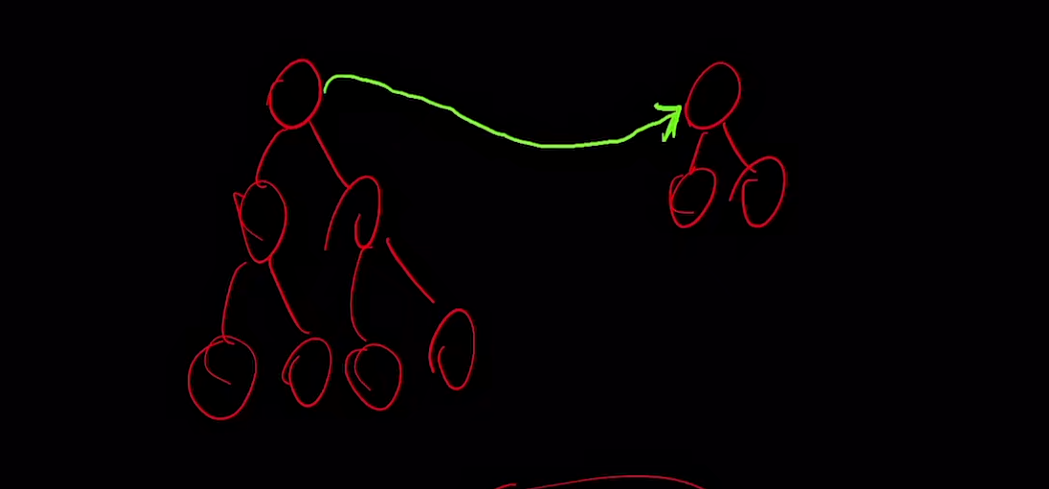
小树合并到大树的优化策略---对Union优化
我们可以直观的感受一下,如果我们用大树合成到小树上,会发现整体树的高度会加1
如果我们用小树合成到大树上,会发现整体树的高度不会改变!
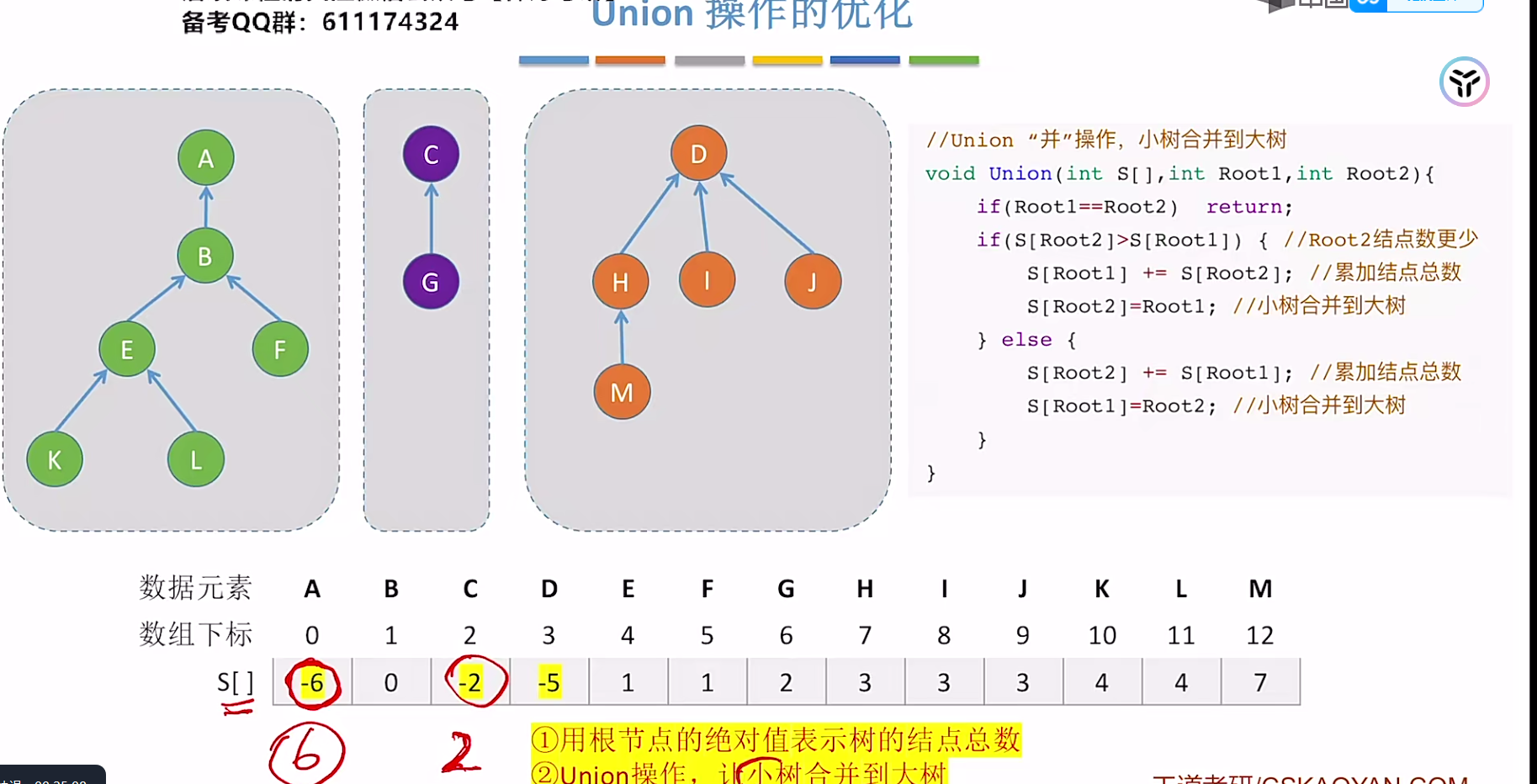
那么我们可以在每次Union的时候都让小树指向大树,为此我们需要用一个值来表示树的结点总数
我们选取根节点的绝对值作为结点总数:
这样优化之后会使整个树的高度不超过 (注意如果M不是整数,⌊ M ⌋ + 1 != ⌈M⌉ )
这样就可以保证的时间复杂度
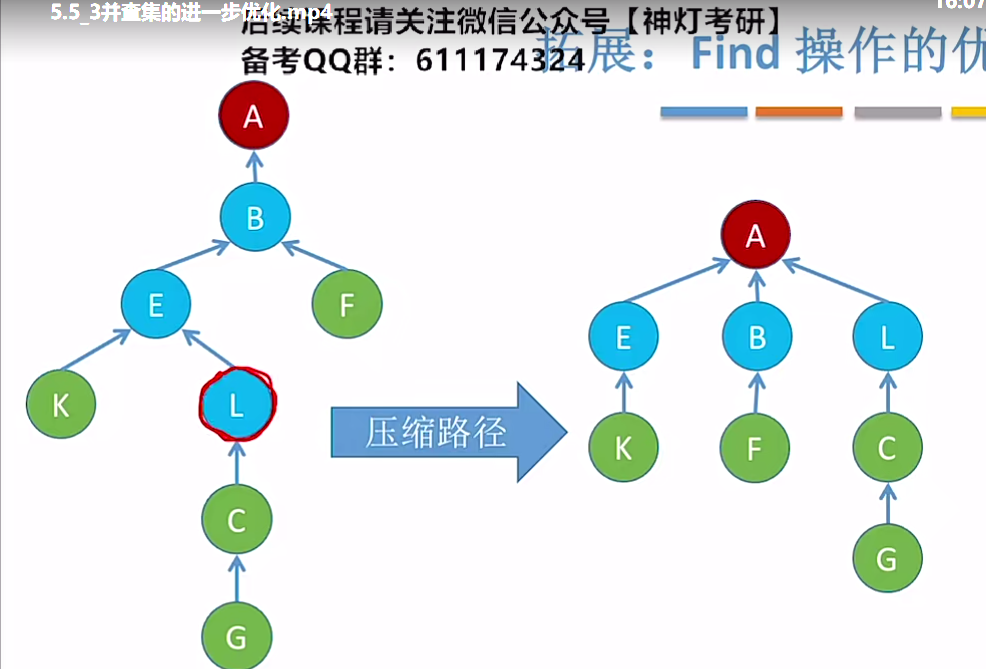
路径压缩---对Find函数的优化
压缩路径---Find操作,先找到根节点,再将查找路径上所有结点都挂到根结点下
代码如下:
每次Find操作,先找根,再"压缩路径",可使树的高度不超过O(α(n)). α(n)是一个增长很缓慢的函数,对于常见的n值,通常α(n)≤4,因此优化后并查集的Find、Union梁作时间开销都很低
另外find的功能是这样的:
在把1合并到6结点的时候可以发现,find函数并不是把1所在的子树的所有结点都连接到6结点下,而是先把1所在子树的结点都指向1所在子树的根,再把根指向6所在结点的根
算法复杂度分析
朴素算法
一次Find 最坏时间复杂度 : O(n)
总体是O(n^2)的时间复杂度
小树并到大树
一次Find 最坏时间复杂度 :
总体是 :
路径压缩
一次Find 最坏时间复杂度 : O(α(n))
总体是 : O(n · α(n))
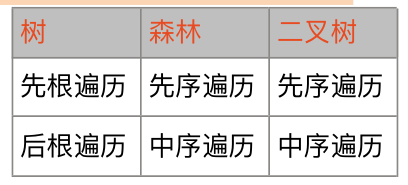
树、森林、二叉树遍历对应关系
这里需要注意的是
- 树的后根遍历相对于树来说是后序遍历,相当于其对应的二叉树来说是中序遍历
- 森林的中序遍历实际上是对森林后序遍历,其结果等价于对应二叉树的中序遍历,不知道为什么给起了一个中序遍历的名字,可能是其无法进行真正的中序遍历的原因吧
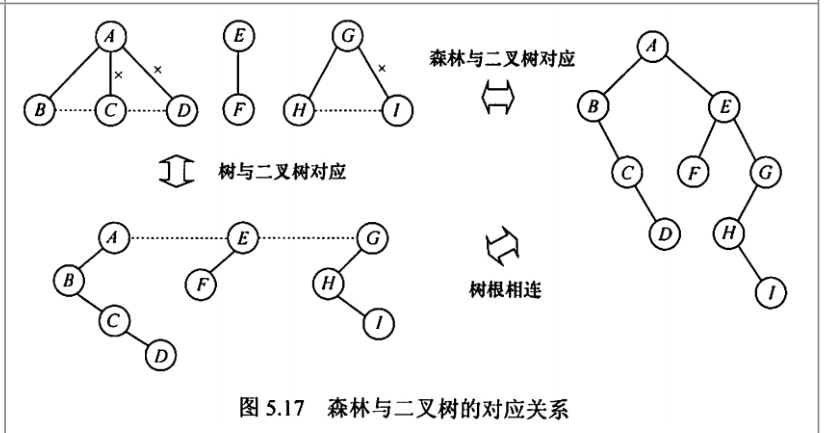
如图:
对森林中序遍历(实质上是后序遍历)可得到 BCDAFEHIG ,等价于对二叉树的中序遍历
__EOF__

本文链接:https://www.cnblogs.com/lordtianqiyi/p/17760058.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!


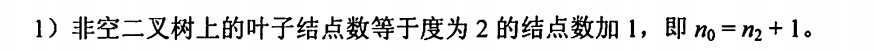




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 25岁的心里话
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现