math---记录冲刺阶段的各种问题以及一些错题
一、二维平面下的积分(包括直角坐标系、极坐标、参数方程的下的面积、弧长、侧面积和体积公式以及一些拓展)
问题来源: 2003年数二真题填空题第四题开门红
这道题极其的简单,却折射出了我的很多问题 我发现我对极坐标下的各种积分都有很大程度的遗忘,有的积分公式甚至一点印象都没有,如同没学
1、直角坐标系、极坐标、参数方程下的面积公式
注意这里的极坐标面积公式!!!
2、直角坐标系、极坐标、参数方程下的弧长公式
3、直角坐标系、极坐标、参数方程下的旋转体表面积公式

对于极坐标与参数方程的表面积公式,实际上就是先列出直角坐标系的公式,再把极坐标或参数方程套进去,仅此而已,需要注意的是dx已经提前带了进去,不要再代
4、直角坐标系、极坐标、参数方程下的旋转体体积公式
这里说一下几个点
- 参数方程的体积公式其实就相当于直角坐标系的体积公式下灌入参数方程
- 极坐标的体积公式还可以这样写:

直接把极坐标方程化成直角坐标系(参数方程)的形式,然后在用直角坐标系的方式对其积分,在积分过程再次化为极坐标!!!
这种方法十分便以理解 - 极坐标体积公式不好推导,直接记下吧
5、我们在学二重积分时,对坐标区域使用极坐标变换的手段与上面的求极坐标面积公式大不不同,前者一般是用固定的极坐标变换(x=rcos,y=rsin)对已给出的直接坐标系进行拟合,它本身不是极坐标,而是要后天变成极坐标
-
一般来说转化成参数方程要比转化成极坐标好求
如: 计算的弧长
这个转化成极坐标简直无从下手,但转化成参数方程则一目了然
6、我们在学习三重积分的时候也经常使用极坐标变换,这里的极坐标变换大致分为这样几种
- 使用极坐标对已给出的空间直角坐标系进行拟合
- 球的体积公式,或者类球的体积公式(指能通过雅可比变化成球)
这里的三重积分有一种独特的手段:可以根据直角坐标系直接写出其参数方程

同样,这种手段也可以用在二维平面上:
求的面积,我们既可以直接使用极坐标拟合,也可以直接化成参数方程来求解
7、对于某定长直线的旋转体体积的求解
这是一个容易忽视的问题,张宇老师给出的公式又臭又长,凯哥给的公式有使用范围,武老的公式算是万能
具体看:
https://www.cnblogs.com/lordtianqiyi/p/17578154.html
二、简化三角函数/把三角函数化为不含三角函数的最简形式
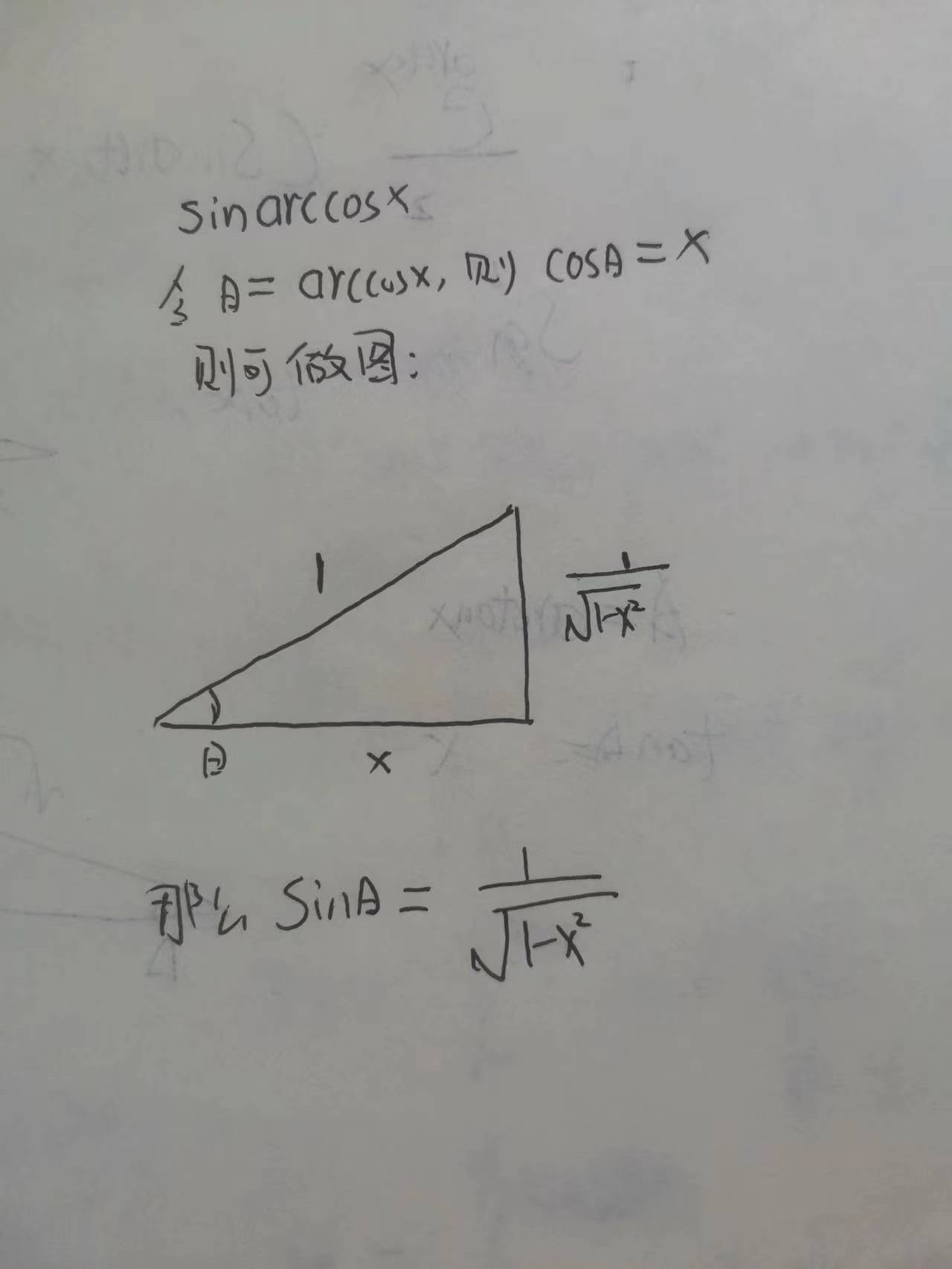
如: sin(arctanx)
https://math.stackexchange.com/questions/2714044/expressions-for-sin-arctanx-and-cos-arctanx-that-do-not-contain-tr
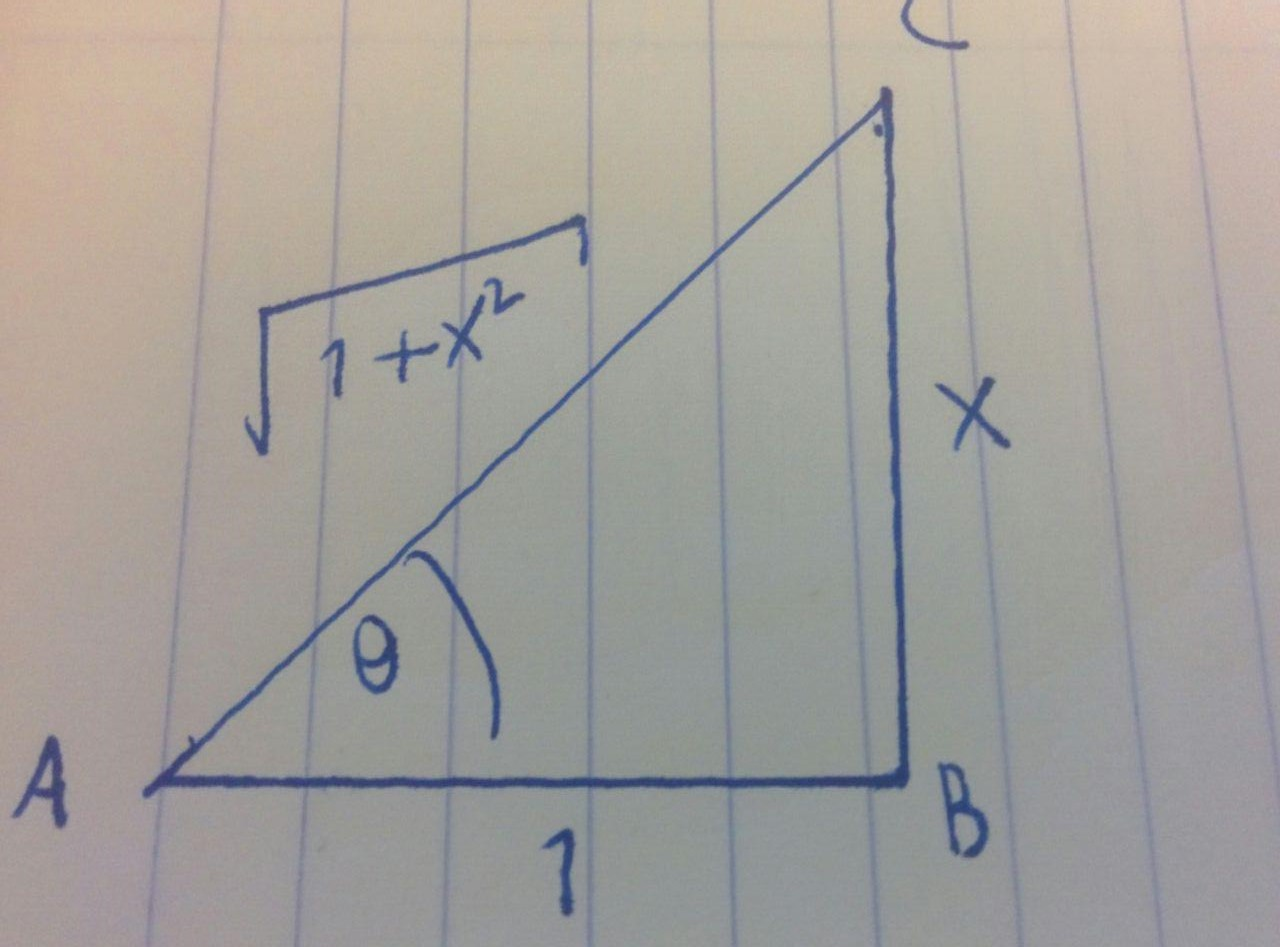
再如 sin(arccosx)
三、反函数求导
问题来源: 2003年数二真题第六大题
函数与反函数的转化公式忘记了,同时12points

反思了一下,记不住公式的原因有两点:
1、宇哥给的公式是从前往后推的,也就是通过对(正)函数求导来得到反函数公式,这导致我在看到这个题目时,一时没有想到用反函数转化公式

四、n与x的动静结合问题
问题来源: 数二660-T444和2004年数二第一题
之前一直都没弄明白的一点: x是在连续的改变还真正的只是参数的变化
题源刨析
关键要点
当x趋于0+时,(n-1)的结果是->∞的,当x等于0时,其结果是等于0的;一直困惑我的一点在于,当x从0+到0逼近的过程,会不会像函数一样连续的逼近,直至到0,事实上,x仅仅作为常数,无论他多逼近于0,它还是会等于无穷
如果明白了这一点,这两道题就会变得很简单
五、函数连续但导数不连续的经典例题(x)
题目来源-2004-数二-T10
解题关键
关键就是要知道,函数连续不代表导函数连续,也就是说,题目中f'(0)>0,但如果题目没有说明导函数连续,那么在0的去心领域,β=(0-γ,0+γ)中,f'(β)未必大于0,如以下函数:
(经典反面案例,还是背下为好

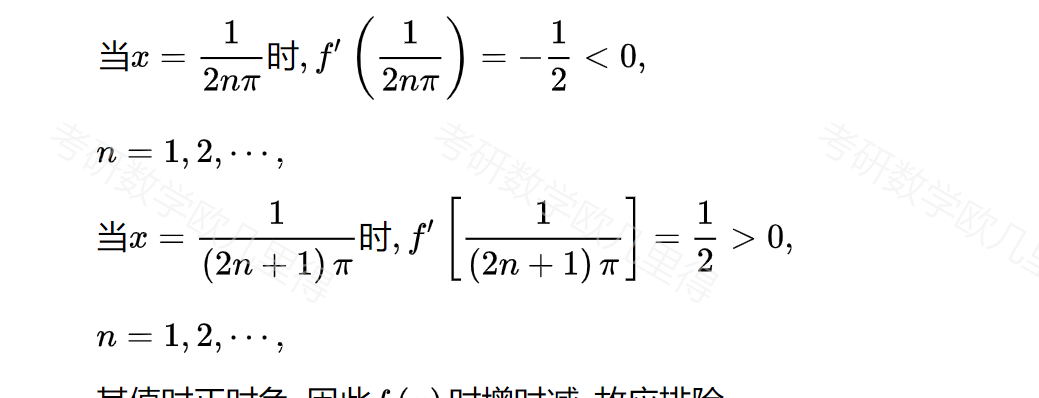
六、行向量组列向量组、行满秩列满秩的应用---知识点强化
这一块一直掌握的不太好,归根到底,在于定义掌握的不准确,今天可让我遇到相关的题了
题目来源-2004数二-T14
解题关键/知识点回顾
1、首先介绍一下行满秩与列满秩

2、列向量组线性相关的概念
实际上就是把一列看着一个列向量,看这几个列向量能否线性表示即可
3、这道题的解题关键在于这个定理:

需要注意的是,这里的A、B矩阵不是方阵!!!
4、先回顾一下这两个定理的证明方法:

关键就是3中提到的公式的运用
那么这道题的解题步骤如下:
r(A)<n,且A是m行,n列矩阵,那么就一定说明A的列不满秩(行不满秩无法判断,因为不知道m与n的大小关系)
同理,可证B
另一种另类的思路
七、有理函数的积分+留数法
问题来源 : 2009年-T16,求最后的有理函数积分时用了太多时间
留数法:
需要注意第三种情况
七、极坐标变换提前把r赋值的问题
题源刨析
最常规的一类题了,byd这都能做错,给我气死了
经典的错误
正确做法:
问题出在了积分变换上 :
假如我们对进行积分, 前者积分的时候相当于对整个积分区域积分,而后者积分的时候只是相当于对r0这个曲线积分
我真的希望我不要再错了
八、拉格朗日的证明
题源刨析
会做第二问,不会第一问,乐
方法一 标准的做法 构造函数法
这种标准做法略显突兀,很难想到
方法二 K值法
私以为这样做和第一种方法很像
方法三 另一种构造函数法
这种方法好一些,容易接受
九、矩阵A能被矩阵B线性表示
题源刨析
2011年-T22
知识点
设三维矩阵A包含列向量组 ,矩阵B包含列向量组 () ,并且A不能表示B其等价命题有:
又 不能由 表示出来,所以可得:
若 ,则表示 可由 线性表示,
,表示 可由 线性表示,
, 表示 可由 线性表示,
=>
表明 同时被 表示了出来
十、极值点的寻取
题源刨析
2003年-T10
知识点
找极值点先找驻点和不可导点
,是f(x)的驻点。
对于不可导点,若点的邻域左右导数异号,则为极值点。
可导<=>左右导数均存在且相等
很显然在题目中x=0的邻域内出现了左右异号,故为极值点
十一、拐点解法刨析
题源刨析
题1是 2004-T8
题2是 2011-T3
解法一---一阶导法
求出一阶导 f'(x) ,之后根据f'(x)的图像进行计算拐点个数,只要左右领域异号就是拐点
这个方法在某些情况下不很好用
解法二---二阶导法
直接求二阶导f''(x) ,判断是否过x轴即可
在一些具有绝对值的函数下不好用
解法三---纯图像法
这个方法才是我想讲的,速度快,效率高
前要知识
我们研究一下y=x^2 、 y=x^3与 y=sinx的图像:
可以发现当f(0)处的位置,图像千差万别,f(x)=x^2 与 f(x)=x^3 在x=0的邻域内左右都是凹函数,而f(x)=sinx 在x=0的领域内左右都是凸函数,这也是我们下文用来判断拐点的依据
求解题1
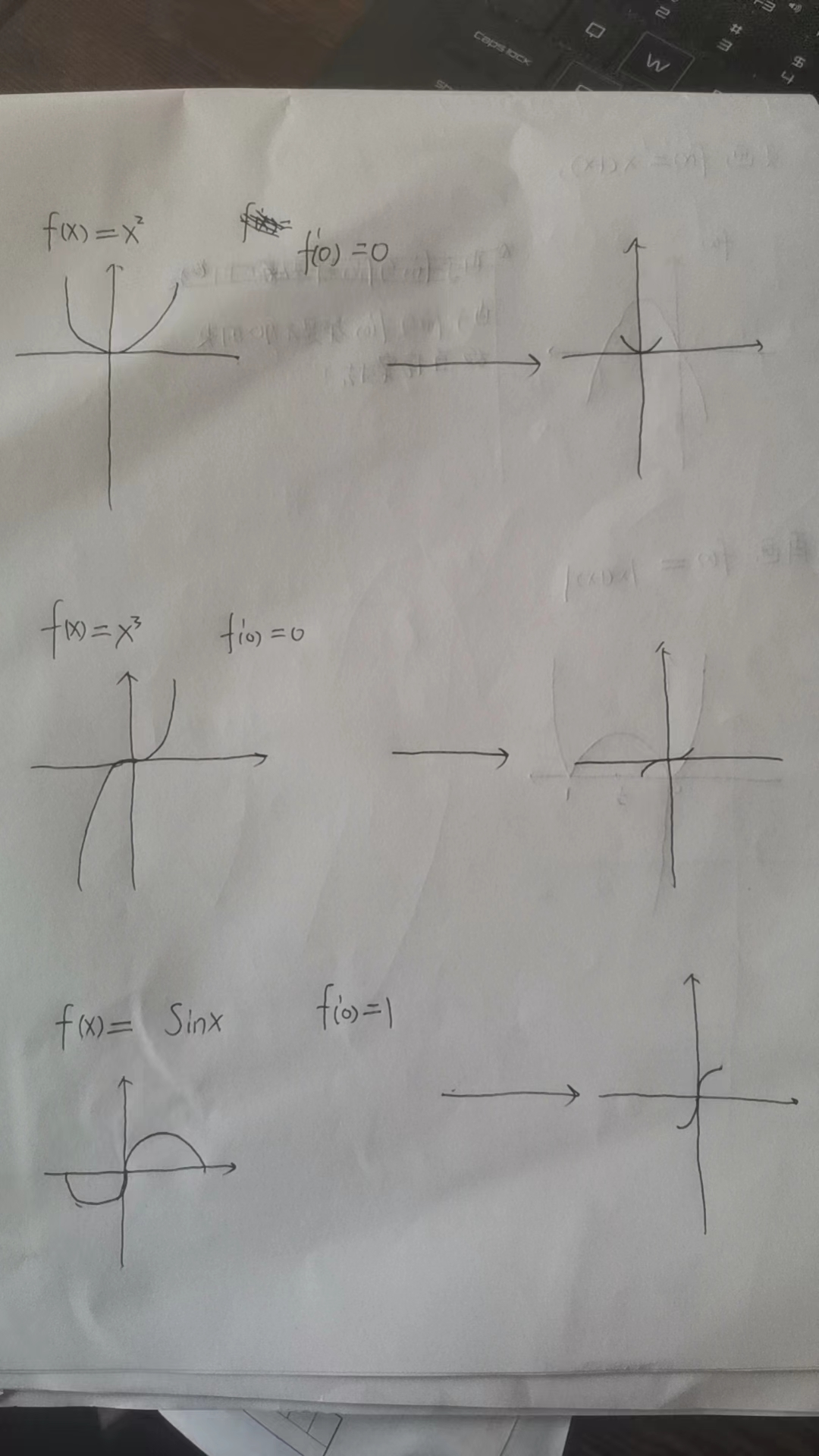
直接画图,根据图像判断
比如 f(x) = |x(1-x)|这道题:
我们显然发现在 f(x)=x(1-x)下f(0)与f(1)的左右领域都类似于凸函数,而经过翻转,翻转成f(x)=|x(1-x)|后,f(0)与f(1)的左右领域中出现了一凹一凸的情况,即这俩都是拐点
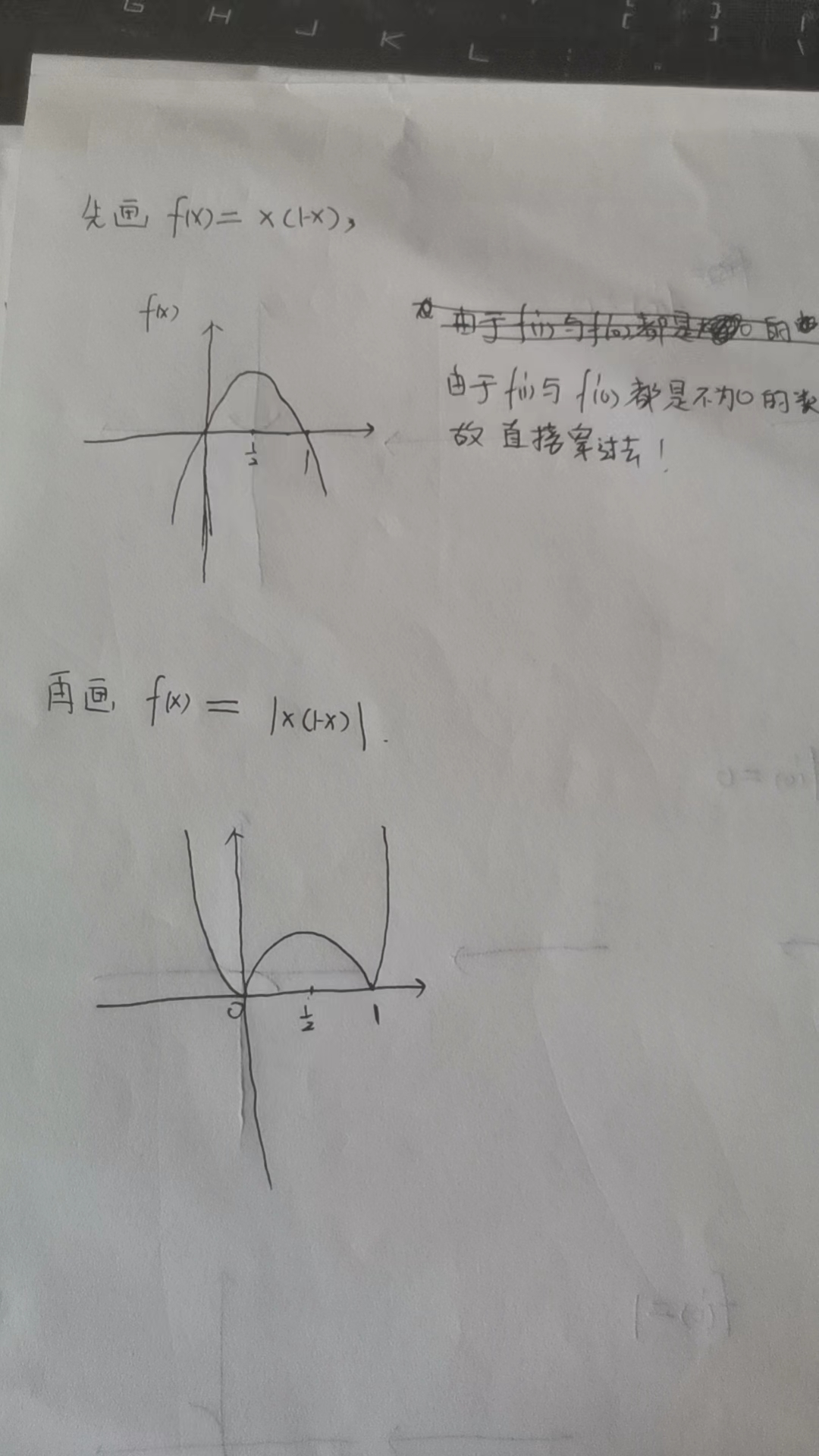
求解题2
没啥好说的,直接上图
秒了
十二、根据全微分方程求解全微分的方法---(全微分法、不定积分法、特殊路径法)
张宇当时一笔带过,导致我当时没有学的很明白,如今几道题目把知识点串了起来
题源刨析
1、660-T224
2、2009-T3
3、2012-T12
4、武神---强化328题
全微分做法
全微分做法的原理就在于这个公式:
以T3为例
T4:
不定积分做法
这个方法的原理是使用了这个公式:
以T1为例
T3
特殊路径法
积分与路径无关
核心公式
当满足上面的条件时,就可以使用特殊路径法
需要注意的是,特殊路径法中的计算细节需要拿捏的准
如T3
最好就是按题目的 P(x,0) + Q(x,y)这样写!!!不会出现问题的
十三、错误的不可逆的配方法
我们做题的时候会看到题目配方已经配好了,却还让我们求规范性或者标准型;这是老头的坑,它给的都是错误的不可逆的配方方式
题目朔源
2023-T9
2018-T22
知识点
以2023-T9为例
题目中的配方方法是这样的:
转化为矩阵为:
其行列式值为0,而我们在进行配方法的时候会出现 转 的情况,也就是说要求矩阵线性变换可逆
而题目中的线性变换不可逆,所以我们得换一种配方方法...
__EOF__

本文链接:https://www.cnblogs.com/lordtianqiyi/p/17741178.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!




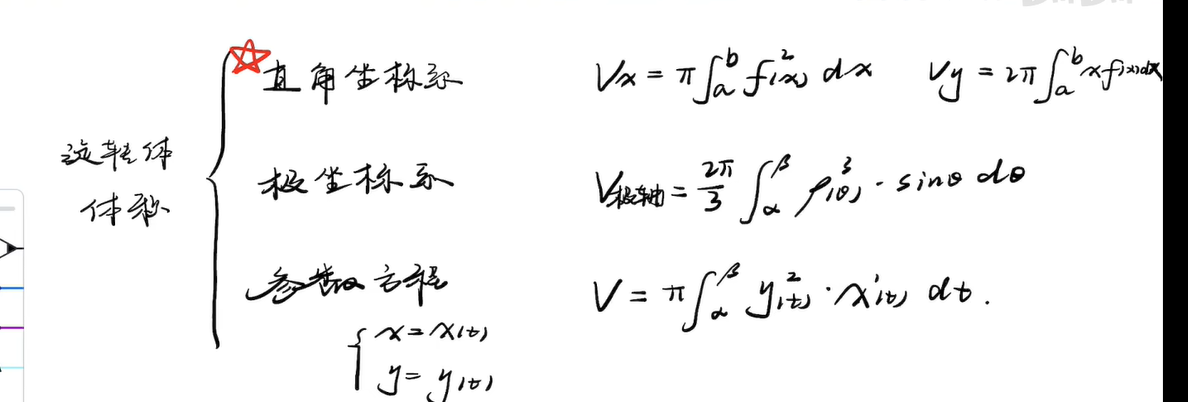
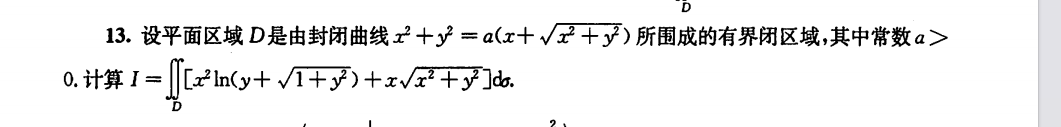





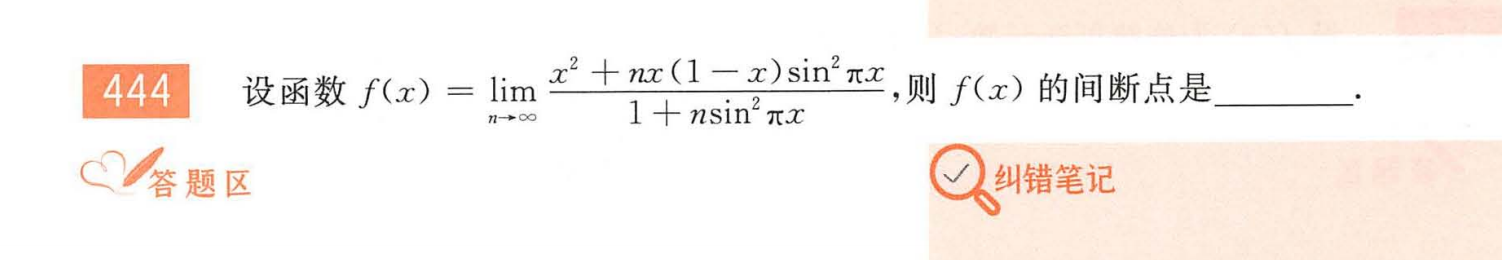




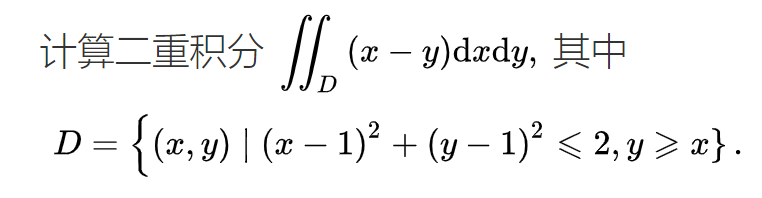











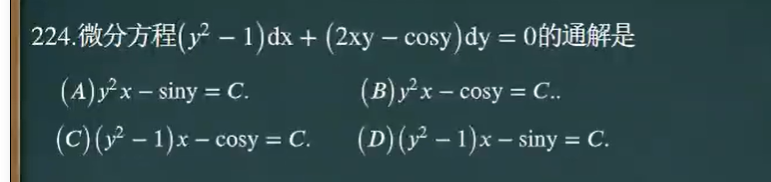



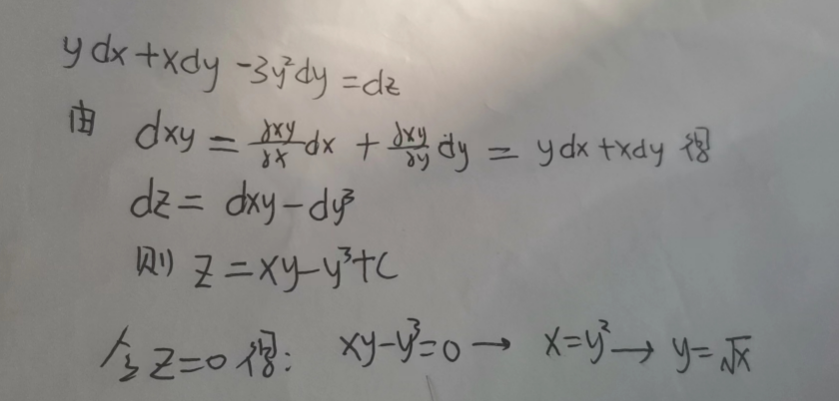
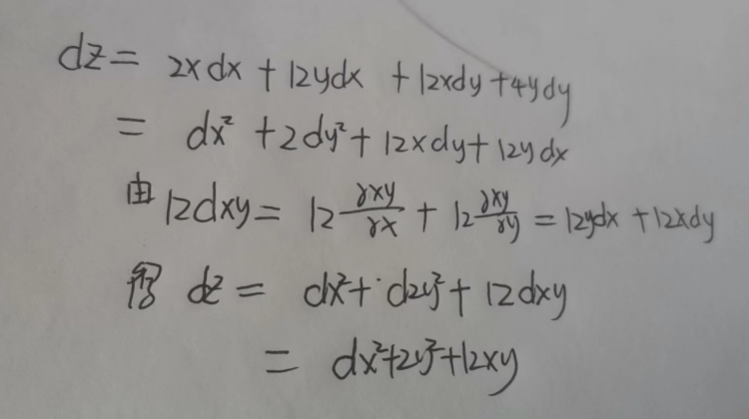
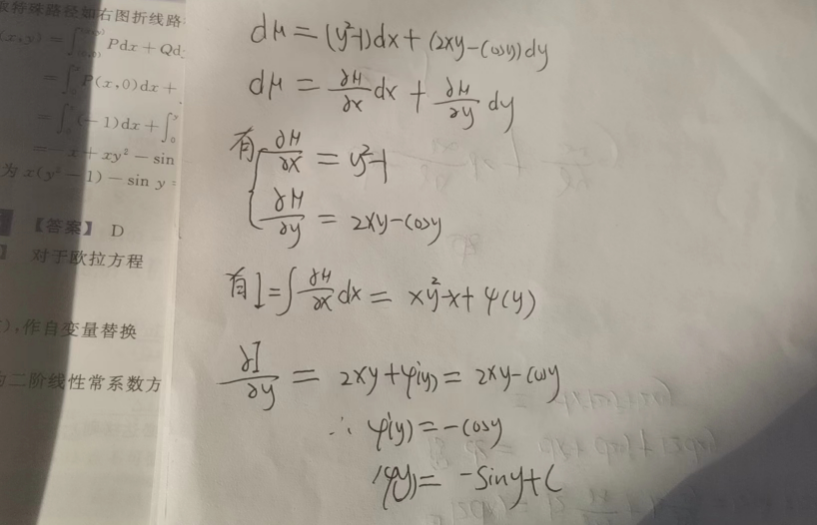






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 25岁的心里话
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现