math---多维随机变量函数的求法(截至目前已知的方法) 以及 卷积公式原理
前言: 感觉这里的知识有点小乱,遂浅浅整理一下
零、卷积公式法原理
卷积公式法的原理其实就是分布函数法+暴力求导公式
首先介绍暴力求导公式:
1)、常规的,列出求Z的分布函数公式: p(Z<=z) = p(X+Y<=z)
之后,我们把
看作g(z,x),下面就是对g(z,x)做从负无穷到正无穷的定积分
2)、直接使用暴力求导公式
暴力求导公式中的后两项由于g(z,x)的上下限为常数(正无穷,负无穷也算常数吧),则其导数值为0
暴力求导公式的第一项
需要对 g(z,x)求关于z的偏导,则求完偏导后,该项变为:
整理可得:
一、(连续型,连续型) =>连续型
常规的做法有:
1、分布函数法
分布函数法经常会遇到事件不独立的情况,我们一般的采取措施是
1)、换元出公共变量,划分图像
2)、直接带到图像里去
这道题的第二问就是构造出 x<=z,y<=z的情况,然后根据图像进行积分
2、卷积公式法
卷积公式法有时候也会遇到限制:
比如这道题,如果我们替换x,则会出现z的范围不好确定的情况
但如果替换y的话,就可以顺利解出
总之,还是适用分布函数法比较好,毕竟卷积公式也是起源于分布函数法
3、非常规方法---全概率公式法(适用范围较窄)
化为全概论公式后,用积分的方式来合并所有项
二、(离散,连续) => 连续
这种一般使用全概率公式就能解,面对一些不独立的题目则需要带入图像或换元出公共变量来进行积分求解
三、剩下两种都很简单,无需多言
__EOF__

本文作者:_TLSN
本文链接:https://www.cnblogs.com/lordtianqiyi/p/17729584.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/lordtianqiyi/p/17729584.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!






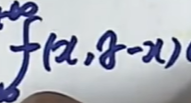







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 25岁的心里话
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现