深度学习和神经网络-深层神经网络
1.深层神经网络(Deep L-layer neural network)
在前面的内容中,我们学习了只有一个单独隐藏层的神经网络的正向传播和反向传播,还有逻辑回归,并且还学到了向量化(这在随机初始化权重时很重要)
现在我们要将这邪恶理念集合起来,用来执行我们自己的深度神经网络。在过去的几年里。DLI(深度学习学院deep learning institute)已经意识到有一些函数,只有非常深的神经网络才能学会,而浅层的模型则办不到。尽管对于任何给定的问题很难去提前预测到底需要多深的神经网络,所以我们可以先尝试逻辑回归,尝试一层然后两层隐含层,然后把隐含层的数量看作是另一个可以自由选择大小的超参数,然后在保留交叉验证数据上评估,或者用开发集来评估。
我们再看一下深度学习的符号定义:
上图是一个四层的神经网络,有三个隐藏层。我们可以看到,第一层有五个隐藏单元,第二层有五个,第三层三个。我们用L表示层数,上图中:L=4,输入层的索引为“0”
,第一个隐藏层n[1]=5,表示有五个隐藏神经元,同理,n[2]=5,n[3]=3,n[4]=n[L]=1(输出单元为1)。对于输出层,n[0]=nx=3。在不同层所拥有的神经元的数目,对于每层都用a[l]来记作 l 层激活后结果,我们会看到在正向传播时,最终我们可以计算出a[l]。通过激活函数g计算z[l],激活函数也被索引为层数l,然后我们用w[l]来记作在l层计算z[l]值的权重。类似的,z[l]里的方程b[l]也一样。
最后总结符号约定:
输入的特征记作x,但是x同样也是0层的激活函数,所以x=a[0]。
最后一层的激活函数,所以a[L]时等于这个神经网络所预测的输出结果。
2.前向传播和反向传播(Forward and backward propagation)
前向传播 :输入a[l-1],输出a[l],缓存z[l];从实现的角度来说,我们可以缓存w[l]和b[l],这样更容易在不同的环节中调用函数。
所以前向传播的步骤可以写成:z[l]=W[l]*A[l-1]+b[l] A[l]=g(Z[l])
前向传播需要提供A[0]也就是X来初始化;初始化的是第一层的上输入值。a[0]对应于一个训练样本的输入特征,而A[0]对应于一整个训练样本的输入特征,所以这就是这条链的第一个前向函数的输入,重复这个步骤就可以实现从左到右计算前向传播。
下面是反向传播的步骤:输入为da[l],输出为da[l-1],dw[l],db[l]

所以反向传播的步骤可以写成:

用向量化的方法可以写成: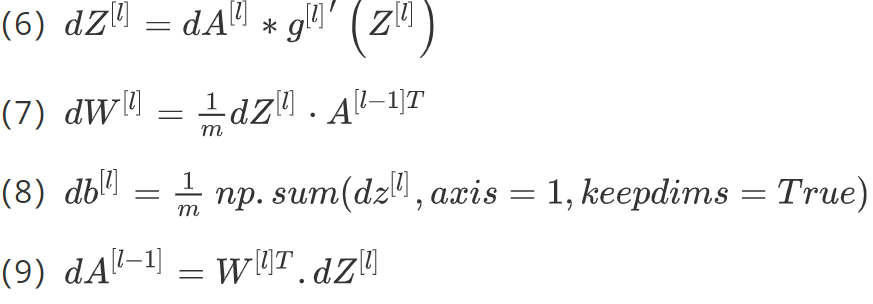
3.深层网络中的前向传播(Forward propagation in a Deep Network)
我们先来看对其中一个训练样本x如何应用前向传播,之后应用于向量化的版本。
第一层需要计算z[1]=w[1]x+b[1], a[1]=g[1](z[1])(x可以看作a[0])
第二层需要计算z[2]=w[2]a[1]+b[2], a[2]=g[2](z[2])
以此类推:
前向传播可以归纳为多次迭代z[l]=w[l]a[l-1]+b[l], a[l]=g[l](z[l])
向量化实现过程可以写成:Z[l]=W[l]a[l-1]+b[l], A[l]=g[l](Z[l]) (A[0]=X)
4.为什么使用深层表示(Why deep representations)

首先,深度网络究竟在计算什么?如果你在建一个人脸识别或是人脸检测系统,深度神经网络所做的事就是,当你宿儒一张脸部的照片,然后你可以把深度神经网络的第一层,当作一个特征探测器或者边缘探测器,在这个例子里,我们建立一个大概20个隐藏单元的深度神经网络,来解释是如何针对这张图计算的。隐藏单元就是这些图里这些小方块,举个例子,这个小方块就是一个隐藏单元,他会去找这张照片里“ l ”边缘的方向。那么这个隐藏单元(第四行第四列),可能是在找’‘—’‘水平向的边缘在哪里。我们可以先把神经网络的第一层看作图,然后去找这张照片的各个边缘。我们可以把照片里组成边缘的像素们放在一起看,然后它可以把被探测到的边缘组合合成面部的不同部分。比如说,可能有一个神经元会去找眼睛的部分,另外还有别的找鼻子的部分,然后把这些部分放在一起,比如眼睛鼻子下巴,就可以识别或是探测不同的人脸。
我们直觉上把这种神经网络的前几层当作探测简单的函数,比如边缘,之后把他们跟后几层结合起来,那么总体上就能学习更多复杂的函数。其实边缘探测器相对来说都是针对照片中非常小的面积,就像第一块,都是很小的区域。而面部探测器就会针对大一些的区域,但是主要的概念是:一般我们都会从比较小的细节入手,比如边缘,然后在一步步到更大更复杂的区域,比如一只眼睛或是一个鼻子,再把鼻子眼睛装一块组合成更加复杂的部分。
所以深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西。同时我们所计算的之前的几层,也就是相对简单的输入函数,比如图像的单元的边缘等等。到网络的深层的时候,我们实际上就可以做很多更加复杂的事,比如探测面部。
5.搭建神经网络块(Building blocks of deep neural networks)
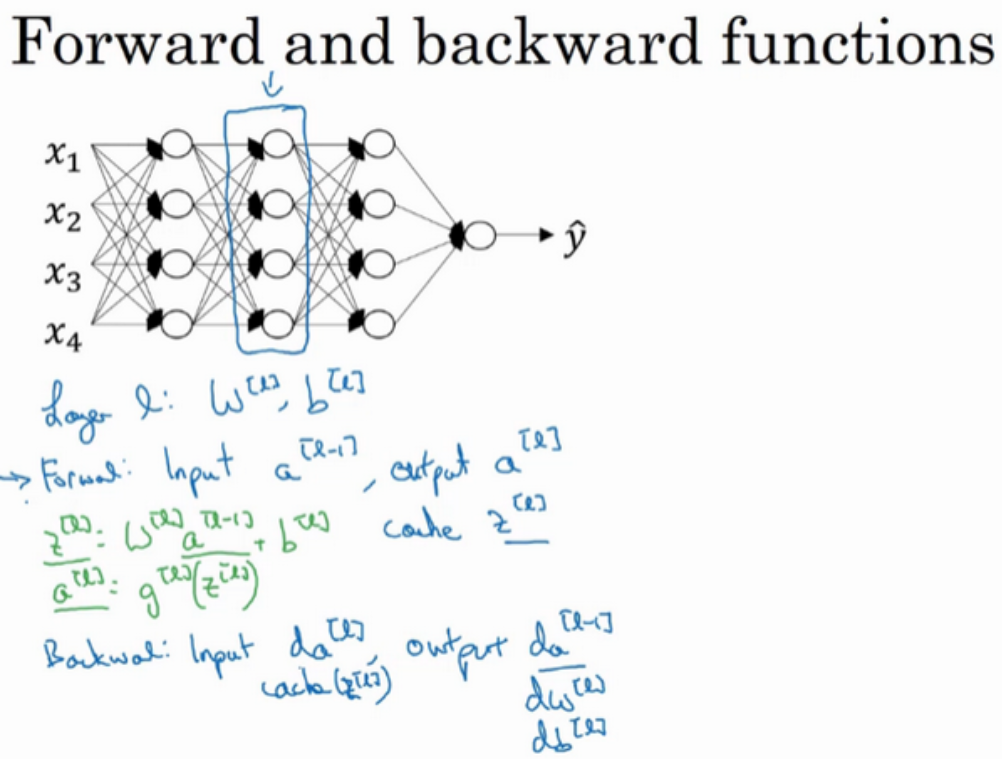
这是一个层数较少的神经网络,我们选择其中一层(方框部分),从这层的计算着手。在第l层有参数W[l]和b[l],正向传播里有输入的激活函数,输入是前一层a[l-1],输出是a[l],存在z[l]=W[l]a[l-1]+b[l],a[l]=g[l](z[l]),那么这就是如何从输入a[l-1]走到输出a[l],之后我们可以把z[l]的值缓存起来,原因在于z[i]对于以后的正向和反向传播步骤都非常重要。然后是反向传播步骤,同样也是第l层的计算,我们需要实现一个函数的输入为da[l],输出da[l-1]的函数。在这里我们需要注意,输入在这里其实是da[l]以及所缓存的z[l]的值,之前计算好的z[l]的值,处理输出da[l-1]以外,也需要输出需要的梯度dW[l]和db[l],这是为了实现梯度下降学习。
总结起来就是,在l层,我们会有正向函数,输入a[l-1]并且输出为a[l],为了计算结果你需要用到W[l]和b[l],以及输出到缓存的z[l]。然后用作反向传播的反向函数,数另外一个函数,输入da[l],输出da[l-1],此时我们会得到激活函数的导数,也就是希望的导数值da[l]。
之后如果我们实现了这两个正向和反向函数,那么神经网络的计算过程会是这样的:把输入特征a[0],放入到第一层并计算第一层的激活函数,用a[1]表示(需要用W[1]和b[1]来计算),之后我们同样缓存z[1]值,以此类推,到第二层,第三层,直到最后我们算出来a[L],第L层的最终输出值为y^。在这些过程中我们缓存了所有z的值,这就是正向传播的例子。
对于反向传播而言,我们需要一系列的反向迭代,具体如下图的流程图,就是这样反向计算梯度,需要把da[L]的值放在这里,,然后这个方块会计算出da[L-1]的值,以此类推,直到我们得到da[2]和da[1],其实还可以计算多一个输出值,就是da[0],但是这其实是你输入特征的导数,其值并不重要。在反向传播步骤中也会输出dW[i]和db[i]。目前为止我们算出了所有需要的导数。
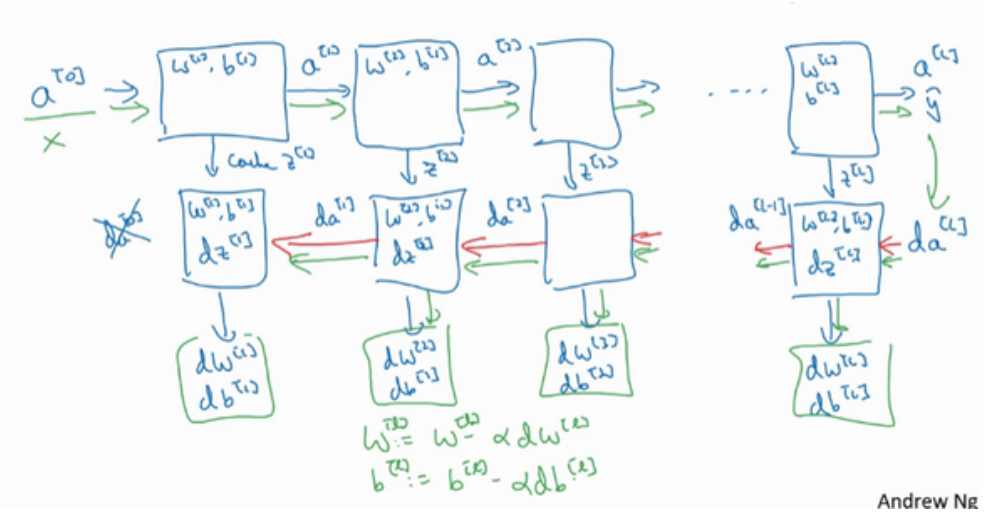
神经网络的一步训练包含了,从a[0]开始,也就是x然后经过一系列正向传播计算得到y^,之后再用输出值计算这个(第二行最后一个方块),再实现反向传播。现在,我们就有所有的导数项了,W也会在每层被更新为W=W-adW,b也是一样,b=b-adb ,反向传播就计算完毕,我们有所有的导数值,那么这是神经网络一个梯度下降循环。
6.参数VS超参数 (Parameters vs Hyperparameters)
想要你的神经网络起到很好的作用,我们必须规划好参数和超参数。那么,什么十超参数?比如算法中的learning rate a(学习率)、iterations(梯度下降法循环的数量)、L(隐藏层数目)、n[l](隐藏层单元数目)、choice of activation funcction(激活函数的选择)都需要我们来设置,这些数字实际上控制了最后参数W和b 的值,所以他们被称为超参数。
那么,如何寻找超参数的最优值?
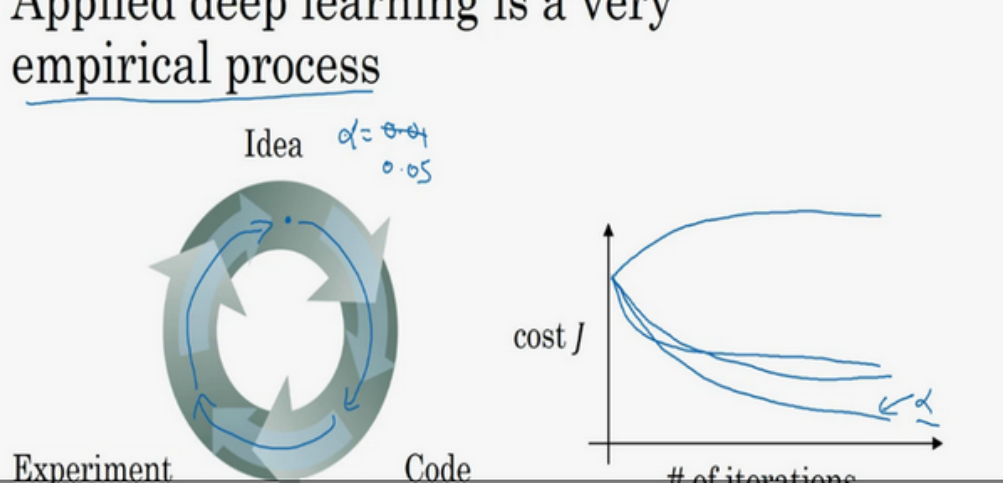
我想Idea——Code——Experiment——Idea这个循环,尝试各种不同的参数,实现模型并且观察是否成功,然后再迭代。实际上,今天的深度学习应用领域,对于最优超参数的值还只是一个经验性的过程。当我们在开发新应用的啥时候,预先很难知道,究竟超参数的最优值应该是数目,所以通常,我们必须尝试很多不同的值,并走这个循环,尝试各种参数。
7.深度学习和大脑的关联性(What does this have to do with the brain?)
为什么人们会说深度学习和大脑相关呢?
当你在实现一个神经网络的时候,那些公式是你在做的东西,你会做前向传播,反向传播,梯度下降法,其实很难表达这些公式具体做了什么,深度学习像大脑这样的类比其实过度简化了我们大脑具体在做什么,但因为这种形式很简洁,也很能让普通人更愿意公开讨论,也方便新闻报道,但其实这个类比是非常不正确的。
一个神经网络的逻辑单元可以看成是对一个生物神经元的过度简化,但是迄今为止连神经科学家都很难解释究竟一个神经元能做什么,它是极其复杂的;它的一些功能可能真的类似logistic 回归的运算,但单个神经元到底在做什么目前还没有人可以真正解释。
深度学习确实是一个很好的工具来学习各种很灵活很复杂的函数,学习到从x到y 的映射,在监督学习中学到从输入到输出的映射。但是这种和人类大脑的类比,在这个领域的早期也许值得一提,但现在这个类比已经过时了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号