如何理解动态规划？

https://www.zhihu.com/question/39948290/answer/883302989

本人掌握动态规划的过程，有点钻牛角尖，这里用我的心历路程给各位同学们做个提醒。

long time ago, 当我刚看到动态规划这个响亮的大名时，瞬间陷入了沉思，脑中浮想联翩，揣摩着这个算法应该很带感。

查了一下维基百科（不建议你阅读）

动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被储存，从简单的问题直到整个问题都被解决。因此，动态规划储存递迴时的结果，因而不会在解决同样的问题时花费时间。
动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

看了上面这一段之后，我完全懵逼了。

然后找了一个入门动态规划的简单例子（斐波那契数列），看懂后，再看看这四个响亮的大字"动态规划"，我更加混乱了。

当查了许多资料，确认自己最终理解后，再看这四个大字"动态规划"，我。。。。

说好的动态呢？这明明是高中数列题的魔改版好吗？这是谁取的名字，我真看不出这算法哪里动态了！这望文生义害人不浅啊。如果我来命名，可能会取：分步规划，分步存储法， 递推存储法，数列递推法，状态转移法.....但我就是想不出动态规划啊。

所以，入门动态规划第一条：切忌望文生义，切忌用名字反推算法！

不过，还真有人对动态规划的名字进行了介绍，有兴趣可以参考外国版知乎quora回答

废话不多说，进入正题！

---

能用动态规划解决的问题

如果一个问题满足以下两点，那么它就能用动态规划解决。

1. 问题的答案依赖于问题的规模​，也就是问题的所有答案构成了一个数列。举个简单的例子，1个人有2条腿，2个人有4条腿，...，​  个人有多少条腿？答案是​  条腿。这里的​  是问题的答案，​  则是问题的规模，显然问题的答案是依赖于问题的规模的。答案是因变量，问题规模是自变量。因此，问题在所有规模下的答案可以构成一个数列​  ，比如刚刚“数腿”的例子就构成了间隔为2的等差数列  ​。
2. 大规模问题的答案可以由小规模问题的答案递推得到，也就是​的值可以由​中的个别求得。还是刚刚“数腿”的例子，显然  ​可以基于  ​求得：​  。

---

适合用动态规划解决的问题

能用动态规划解决，不代表适合用。比如刚刚的“数腿”例子，你可以写成​  的显式表达式形式，那么杀鸡就不必用牛刀了。但是，在许多场景，​  的显式式子是不易得到的，大多数情况下甚至无法得到，动态规划的魅力就出来了。

---

应用动态规划——将动态规划拆分成三个子目标

当要应用动态规划来解决问题时，归根结底就是想办法完成以下三个关键目标。

1. 建立状态转移方程
   这一步是最难的，大部分人都被卡在这里。这一步没太多的规律可说，只需抓住一个思维：当做已经知道​~​的值，然后想办法利用它们求得​。在“数腿”的例子中，状态转移方程即为​  。
2. 缓存并复用以往结果
   这一步不难，但是很重要。如果没有合适地处理，很有可能就是指数和线性时间复杂度的区别。假设在“数腿”的例子中，我们不能用显式方程，只能用状态转移方程来解。如果现在  ​未知，但是刚刚求解过一次  ​。如果不将其缓存起来，那么求  ​时，我们就必须花100次加法运算重新获取。但是如果刚刚缓存过，只需复用这个子结果，那么将只需一次加法运算即可。
3. 按顺序从小往大算
   这里的“小”和“大”对应的是问题的规模，在这里也就是我们要从  ​,  ​, ... 到​  依次顺序计算。这一点在“数腿”的例子来看，似乎显而易见，因为状态方程基本限制了你只能从小到大一步步递推出最终的结果（假设我们仍然不能用显式方程）。然而当问题复杂起来的时候，你有可能乱了套，所以必须记住这也是目标之一。

---

高中数列题的魔改版

看到这里，你可能会觉得怎么跟高中的数列题那么像？？其实在我看来这就是高中数列题的魔改版。

高中的题一般需先推导出状态转移方程（在高中时代称为通项公式），再据此推导出显式表达式。然而，动态规划是要我们在推导出状态转移方程后，根据状态转移方程用计算机暴力求解出来。显式表达式？在动态规划中是不存在的！

就是因为要暴力计算，所以前面说的目标有两个是涉及到代码层面上：

• 缓存中间结果：也就是搞个数组之类的变量记录中间结果。
• 按顺序从小往大算：也就是搞个for循环依次计算。

---

例子

古语有云：talk is cheap，show me the code。接下来用3个例子印证上面的思想，例子均用python3（不懂没关系看备注）。例子是从简单，困难到地狱级别的题目。

 

斐波那契数列（简单）

斐波那契数列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……
它遵循这样的规律：当前值为前两个值的和。
那么第  ​个值为多少？

首先，我们可以很容易得到状态转移方程：​  。接下来我们用两种方法来做：

 

1. 简单递归(反例)

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)
    
if __name__ == '__main__':
    result = fib(100)  # 你等到天荒地老，它还没有执行完

如上所示，代码简单易懂，然而这代码却极其低效。先不说这种递归的方式造成栈空间的极大浪费，就仅仅是该算法的时间复杂度已经属于​  了。指数级别时间复杂度的算法跟不能用没啥区别！

为什么是指数时间复杂度？图1通过展示求解  ​的过程说明了其原因。如图，随着递归的深入，计算任务不断地翻倍！

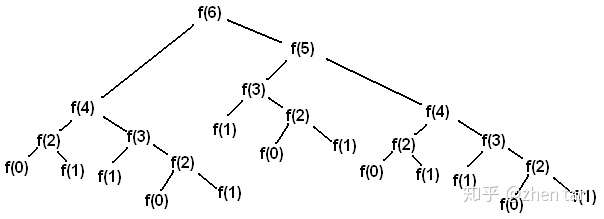图1 简单递归的执行过程

2. 动态规划

def fib(n):
    
    results = list(range(n+1)) # 用于缓存以往结果，以便复用（目标2）
    
    for i in range(n+1):  # 按顺序从小往大算（目标3）
        if i < 2:
            results[i] = i
        else:
            # 使用状态转移方程（目标1），同时复用以往结果（目标2）
            results[i] = results[i-1] + results[i-2] 
     
    return results[-1]
​
    
    
if __name__ == '__main__':
    result = fib(100)  # 秒算，result为：354224848179261915075

如上代码，针对动态规划的三个子目标，都很好地实现了（参考备注），具体为：

• 目标1，建立状态转移方程（完成）。也就是前面的  ​。
• 目标2，缓存并复用以往结果（完成）。图1的简单递归存在大量的重复任务。在线性规划解法中，我们把结果缓存在results列表，同时在results[i] = results[i-1] + results[i-2]中进行了复用。这相当于我们只需完成图2中红色部分的计算任务即可，时间复杂度瞬间降为  ​。

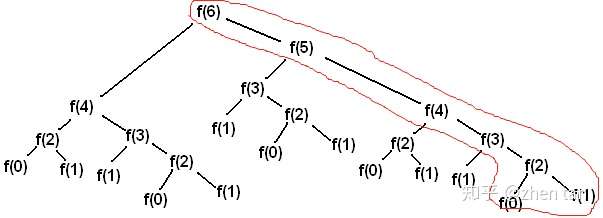图2 线性规划通过缓存与复用机制将计算规模缩小到红色部分*

• 目标3，按顺序从小往大算（完成）。for循环实现了从0到​  的顺序求解，让问题按着从小规模往大规模求解的顺序走。

 

不同路径（困难）

本题来源于LeetCode，官网上用了一些例子进行了解释，请点击查看具体详情不同路径。题目如下：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？

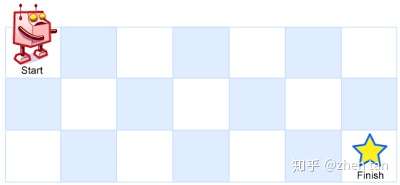
例如，上图是一个7 x 3 的网格。有多少可能的路径？

先自己思考1min……再看答案

解这题，如前所述，我们需要完成三个子目标

1. 建立状态转移方程。该题就难在这里，这一步搞不定基本上GG了。实际上，如图3所示，第​  行第  ​列的格子的路径数，是等于它左边格子和上面格子的路径数之和：  ​。

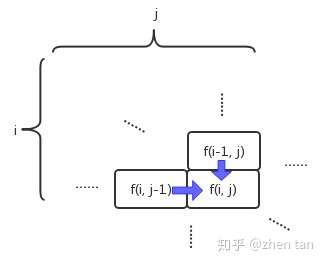​图3 状态转移方程推导图解

2. 缓存并复用以往结果。与之前说的一维数列不同，这里的中间结果可以构成一个二维数列（如图3），所以需要用二维的数组或者列表来存储。

3. 按顺序从小往大算。这次有两个维度，所以需两个循环，分别逐行和逐列让问题从小规模到大规模计算。

以下是具体代码

# m是行数，n是列数
def count_paths(m, n):    
    
    results = [[1] * n] * m  # 将二维列表初始化为1，以便之后用于缓存（目标2）
    # 题外话：results的空间复杂度不是O(nm)，是O(n)
    
    # 第0行和第0列的格子路径数显然均取值为1，所以跳过
    for i in range(1, m):       # 外循环逐行计算（目标3）
        for j in range(1, n):   # 内循环逐列计算（目标3）    
            # 状态方程（目标1），以及中间结果复用（目标2）
            results[i][j] = results[i-1][j] + results[i][j-1]  
            
    return results[-1][-1]


if __name__ == '__main__':
    result = count_paths(7, 3) # 结果为28  

 

正则表达式匹配（地狱）

本题来源于LeetCode，我把题目进行了简化，以便突出重点。更具体的说明可以参考官网正则表达式。题目如下：

给你一个字符串 string 和一个字符规律 pattern，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

可以先自己思考3min……再看答案。

老样子，我们需要完成三个子目标

1. 建立状态转移方程。这里的状态转移方程有些复杂，我折腾了一段时间才总结出来的，如果看不懂就跳过不用纠结，毕竟文章的重点不在此。

• 首先我们进行如下定义:

​  ： pattern的第0~​  个字符与string的第0~  ​个字符的匹配结果。结果只取True（匹配成功），或者False（匹配失败）。
 ​：pattern的第​  个字符。
 ​：string的第  ​个字符。
​  ：单个字符  ​和  ​的匹配结果。结果只取True（匹配成功），或者False（匹配失败）。

• 那么参考如图4，可得下面的状态转移方程。具体地说有两种情况（看不懂这里就跳过吧，篇幅有限不能大书特书）：

(1). 如果  ​为星号外的任意字符，用“x”表示。这种情况显而易见，​  是基于  ​的结果（可能成功或者失败的）继续配对。

(2). 如果  ​为星号“*”。如图4右边，分三种子情况。箭头1描述了  ​匹配成功了0次的情况，所以继承前面匹配的结果  ；箭头2描述了  ​成功匹配了1次的情况，所以继承这1次的结果  ；箭头3表示  ​成功匹配超过1次，所以基于左边的结果继续匹配  。

其中

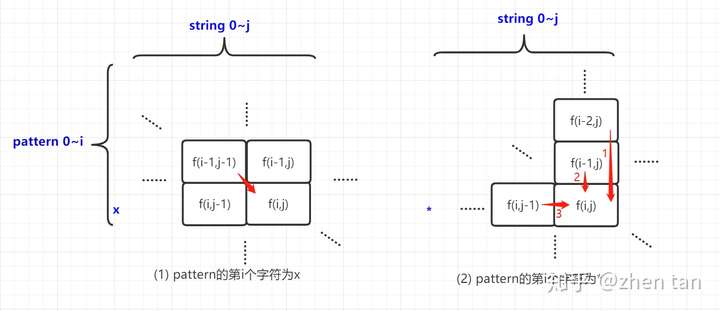​图4 状态转移方程的4种情况

2. 缓存并复用以往结果。如图4仍然用二维数组，存的是布尔型。

3. 按顺序从小往大算。参考代码。

代码实现如下，里面提到的哨兵是用于处理临界问题的，自己跑跑代码就懂了：

​
# 状态转移函数（目标1）
def f(pattern, i, string, j, results):
    # 当前是星号
    if pattern[i] == '*':
        m_ij = pattern[i - 1] == string[j] or pattern[i - 1] == '.'
        r = results[i - 2][j] | results[i - 1][j] | results[i][j - 1] & m_ij

    # 当前不是星号
    else:
        m_ij = pattern[i] == string[j] or pattern[i] == '.'
        r = results[i - 1][j - 1] & m_ij

    return r


# 主匹配函数
def is_match(string, pattern):

    # 初始化二维数组（目标2）
    len_string = len(string) + 1  # 给二维数组加哨兵，所以+1
    len_pattern = len(pattern) + 1
    results = [[False] * len_string for i in range(len_pattern)]
    results[0][0] = True
    pattern = '_' + pattern  # 兼容哨兵
    string = '_' + string

    # 异常处理
    if len_pattern == len_string == 1:
        return True
    if len_pattern == 1:
        return False
    if pattern[0] == '*':
        return False

    # 外循环遍历pattern（目标3）
    for i in range(1, len_pattern):

        # 这里是哨兵处理相关（与星号的情况1相关）
        if pattern[i] == '*':
            results[i][0] = results[i - 2][0]

        # 内循环遍历string（目标3）
        for j in range(1, len_string):
            # 状态转移函数（目标1），以及复用中间结果（目标2）
            results[i][j] = f(pattern, i, string, j, results)


    return results[-1][-1]



if __name__ == '__main__':
    string = "aab"
    pattern = "c*a*b"
    result = is_match(string, pattern) # 结果为true

 

以上三个例子的空间复杂度是可以进一步优化的，这与动态规划的思想关系不大，不做细说，读者自己思考完成。

 

---

总结

动态规划与其说是一个算法，不如说是一种方法论。该方法论主要致力于将合适的问题拆分成三个子目标一一击破：

1. 建立状态转移方程
2. 缓存并复用以往结果
3. 按顺序从小往大算

完成该三个目标，你将所向披靡。

以上是一家之言，如有谬误，欢迎指出。