B树、B+树
引言
最近在复习数据库索引相关的知识,B+树是数据库索引中十分重要的数据结构。
学习过程中,发现对B树和B+树之类的数据结构知识很欠缺,一起来回顾一下。
学习
索引
如果没有索引,我们想从数据库中查询数据,需要遍历整个表。
如果表中的数据量小时还好,如果表中数据量很大,这就很耗时了。

这就类似我们有一个字不认识了,然后去查字典。
我们想要在字典中快速查询出这个字,需要根据偏旁部首去一步步定位这个字的位置。
数据库中也是类似这么查询的,根据已知的条件,一步步去定位数据所在的位置,从而避免遍历整张表,提高查询效率,这就是索引。
假设让我们去设计索引的存储结构,我们会怎么设计呢?
平衡二叉树
这是我们最熟悉的数据结构了,十分简单。
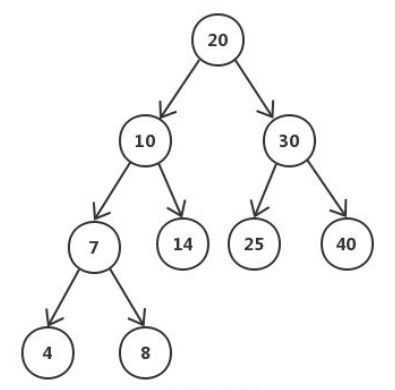
左右子树的深度差不超过一,根节点的左子树上的节点都比它小,根节点的右子树的节点都比它大,它的左右子树也都是平衡二叉树。、
如果使用平衡二叉树来设计索引,避免了遍历整张表,最坏的情况,是O(logN)的时间复杂度。即这棵树的高度。
当数据量很大时,O(logN)并不能满足我们的需要,所以我们需要其他高度更低的树。
B树
我们总能看到有B-树这个名词,我之前一直叫B减树,暴露了没文化的缺陷。
这个-不是减号,是分隔符,B-树就是B树。
B树为了让树的高度更低,在一个树节点中包含多条数据,并包含多个指针
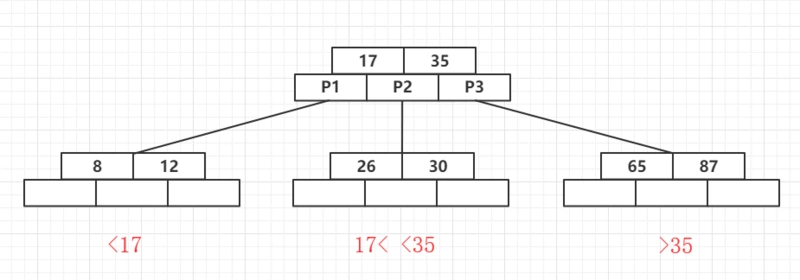
查询小于17的,去找P1的子树。
查询大于17小于35的,去找P2的子树。
查询大于35的,去找P3的子树。
因为叉多了,所以高度就低,复杂度就低。
B+树
B树已经足够优秀了,它的查询复杂度足够低,可以满足数据库索引的需求了,随着科技的进步,衍生出了一种更加优秀的数据结构——B+树。
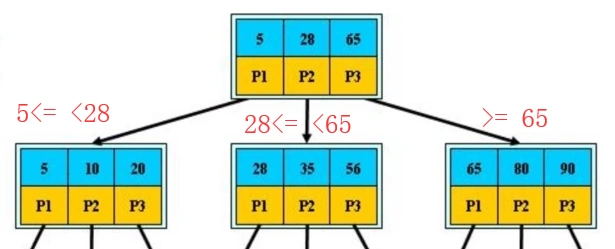
我们先来看最上面的三个指针。
查询大于等于5,并且小于28的,去找P1的子树。
查询大于等于28,并且小于65的,去找P2的子树。
查询大于等于65的,去找P3的子树。直到查找到叶子节点。
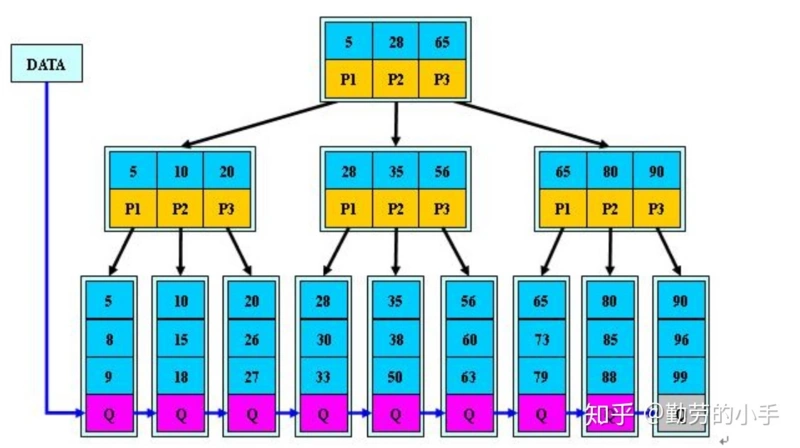
与B树不同的是,B+树的所有数据都是存在于叶子节点中。在树中去寻找5,也是需要遍历到叶子节点。
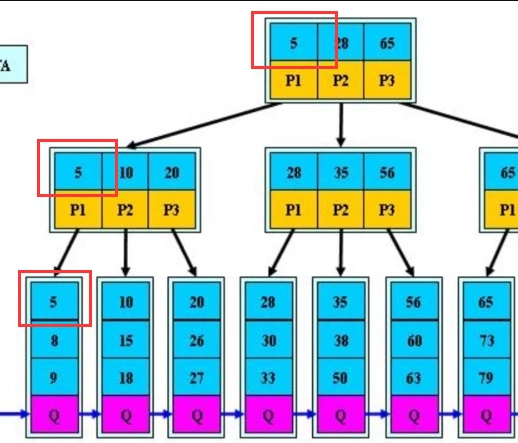
这样设计就带来了两个优点:
B+树的非叶子节点没有存储数据指针,减少了节点占用的空间,可以减少IO的次数。- 同时,因为所有数据都存在叶子节点上,所以对于每条数据来说,查询的复杂度是相同的,查询效率更稳定。
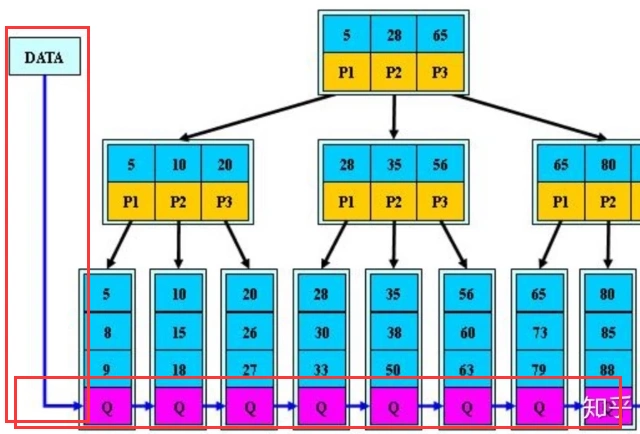
同时,所有叶子节点本身根据关键字的大小进行连接,从而可以十分快速地实现范围查询。
因为诸多优点,数据库主流索引都采用B+树来实现。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号