排序算法整理(啊哈算法)
一、桶排序
这是一个非常快的排序算法。桶排序从1956年就开始被使用,该算法的基本思想是由
E.J.Issac 和R.C.Singleton 提出来的。之前我说过,其实这并不是真正的桶排序算法,真正的
桶排序算法要比这个更加复杂。
示例:数组 {5, 3, 5, 2, 8} 进行排序(已知最大数值不会超过 10)
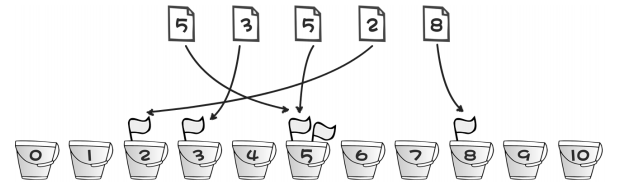
代码如下:

总结:排序很快,但是性能损耗很大,对未知大小的数组无法使用,同时浮点型的排序难度非常大。
二、经典排序冒泡
冒泡排序的基本思想是:每次比较两个相邻的元素,如果它们的顺序错误就把它们交换 过来。
代码如下:

总结:经典排序算法,两个 for 循环,临时变量更换数组位置从而达到排序目的;
三、快速排序
冒泡排序可以说是我们学习的第一个真正的排序算法,并且解决了桶排序浪费 空间的问题,
但在算法的执行效率上却牺牲了很多,它的时间复杂度达到了O(N ²) 。
假如我 们的计算机每秒钟可以运行10亿次,那么对 1 亿个数进行排序,桶排序只需要 0.1秒,
而冒 泡排序则需要1 千万秒,达到 115 天之久,是不是很吓人?
那有没有既不浪费空间又可以快 一点的排序算法呢?那就是“快速排序”啦!光听这个名字是不是就觉得很高端呢?
示例:数组 {6, 1, 2, 7, 9, 3, 4, 5, 10, 8}
思路: 两端开始“探测”。先从 右往左找一个小于6 的数,再从左往右找一个大于6 的数,然后交换它们。
这里可以用两个 变量 i 和 j ,分别指向序列最左边和最右边。
我们为这两个变量起个好听的名字“哨兵 i ”和 “哨兵j”。
刚开始的时候让哨兵 i 指向序列的最左边(即 i =1),指向数字 6。让哨兵 j 指向序列的最右边(即j =10 ),指向数字 8 。
如图解:

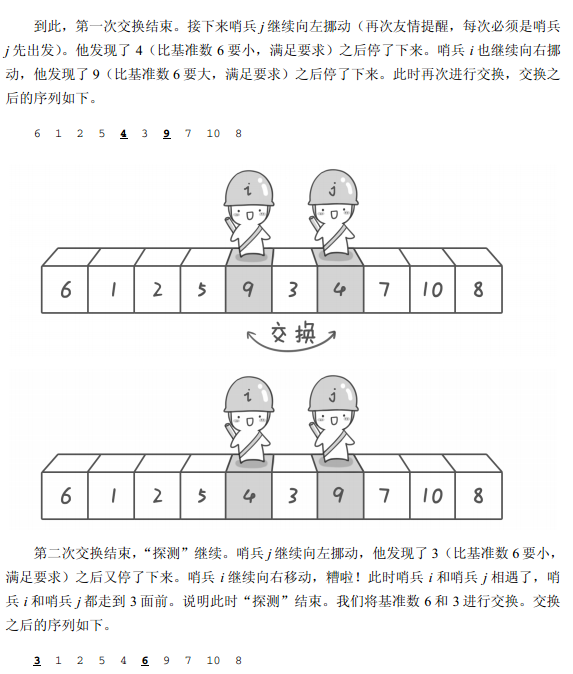



示例代码:
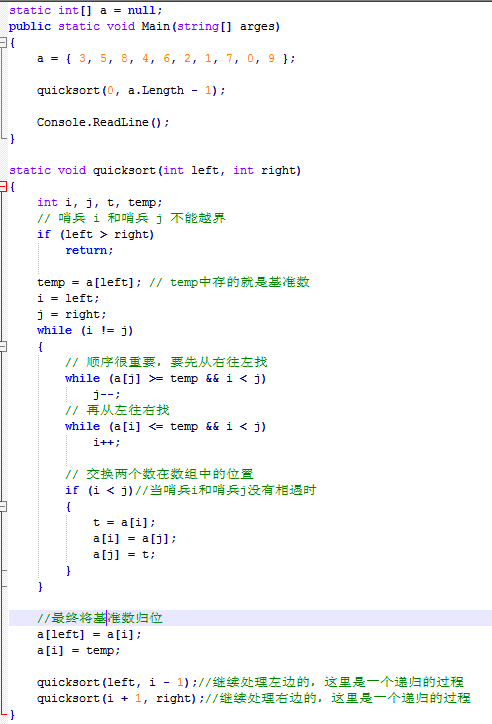
总结:其实快速排序是基于一 种叫做“二分”的思想。
注解:
快速排序之所以比较快,是因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候
设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全
部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样只能在相邻的数之间进
行交换,交换的距离就大得多了。因此总的比较和交换次数就少了,速度自然就提高了。当
然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和
冒泡排序是一样的,都是 O(N²),它的平均时间复杂度为 O ( N logN )。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号