树和二叉树知识整理
大学的课程 数据结构 工作中得时不时翻翻,要不然容易忘,这里简单整理下知识点。
一、树的定义
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。
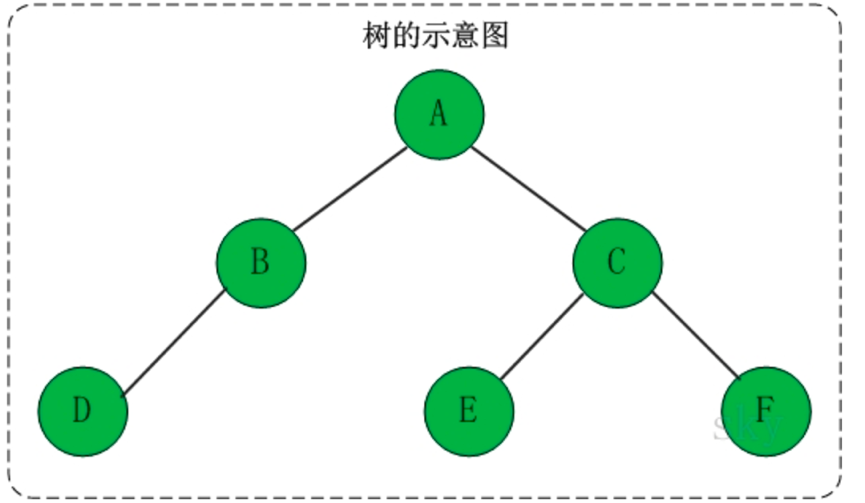
树具有的特点有:
(1)每个结点有零个或多个子结点
(2)没有父节点的结点称为根节点
(3)每一个非根结点有且只有一个父节点
(4)除了根结点外,每个子结点可以分为多个不相交的子树。
树的基本术语有:
若一个结点有子树,那么该结点称为子树根的“双亲”,子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 树的度:一棵树中,最大的节点的度称为树的度;
- 叶节点或终端节点:度为零的节点;
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙;
- 森林:由m(m>=0)棵互不相交的树的集合称为森林。
表格说话:
| Root | The top node in a tree. | 根 | 树的顶端结点 |
| Child | A node directly connected to another node when moving away from the Root. | 孩子 | 当远离根(Root)的时候,直接连接到另外一个结点的结点被称之为孩子(Child); |
| Parent | The converse notion of a child. | 双亲 | 相应地,另外一个结点称为孩子(child)的双亲(parent)。 |
| Siblings | A group of nodes with the same parent. | 兄弟 | 具有同一个双亲(Parent)的孩子(Child)之间互称为兄弟(Sibling)。 |
| Ancestor | A node reachable by repeated proceeding from child to parent. | 祖先 | 结点的祖先(Ancestor)是从根(Root)到该结点所经分支(Branch)上的所有结点。 |
| Descendant | A node reachable by repeated proceeding from parent to child. | 子孙 | 以某结点为根的子树中的任一结点都称为该结点的子孙(后代)。 |
| Leaf | A node with no children. | 叶子(终端结点) | 没有孩子的结点(也就是度为0的结点)称为叶子(Leaf)或终端结点。 |
| Branch | A node with at least one child. | 分支(非终端结点) | 至少有一个孩子的结点称为分支(Branch)或非终端结点。 |
| Degree | The number of sub trees of a node. | 度 | 结点所拥有的子树个数称为结点的度(Degree)。 |
| Edge | The connection between one node and another. | 边 | 一个结点和另一个结点之间的连接被称之为边(Edge)。 |
| Path | A sequence of nodes and edges connecting a node with a descendant. | 路径 | 连接结点和其后代的结点之间的(结点,边)的序列。 |
| Level | The level of a node is defined by 0 + (the number of connections between the node and the root). | 层次 | 结点的层次(Level)从根(Root)开始定义起,根为第0层,根的孩子为第1层。以此类推,若某结点在第i层,那么其子树的根就在第i+1层。 |
| Height of node | The height of a node is the number of edges on the longest path between that node and a leaf. | 结点的高度 | 结点的高度是该结点和某个叶子之间存在的最长路径上的边的个数。 |
| Height of tree | The height of a tree is the height of its root node. | 树的高度 | 树的高度是其根结点的高度。 |
| Depth of node |
The depth of a node is the number of edges from the tree's root node to the node. | 结点的深度 | 结点的深度是从树的根结点到该结点的边的个数。 (注:树的深度指的是树中结点的最大层次。) |
| Forest | A forest is a set of n ≥ 0 disjoint trees. | 森林 | 森林是n(>=0)棵互不相交的树的集合。 |
树的种类:
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
- 二叉树:每个节点最多含有两个子树的树称为二叉树;
- 完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树,其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
- 平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
- 排序二叉树(二叉查找树(英语:Binary Search Tree),也称二叉搜索树、有序二叉树);
- 霍夫曼树(用于信息编码):带权路径最短的二叉树称为哈夫曼树或最优二叉树;
- B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树
二、二叉树
1、二叉树的定义
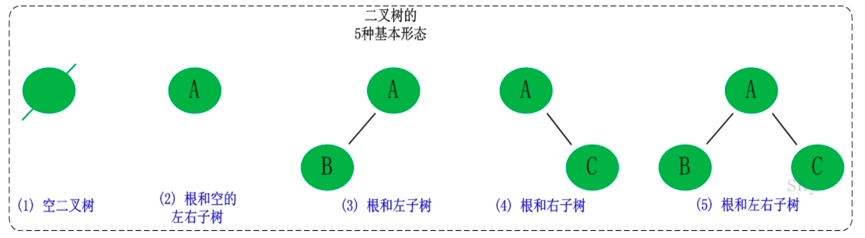
二叉树是每个结点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
2、二叉树的性质
性质1:二叉树第i层上的结点数目最多为2i-1(i>=1)
性质2:深度为k的二叉树至多有2k-1个结点(k>=1)
性质3:包含n个结点的二叉树的高度至少为(log2n)+1
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
3、性质4的证明
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:因为二叉树中所有结点的度数均不大于2,不妨设n0表示度为0的结点个数,n1表示度为1的结点个数,n2表示度为2的结点个数。三类结点加起来为总结点个数,于是便可得到:n=n0+n1+n2 (1)
由度之间的关系可得第二个等式:n=n0*0+n1*1+n2*2+1即n=n1+2n2+1 (2)
将(1)(2)组合在一起可得到n0=n2+1
4、二叉树的遍历(要有递归的思想!)
(1):先序遍历:根->左子树->右子树(先序)
(2):中序遍历:左子树->根->右子树(中序)
(3):后序遍历:左子树->右子树->根(后序)
这三种遍历方法只是访问结点的时机不同,访问结点的路径都是一样的,时间和空间复杂度皆为O(n)。
5、二叉树存储方式
二叉树是非线性结构,即每个数据结点至多只有一个前驱,但可以有多个后继。它可采用顺序存储结构和链式存储结构。
即有链表和数组两种,用数组存访问速度快,但插入、删除节点操作就比较费时了。实际中更多的是用链来表示二叉树的。
顺序存储(只适用于完全二叉树)——可以用于排序算法中的堆排序
链式存储(最普遍的存储方式)——由于结点可能为空,所以会比较浪费空间
三、满二叉树、完全二叉树和二叉查找树
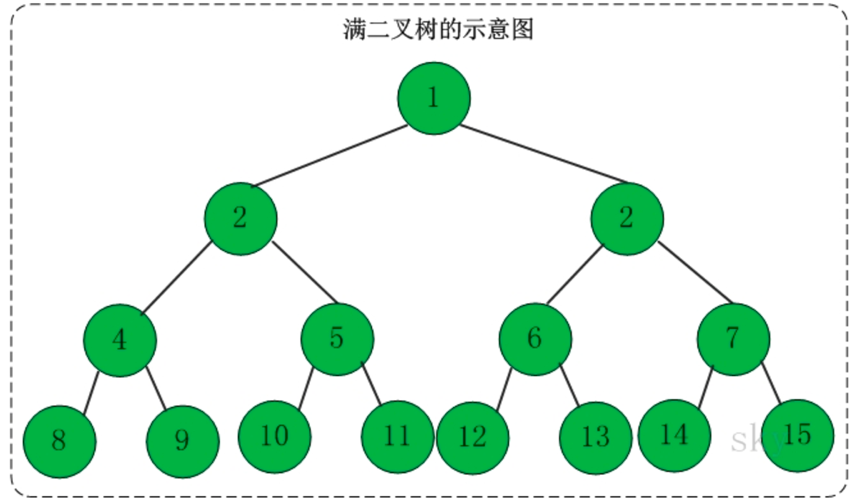
1、满二叉树
定义:高度为h,并且由2h-1个结点组成的二叉树,称为满二叉树
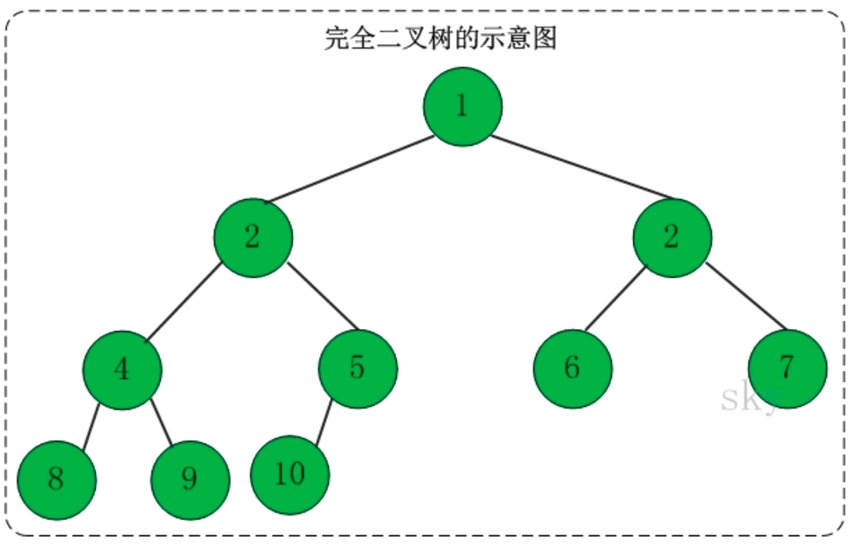
2、完全二叉树
定义:一棵二叉树中,只有最下面两层结点的度可以小于2,并且最下层的叶结点集中在靠左的若干位置上,这样的二叉树称为完全二叉树。
特点:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。显然,一棵满二叉树必定是一棵完全二叉树,而完全二叉树未必是满二叉树。
面试题:如果一个完全二叉树的结点总数为768个,求叶子结点的个数。
由二叉树的性质知:n0=n2+1,将之带入768=n0+n1+n2中得:768=n1+2n2+1,因为完全二叉树度为1的结点个数要么为0,要么为1,那么就把n1=0或者1都代入公式中,很容易发现n1=1才符合条件。所以算出来n2=383,所以叶子结点个数n0=n2+1=384。
总结规律:如果一棵完全二叉树的结点总数为n,那么叶子结点等于n/2(当n为偶数时)或者(n+1)/2(当n为奇数时)
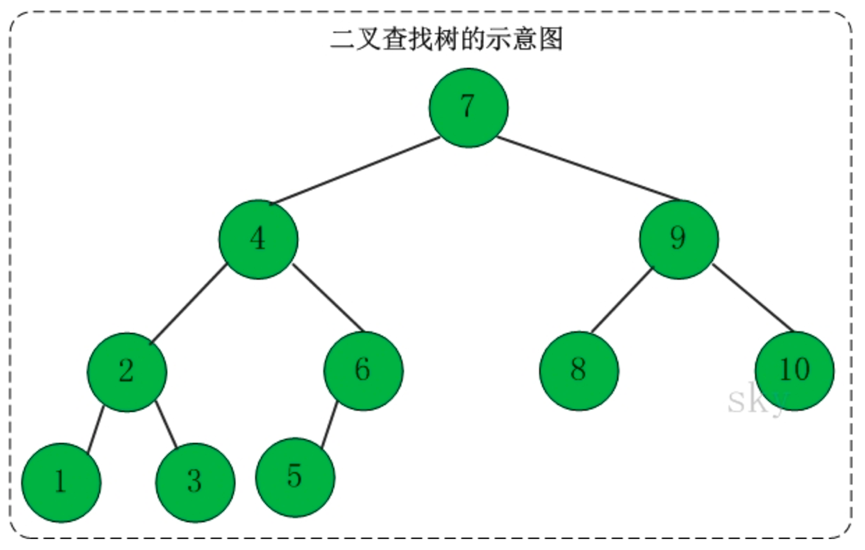
3、二叉查找树
定义:二叉查找树又被称为二叉搜索树。设x为二叉查找树中的一个结点,x结点包含关键字key,结点x的key值计为key[x]。如果y是x的左子树中的一个结点,则key[y]<=key[x];如果y是x的右子树的一个结点,则key[y]>=key[x]
在二叉查找树中:
(1)若任意结点的左子树不空,则左子树上所有结点的值均小于它的根结点的值。
(2)任意结点的右子树不空,则右子树上所有结点的值均大于它的根结点的值。
(3)任意结点的左、右子树也分别为二叉查找树。
(4)没有键值相等的结点。
四、平衡二叉树及其它树
1、平衡二叉树
平衡二叉树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列,可以参考Fibonacci(斐波那契)数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。
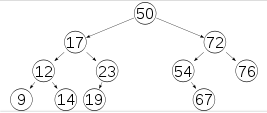
对于平衡二叉树要特别注意的是,不要求非叶节点都有两个子结点,仅要求两个子树的高度差的绝对值不超过1,或者为空树。
平衡二叉树特点:①非叶子节点最多拥有两个子节点。②非叶子节点值大于左边子节点、小于右边子节点。③树的左右两边的层级数相差不会大于1。④没有值相等重复的节点。
2、B树(B-tree)
注意:之前有看到有很多文章把B树和B-tree理解成了两种不同类别的树,其实这两个是同一种树。
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),数据库索引技术里大量使用者B树和B+树的数据结构。让我们来看看他有什么特点
(1)排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则;
(2)子节点数:非叶节点的子节点数>1,且<=M ,且M>=2,空树除外(注:M阶代表一个树节点最多有多少个查找路径,M=M路,当M=2则是2叉树,M=3则是3叉);
(3)关键字数:枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2);
(4)所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子;
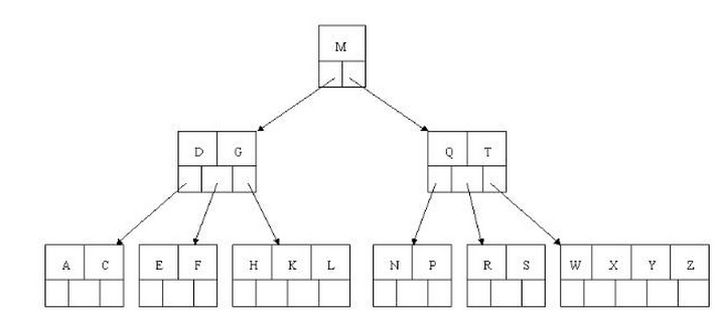
B树的查询流程:
如上图我要从上图中找到E字母,查找流程如下
(1)获取根节点的关键字进行比较,当前根节点关键字为M,E<M(26个字母顺序),所以往找到指向左边的子节点(二分法规则,左小右大,左边放小于当前节点值的子节点、右边放大于当前节点值的子节点);
(2)拿到关键字D和G,D<E<G 所以直接找到D和G中间的节点;
(3)拿到E和F,因为E=E 所以直接返回关键字和指针信息(如果树结构里面没有包含所要查找的节点则返回null);
B树的插入节点流程:
定义一个5阶树(平衡5路查找树;),现在我们要把3、8、31、11、23、29、50、28 这些数字构建出一个5阶树出来;
遵循规则:
(1)节点拆分规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须<=5-1(这里关键字数>4就要进行节点拆分);
(2)排序规则:满足节点本身比左边节点大,比右边节点小的排序规则;
先插入 3、8、31、11
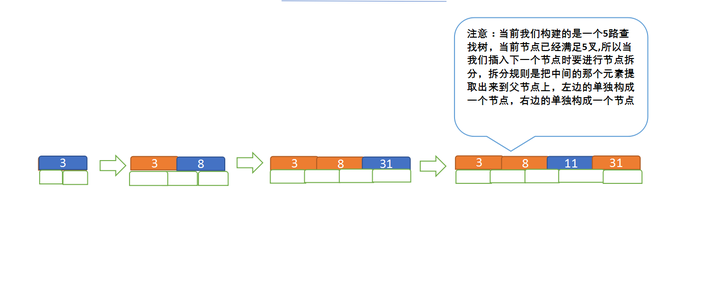
再插入23、29
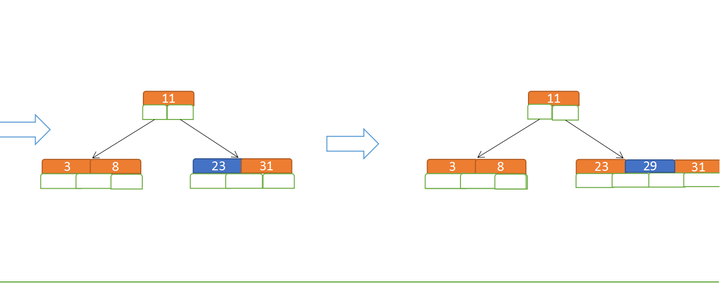
再插入50、28
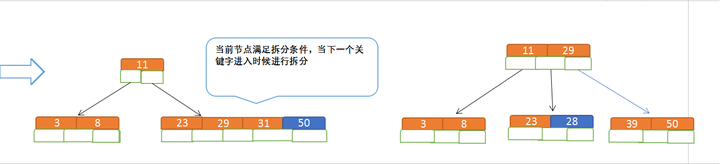
B树节点的删除:
规则:
(1)节点合并规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须大于等于ceil(5/2)(这里关键字数<2就要进行节点合并);
(2)满足节点本身比左边节点大,比右边节点小的排序规则;
(3)关键字数小于二时先从子节点取,子节点没有符合条件时就向向父节点取,取中间值往父节点放;
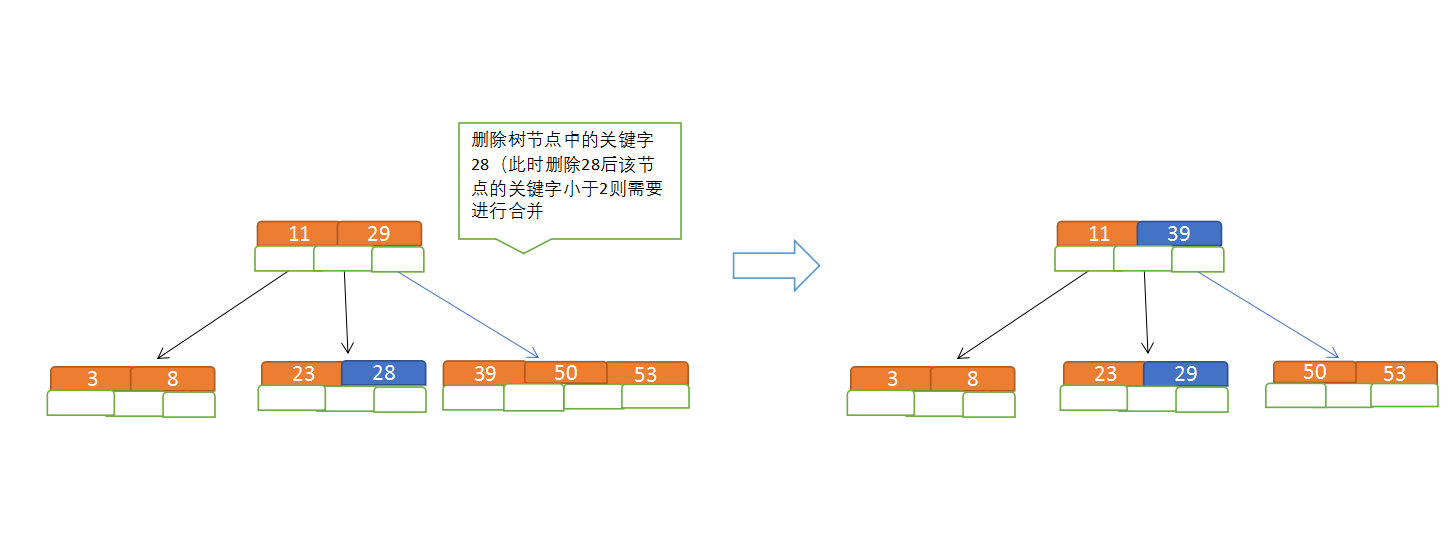
特点:
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库中的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘快大小范围;把树的节点关键字增多后树的层级比原来的二叉树少了,减少数据查找的次数和复杂度;
3、B+树
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别
(1)B+跟B树不同B+树的非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得B+树每个非叶子节点所能保存的关键字大大增加;
(2)B+树叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样;
(3)B+树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
(4)非叶子节点的子节点数=关键字数(来源百度百科)(根据各种资料 这里有两种算法的实现方式,另一种为非叶节点的关键字数=子节点数-1(来源维基百科),虽然他们数据排列结构不一样,但其原理还是一样的Mysql 的B+树是用第一种方式实现);
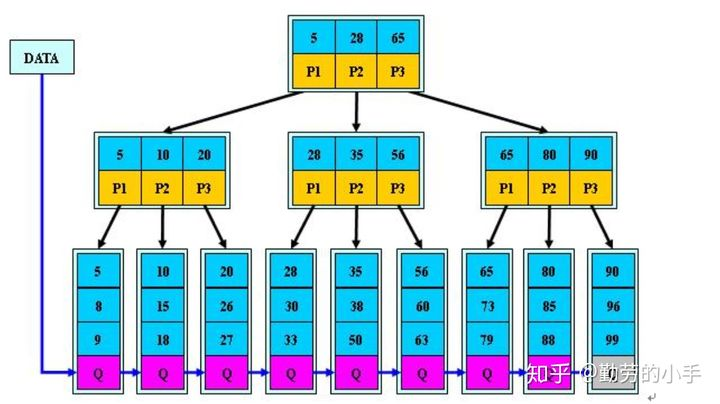
特点:
1、B+树的层级更少:相较于B树B+每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快;
2、B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比B树更稳定;
3、B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
4、B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
B树相对于B+树的优点是,如果经常访问的数据离根节点很近,而B树的非叶子节点本身存有关键字其数据的地址,所以这种数据检索的时候会要比B+树快。
4、红黑树
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意:
(01) 特性(3)中的叶子节点,是只为空(NIL或null)的节点。
(02) 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
红黑树示意图如下:
5、哈夫曼树
哈夫曼树(霍夫曼树)又称为最优树。树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
6、字典树
Trie树,即字典树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
前缀树的3个基本性质:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
使用场景:
AVL树: 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。
红黑树: 平衡二叉树,广泛用在C++的STL中。如map和set都是用红黑树实现的。
B/B+树: 用在磁盘文件组织 数据索引和数据库索引。
Trie树(字典树): 用在统计和排序大量字符串,如自动机。
哈夫曼树: 哈夫曼编码是哈夫曼树的一个应用。在数字通信中,经常需要将传送的文字转换成由二进制字符0、1组成的二进制串,这一过程被称为编码。在传送电文时,总是希望电文代码尽可能短,采用哈夫曼编码构造的电文的总长最短。