NOIP2020

T1：排水系统 

题意：n 个排水节点（1 ... n），m 个接水口（1 ... m），0 个排水管道的为出水口。

输入样例：
5 1
3 2 3 5
2 4 5
2 5 4
0
0
输出样例：
1 3
2 3
画出样例数据当中的示意图，如下图所示：

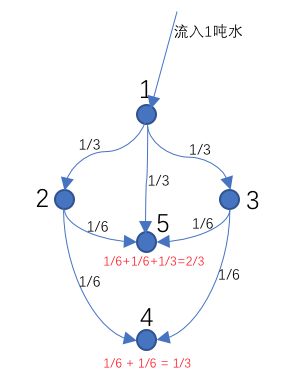
1、确定入水口：根据题意可知，有m个入水口，那么具体的口是（1，2，... ，m）

2、确定出水口：根据题意可知，在输入数据当中，如果没有排出管道连到其他节点，那么即为出水口。根据输入为0的时候，用一个数组标记即可。

3、在模拟流到其他节点的时候，怎么恰当的表示数据？肯定不能每次都用小数算出来，这样会有数精度的损失。那么根据流出管道的数量size，只要每次乘以一个size，即可得分流到该节点的水流量。这时候分为两种情况：

1）假如是中间节点的话，那么只要不停的乘以这个size得到当前节点分母的大小，分子就一直都是1。然后加入队列。

2）如果是最终流出节点的话，那么就每次从队列里取出一个节点之后，若该节点的下一个节点就是流出节点的话，那么加上第一个流入该节点的流量；若后面还有节点流到该流出节点的话，那么就累加起来：得到最终的ans_x[i], ans_y[i]。两个分数相加的简单方法就是先用最大公约数求出最小公倍数，然后最小公倍数除以各自的分母即为两个分子要乘的积。加起来之后再用最大公约数约一下分得到最简分数。

因为本题的数据范围是：可能会到10-26，所以即使是long long也过不了。可以用double，然后对应的gcd改成 a - floor(a / b) * b即可。

 AC代码：

#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1e5 + 10;
const double eps = 1e-18;
#define int long long
int n, m;
double x[N], y[N], G;
struct Node{
    int num, val;
}b[N];
bool st[N];
vector<int> a[N];
queue<Node> q;

double gcd(double a, double b)
{
    if(a < b) swap(a, b);
    if(b < eps) return a;
    return gcd(b, a - floor(a / b) * b);
}

void bfs()
{
    while(q.size())
    {
        Node t = q.front(); q.pop();
        int Size = (int)a[t.num].size();
        t.val *= Size;
        for(int i = 0; i < Size; i ++)
        {
            int Y = a[t.num][i];
            if(st[Y])
            {
                if(!x[Y] || !y[Y])
                {
                    x[Y] = 1; y[Y] = t.val;
                    continue;
                }
                double g1 = gcd(y[Y], t.val), g = y[Y] / g1 * t.val;
                x[Y] = g / y[Y] * x[Y] + g / t.val * 1;
                y[Y] = g;
                G = gcd(x[Y], y[Y]);
                x[Y] /= G;
                y[Y] /= G;
                continue;
            }
            q.push({Y, t.val});
        }
    }
}

signed main()
{
    scanf("%lld%lld", &n, &m);
    for(int i = 1; i <= n; i ++)
    {
        int T; scanf("%lld", &T);
        if(!T) { st[i] = 1; continue; }
        while(T --)
        {
            int x; scanf("%lld", &x);
            a[i].push_back(x);
        }
    }
    for(int i = 1; i <= m; i ++)
    {
        Node t; t.num = i; t.val = 1;
        q.push(t);
    }
    bfs();
    for(int i = 1; i <= n; i ++)
        if(st[i])
            printf("%.0lf %.0lf\n", x[i], y[i]);
}