树形DP

　　通过上一节的学习，应该对动态规划在树形结构上的实现方式有了初步的认识。给定一棵有N个节点的树（通常是无根树，也就是有N - 1条无向边），我们可以任选一个结点为根节点，从而定义出每个节点的深度和每棵子树的根。在树上设计动态规划算法时，一般就以节点从深到浅（子树从小到大）的顺序作为DP的“阶段”。DP的状态表示中，第一维通常是节点编号（代表以该节点为根的子树）。大多数时候，我们采用递归的方式实现树形动态规划。对于每个节点 x，先递归在它的每个子节点上进行DP，在回溯时，从子节点向节点 x进行状态转移。

1、基本概念

　　树形DP称为树形动态规划，顾名思义，就是在“树”的结构上做动态规划，通过有限次地遍历树，记录相关信息，以求解问题。通常，动态规划都是线性的或者是建立在图上的，线性动态规划的顺序有两种方向：即向前和向后，相应的状态转移方程有两种，即顺推与逆推，而树形动态规划是建立在树上的，树中的父子关系天然就是个递归（子问题）结构，所以也相应的有两个方向。

1. 叶 -> 根，即根的子节点传递有用的信息给根，之后由根得出最优解的过程。这种方式DP的题目应用比较多。
2. 根 -> 叶，即需要取所有点作为一次根节点进行求值，此时父节点得到了整棵树的信息，只需要去除这个儿子的PD值的影响，然后再转移给这个儿子，这样就能达到根 -> 叶的顺序。

　　动态规划的顺序：一般按照后序遍历的顺序，即处理完儿子再处理当前结点，才符合树的子节点的性质。

　　实现方式：树形DP是通过记忆化搜索实现的，因此采用的是递归方式。

　　时间复杂度：树形动态规划的时间复杂度基本上是O(n)；若有附加维m，则是O(n * m)。

　　

2、经典问题

1. 树的重心

　　　　对于一棵n个节点的无根树，找到一个点，使得把树变成以该点为根的有根树时，最大子树的结点数最小。换句话说，删除这个点后最大连通块的结点数最小，那么这个点就是树的重心。

　　　　解法：任选一个结点为根，把无根树变成有根树，然后设 f[i] 表示以 i 为根的子树的结点个数。不难发现 f[i] = +1。程序实现思路：只需要一次DFS，在无根树转有根树的同时计算即可。其实在删除结点i后，最大的连通块有多少个结点呢？结点i的子树中最大的有max{f[j]}个结点，i的“上方子树”中有 n - f[i] 个结点，在动态规划中就可以根据定义顺便找出树的重心了。

 

Acwing 846 树的重心

给定一颗树，树中包含n个结点（编号1~n）和n-1条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数n，表示树的结点数。

接下来n-1行，每行包含两个整数a和b，表示点a和点b之间存在一条边。

输出格式

输出一个整数m，表示重心的所有的子树中最大的子树的结点数目。

数据范围

1≤n≤10^5

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010, M = 2 * N;
int n, ans = N;
int h[N], e[M], ne[M], idx;//n个单链表的头h[N];
bool st[N];
void insert(int a, int b)//插入以a为起点指向b的邻接表，插在a指向链表的开始位置h[a]
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u)
{
    st[u] = true;
    int sum = 1, res = 0;//sum子树节点总数，初始化为根节点自己一个，res表示剩下连通块的大小，即所求
    for(int i = h[u]; i != -1;i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            int s = dfs(j);//以u为根节点子树的大小
            res = max(s, res);//每求得一个子树的大小，放入预定的最小池子里面
            sum += s;//把u的每个子树的大小加到s里面，得到的就是u为根的子树的大小，剩下的就是: n - s
        }
    }
    res = max(res, n - sum);//先求得去掉某一个数 剩余连通块的最大值
    
    ans = min(ans, res);//去掉n个数每一个数之后所剩连通块最大值的最小。
    
    return sum;
}
int main()
{
    memset(h, - 1, sizeof h);
    cin>>n;
    for(int i = 0;i<n-1;i++)
    {
        int a,b;
        cin>>a>>b;
        insert(a, b), insert(b,a);//无向边，需要加入b->a, a->b。
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

　　2、树的最长路径

　　　　给定一棵 n 个结点的边带权的树，找到一条最长路径。换句话说，要找到两个点，使得它们的距离最远，它们之间的路径就是树的最长路径。

　　　　解法：一棵有根树的最长链，可能出现两种情况：1）从最下面的叶子结点到根节点。2）从一个叶子结点到另外一个叶子结点。

　　　　要解决这个问题，我们只需要求出以每个结点为根的子树中的最长链，取其中的最大值即为该树的最长链。

　　　　对于每个结点我们都要记录两个值：d1[i]表示以 i 为根的子树中，i 到叶子结点的距离最大值；d2[i]表示以 i 为根的子树中，除距离最大值所在子树，i 到叶子结点的距离最大值（也就是次大值）；　

　　令 j 是 i 的儿子。则：

　　1）d1[j] + dist[i][j] > d1[i]，则 d2[i] = d1[i]; d1[i] = d1[j] + dist[i][j];

　　2）否则，若d1[j] + dist[i][j] > d2[i]，则 d2[i] = d1[j] + dist[i][j];

　　最后扫描所有的结点，找最大的d1[i] + d2[i]的值。

 

 Acwing 1072 树的最长路径：

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

现在请你找到树中的一条最长路径。

换句话说，要找到一条路径，使得使得路径两端的点的距离最远。

注意：路径中可以只包含一个点。

输入格式

第一行包含整数 n。

接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。

输出格式

输出一个整数，表示树的最长路径的长度。

数据范围

1≤n≤10000,
1≤ai,bi≤n,
−10^5≤ci≤10^5

输入样例：

6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7

输出样例：

22

代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 10010, M = N * 2;
int h[N], e[M], w[M], ne[M], idx, ans;
void add(int a, int b, int c)
{
    w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int dfs(int u, int father)
{
    int dist = 0;
    int d1 = 0, d2 = 0;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(j == father) continue;
        int d = dfs(j, u) + w[i];
        dist = max(dist, d);
        
        if(d > d1) d2 = d1, d1 = d;
        else if(d > d2) d2 = d;
    }
    
    ans = max(ans, d1 + d2);
    
    return dist;
}

int main()
{
    int n;
    cin>>n;
    
    memset(h, -1, sizeof h);
    for(int i = 0; i < n - 1;i++)
    {
        int a, b, c;
        cin>>a>>b>>c;
        add(a, b, c), add(b, a, c);
    }
    
    dfs(1, -1);
    
    cout<<ans<<endl;
}

　　3、树的中心问题

　　　　给出一棵边带权的树，求树中的点，使得此点到树中的其他结点的最远距离最近。

　　　　分析：从任意一点 i 出发的最长路径的可能形态有两种。

　　　　1）从 i 点向上出发，即终点不在以 i 为根的子树中的最长路径长度为 u[i]；

　　　　2）从 i 点出发向下，即终点在以 i 为根的子树中的最长路径长度为 d1[i]。

　　　　这里的关键是如何计算 u[i]。i 点向上的路径必经过（i, prt[i])，而 i 点的父结点 prt[i] 又引出了两条路径：一条是prt[i] 向上的最长路径，其长度为 u[prt[i]]；另一条是 prt[i] 向下的路径，该路径不能途径 i 点，否则会产生重复计算。

　　　　设 d1[i] 表示以 i 为根的子树中，i 到叶子结点的距离最大值。

　　　　d2[i] 表示以 i 为根的子树中，i 到叶子结点的距离次大值；

　　　　分别用 c1[i] 和 c2[i] 记录 d1[i], d2[i] 是从哪个子树更新来的。

　　　　u[i] 表示出了以 i 为根的子树中的叶子结点外，其他的叶子结点到 i 的最大值。

　　　　1）首先，一遍树形DP算出 d1, d2, c1, c2。令 j 是 i 的儿子，则：

　　　　　　1. 若 d1[j] + dist[i][j] > d1[i]，则 d2[i] = d1[i], d1[i] = d1[j] + dist[i][j];

　　　　　　2. 否则，若 d1[j] + dist[i][j] > d2[i]，则 d2[i] = d1[j] + dist[i][j];

　　　　2) 设 prt[i] = x，

　　　　　　若 c1[x] != i 即 d1[x] 不从 i 更新而来的，那么 u[i] = max{d1[x], u[x]} + dist[x][i];

　　　　　　若 c1[x] = i 即 d1[x] 从 i 更新而来的，那么 u[i] = max{d2[x], u[x]} + dist[x][i];

　　　　3）最后在 n 个结点中找到最大值，即：

　　　　　　t[i] = max{u[i], d1[i]}(1 <= i <= n)

　　　　4) 树的中心：ans = min{t[i]}(1 <= i <= n)

Acwing 1073 树的中心

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

输入格式

第一行包含整数 n。

接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。

输出格式

输出一个整数，表示所求点到树中其他结点的最远距离。

数据范围

1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤10^5

输入样例：

5 
2 1 1 
3 2 1 
4 3 1 
5 1 1

输出样例：

2

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 10010, M = 2 * N, INF = 0x3f3f3f3f;
int n, h[N], w[M], ne[M], e[M];
int d1[N], d2[N], p1[N], p2[N], up[N], idx;
bool is_leaf[N];

void add(int a, int b, int c)
{
    w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs_d(int u, int father)
{
    d1[u] = d2[u] = -INF;
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(j == father) continue;
        int d = dfs_d(j, u) + w[i];
        if(d >= d1[u]) 
        {
            d2[u] = d1[u], d1[u] = d;
            p1[u] = j;   
        }
        else if(d >= d2[u]) d2[u] = d;
        
    }
    if(d1[u] == -INF) 
    {
        is_leaf[u] = true;   
        d1[u] = d2[u] = 0;
    }
    return d1[u];
}

void dfs_u(int u, int father)
{
    for(int i = h[u]; i != -1;i = ne[i])
    {
        int j = e[i];
        if(j == father) continue;
        if(p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
        else up[j] = max(up[u], d1[u]) + w[i];
        dfs_u(j, u);
    }
}

int main()
{
    cin>>n;
    memset(h, -1, sizeof h);
    for(int i = 0; i < n - 1;i++)
    {
        int a, b, c;
        cin>>a>>b>>c;
        add(a, b, c), add(b, a, c);
    }
    
    dfs_d(1, -1);
     dfs_u(1, -1);
     int res = d1[1];
    for(int i = 2;i <= n;i++) 
    {
        if(is_leaf[i]) res = min(res, up[i]);
        else res = min(res, max(d1[i], up[i]));
    }
    
    cout<<res<<endl;
    
}

 　　4、普通的树形DP

　　　　给定一棵树，现在要从中选出最少的点，使得所有的边至少有一个端点在选中的集合中。

　　　　分析：按照要求构建一棵树。对于这类最值问题，向来是用动态规划求解的。

　　　　点的取舍可以看成一种决策，那么状态就是在某个点取得时候或者不取的时候，以它为根的子树的最小代价。分别可以用f[j][1]和f[j][0]表示。

　　　　当这个点不取的时候，它的所有儿子都要取，所以f[i][0] = 。

 

　　　　当这个点要取得时候，它的所有儿子取不取无所谓，不过当然应该取最优的一种情况。所以

　　　　　　

 

 　　　　普通的树形DP中，常常会采用叶 -> 根的转移形式，根据父结点的状态确定子结点的状态，若子结点有多个，则需要一一枚举，将子结点（子树）的DP值合并。

AcWing 285. 没有上司的舞会

Ural大学有N名职员，编号为1~N。

他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。

每个职员有一个快乐指数，用整数 Hi 给出，其中 1≤i≤N。

现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。

在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

输入格式

第一行一个整数N。

接下来N行，第 i 行表示 i 号职员的快乐指数Hi。

接下来N-1行，每行输入一对整数L, K,表示K是L的直接上司。

输出格式

输出最大的快乐指数。

数据范围

1≤N≤6000,
−128≤Hi≤127

输入样例：

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

输出样例：

5

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 6010;

int n, happy[N], h[N], ne[N], e[N], idx;
int f[N][2];
bool has_father[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u)
{
    f[u][1] = happy[u];
    for(int i = h[u]; i!=-1;i = ne[i])
    {
        int j = e[i];
        dfs(j);
        
        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }
}
int main()
{
    cin>>n;
    for(int i = 1; i <= n; i++) cin>>happy[i];
    
    memset(h, -1, sizeof h);
    
    for(int i = 0; i < n - 1; i++)
    {
        int a, b;
        cin>>a>>b;
        has_father[a] = true;
        add(b, a);
    }
    
    int root = 1;
    while(has_father[root]) root++;
    
    dfs(root);
    
    cout<<max(f[root][0], f[root][1])<<endl;
}

　　　　树形DP还有一个重要拓展是与各类树形数据结构结合。例如，Trie上的DP、AC自动机上的DP、后缀自动机上的DP等。

　　　　有时我们的图可以不简单限制于树，在树的基础上进行简单扩展，也可以得到一些能用DP解决的例子，例如，环 + 外向树（在有根树的基础上，添加了一条某结点指向根的边的图）上的DP、仙人掌（每条边至多存在于一个简单环上）上的DP等。 

 

Acwing 1074 二叉苹果树

有一棵二叉苹果树，如果树枝有分叉，一定是分两叉，即没有只有一个儿子的节点。

这棵树共 N 个节点，编号为 1 至 N，树根编号一定为 1。

我们用一根树枝两端连接的节点编号描述一根树枝的位置。

一棵苹果树的树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

这里的保留是指最终与1号点连通。

输入格式

第一行包含两个整数 N 和 Q，分别表示树的节点数以及要保留的树枝数量。

接下来 N−1 行描述树枝信息，每行三个整数，前两个是它连接的节点的编号，第三个数是这根树枝上苹果数量。

输出格式

输出仅一行，表示最多能留住的苹果的数量。

数据范围

1≤Q<N≤100.
N≠1,
每根树枝上苹果不超过 30000 个。

输入样例：

5 2
1 3 1
1 4 10
2 3 20
3 5 20

输出样例：

21

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = 2 * N;

int n, m, h[N], e[M], ne[M], w[M], idx, f[N][N];

void add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

void dfs(int u, int father)
{
    for(int i = h[u]; ~i; i = ne[i])
    {
        if(e[i] == father) continue;
        dfs(e[i], u);
        for(int j = m; j >= 0; j--)
            for(int k = 0; k < j; k++)
                f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);
    }
}

int main()
{
    cin>>n>>m;
    memset(h, -1, sizeof(h));
    for(int i = 1; i < n; i ++)
    {
        int a, b, c;
        cin>>a>>b>>c;
        add(a, b, c), add(b, a, c);
    }
    
    dfs(1, -1);
    
    cout<<f[1][m]<<endl;
}

Acwing 323 战略游戏

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。

你能帮助他吗？

例如，下面的树：

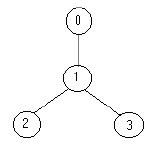
只需要放置1名士兵（在节点1处），就可观察到所有的边。

输入格式

输入包含多组测试数据，每组测试数据用以描述一棵树。

对于每组测试数据，第一行包含整数N，表示树的节点数目。

接下来N行，每行按如下方法描述一个节点。

节点编号：(子节点数目) 子节点 子节点 …

节点编号从0到N-1，每个节点的子节点数量均不超过10，每个边在输入数据中只出现一次。

输出格式

对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围

0<N≤1500输入样例：

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例：

1
2

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1510;
int n, h[N], e[N], ne[N], idx, f[N][2];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u)
{
    f[u][0] = 0;
    f[u][1] = 1;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        
        f[u][0] += f[j][1];
        f[u][1] += min(f[j][0], f[j][1]);
    }
}

int main()
{
    while(cin>>n)
    {
        memset(h, -1, sizeof h);
        idx = 0;
        memset(st, 0, sizeof st);
        for(int i = 0; i < n; i++)
        {
            int id, cnt;
            scanf("%d:(%d)", &id, &cnt);
            while(cnt--)
            {
                int ver;
                cin>>ver;
                add(id, ver);
                st[ver] = true;
            }
        }
        
        int root = 0;
        while(st[root]) root++;
        
        dfs(root);
        
        cout<<min(f[root][0], f[root][1])<<endl;
    }
}

Acwing 1077 皇宫看守

太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。

皇宫各个宫殿的分布，呈一棵树的形状，宫殿可视为树中结点，两个宫殿之间如果存在道路直接相连，则该道路视为树中的一条边。

已知，在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况，还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。

大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。

可是陆小凤手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。

帮助陆小凤布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

输入格式

输入中数据描述一棵树，描述如下：

第一行 n，表示树中结点的数目。

第二行至第 n+1 行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号 ii，在该宫殿安置侍卫所需的经费 k，该结点的子结点数 m，接下来 m 个数，分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。

对于一个 n 个结点的树，结点标号在 1 到 n 之间，且标号不重复。

输出格式

输出一个整数，表示最少的经费。

数据范围

1≤n≤1500

输入样例：

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例：

25

样例解释：

在2、3、4结点安排护卫，可以观察到全部宫殿，所需经费最少，为 16 + 5 + 4 = 25。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1510;
int n, w[N], e[N], ne[N], h[N], idx, f[N][3];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u)
{
    f[u][2] = w[u];
    for(int i = h[u];~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        f[u][0] += min(f[j][1], f[j][2]);
        f[u][2] += min(min(f[j][1], f[j][2]), f[j][0]);
    }
    
    f[u][1] = 1e9;
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        f[u][1] = min(f[u][1], f[j][2] + f[u][0] - min(f[j][1], f[j][2]));
    }
}

int main()
{
    cin>>n;
    memset(h, -1, sizeof h);
    
    for(int i = 1; i <= n; i++)
    {
        int id, cost, cnt;
        cin>>id>>cost>>cnt;
        w[id] = cost;
        while(cnt--)
        {
            int ver;
            cin>>ver;
            add(id, ver);
            st[ver] = true;
        }
    }
    int root = 1;
    while(st[root]) root++;

    dfs(root);
    cout<<min(f[root][1], f[root][2])<<endl;
}